2013.Термодинамика / Paskal / 2011_09_27 / 2011_09_27 / IMG_0046-108-109

- 108 -

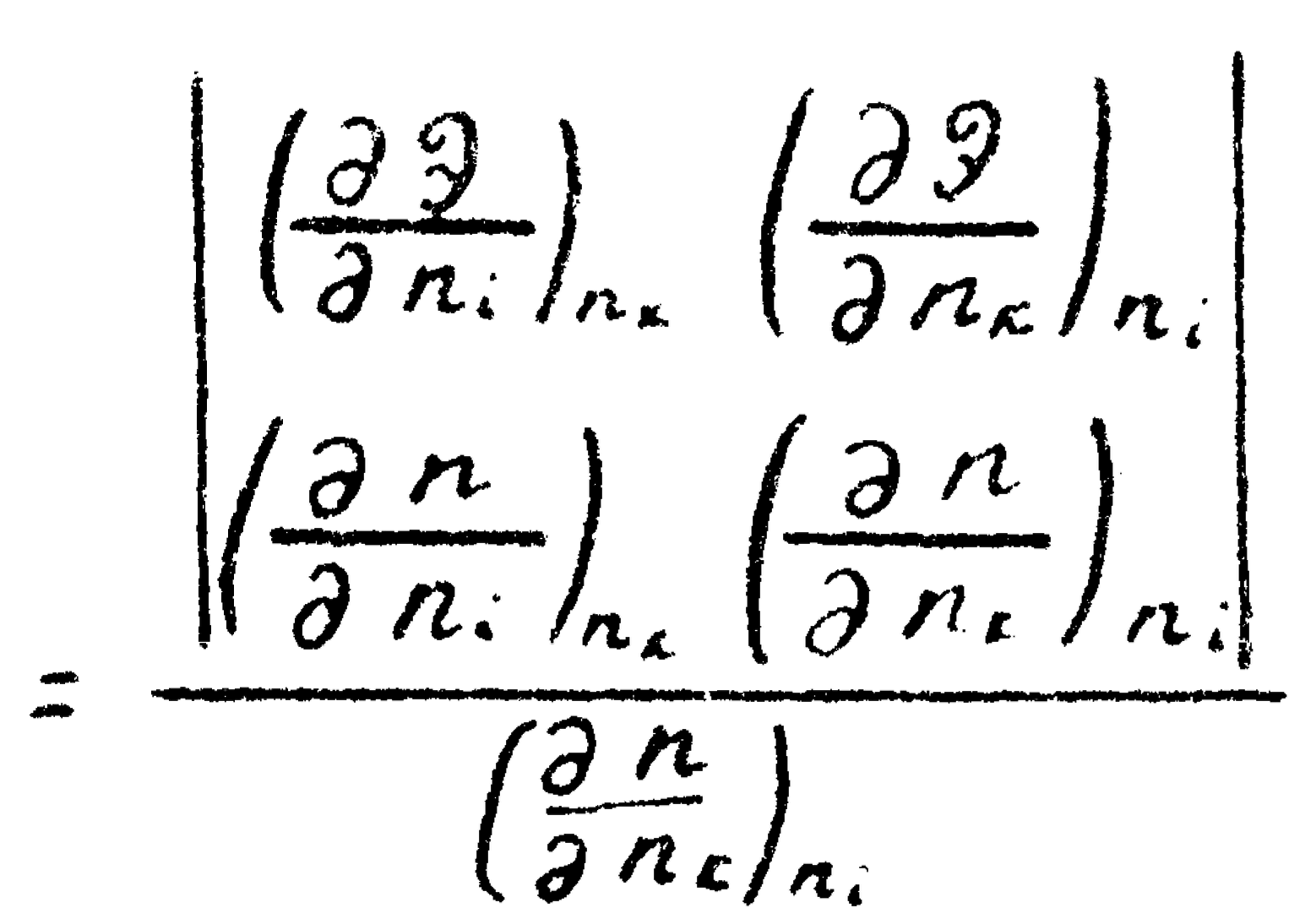
Легко видеть, что

Следовательно:

используя, получим

Рассматриваемая производная от равна разности м.п.ф. компонентов, участвующих в обмене.

Перейдём теперь вот дифференцировании по

к дифференцированию по . Для большей ясности верхним значком у производной второго типа будем обозначать, что дифференцирование проведено вдоль отрезка прямой, параллельной ребру симплекса, соединяющему вершины и

- 109 -

так как

Подставляя этот результат в , получим

или с учетом

Последняя формула связывает между собой производные двух типов Теперь из можно вывести формулу, эквивалентную

но выражающую м.п.ф. через производные второго типа от м.п.ф. Для этого умножим обе сторонына и просуммируем по

Откуда

или

М.п.ф.двухкомпонентной системы

В случае двухкомпонентной системы исчезает различие между производными двух типов, а формулы и 'становятся не только эквивалентными, но и тождественными. Действительно из

j

так как

у