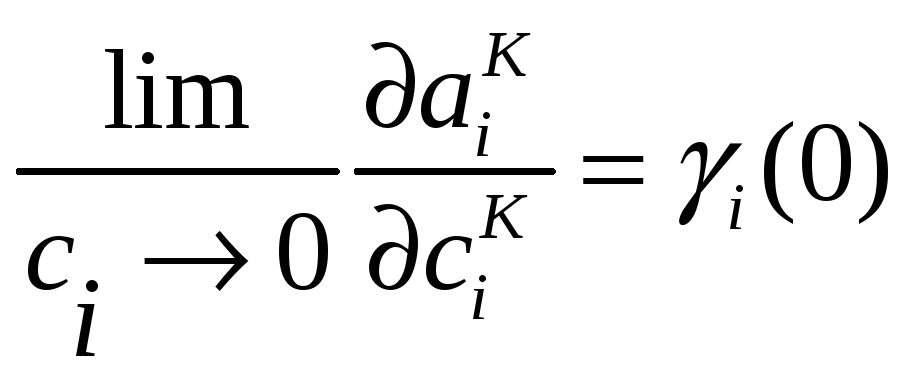2013.Термодинамика / Thermo-II / Лекция_II_6
.doc
В ряде случаев полезно еще одно обозначение
– коэффициент активности компонента
раствора
![]() .
.
![]() (29)
(29)
Легко видеть, что
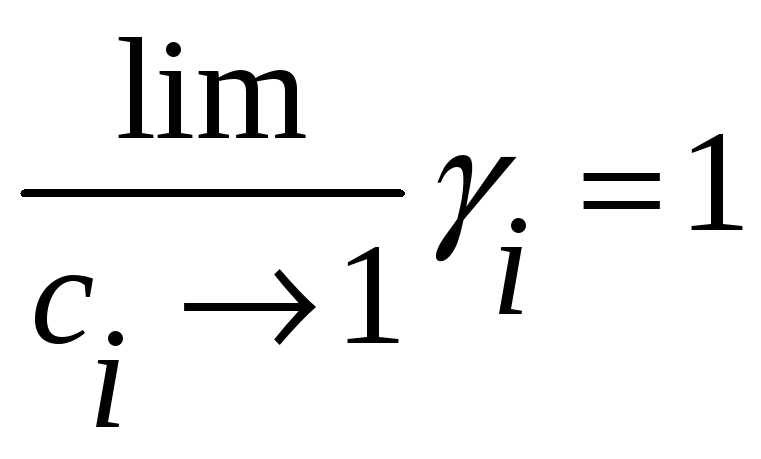 .
Но
.
Но
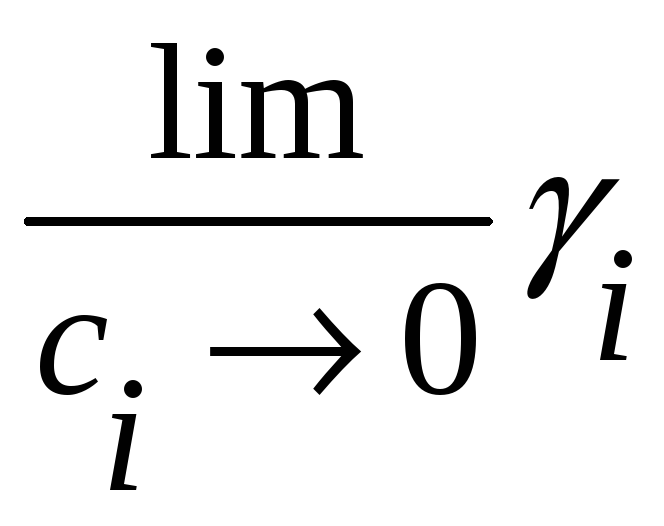 приводит к неопределенности, которую
мы проанализируем позже. Заметим только,
что этот lim величина
конечная. Химический потенциал через
коэффициент активности можно записать
приводит к неопределенности, которую
мы проанализируем позже. Заметим только,
что этот lim величина
конечная. Химический потенциал через
коэффициент активности можно записать
![]() .
.
Термодинамический потенциал Гиббса
![]()
Уравнение Гиббса-Дюгема приводится к
виду
![]()
Подставляя в (27)
![]() получим
получим
![]()
Вторая сумма равна
![]()
![]() (30)
(30)
Для идеальных растворов химический
потенциал
![]() ,
что в терминах введенных обозначений
приводит
,
что в терминах введенных обозначений
приводит
![]() ,
или
,
или
![]() ,
или
,
или
![]()
Идеальные растворы можно определить как растворы, для которых выполняется одна из этих записей.
В терминах активности условие диффузионной
устойчивости твердого раствора
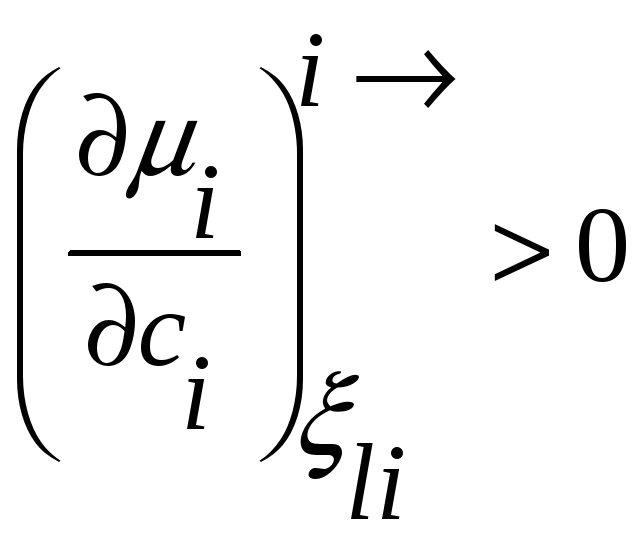 принимает вид
принимает вид
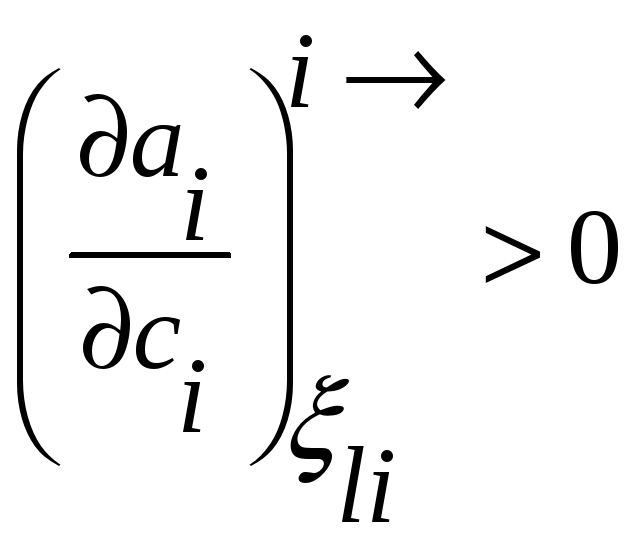 ,
т.е. в концентрационном интервале
устойчивости раствора активность растет
с повышением концентрации.
,
т.е. в концентрационном интервале
устойчивости раствора активность растет
с повышением концентрации.
Для коэффициента активности это условие
принимает вид
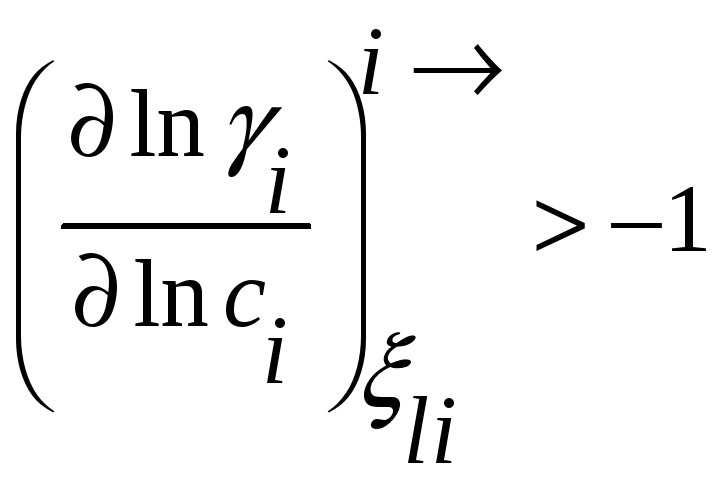
Соотношения между мольными парциальными
функциями
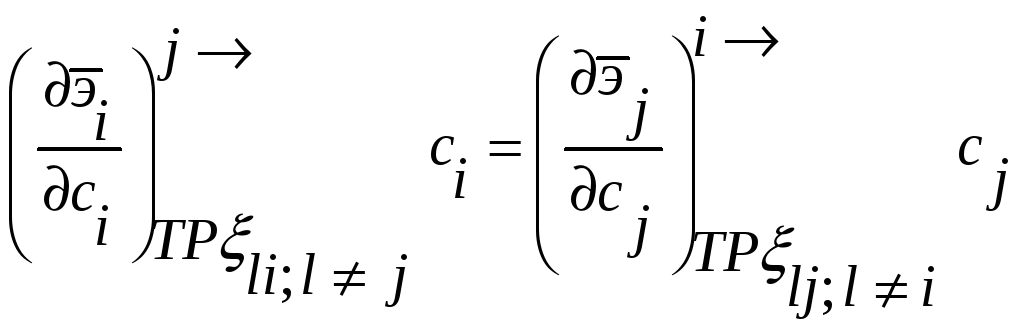 можно
переформулировать в виде соотношений
между активностями или коэффициентами
активности
можно
переформулировать в виде соотношений
между активностями или коэффициентами
активности
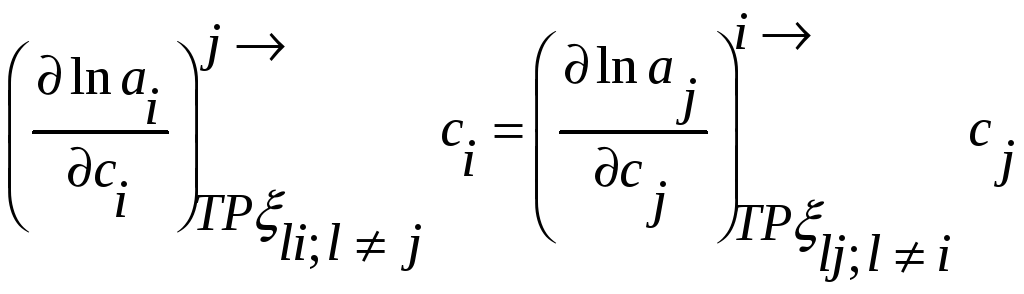 или для коэффициентов активности
или для коэффициентов активности
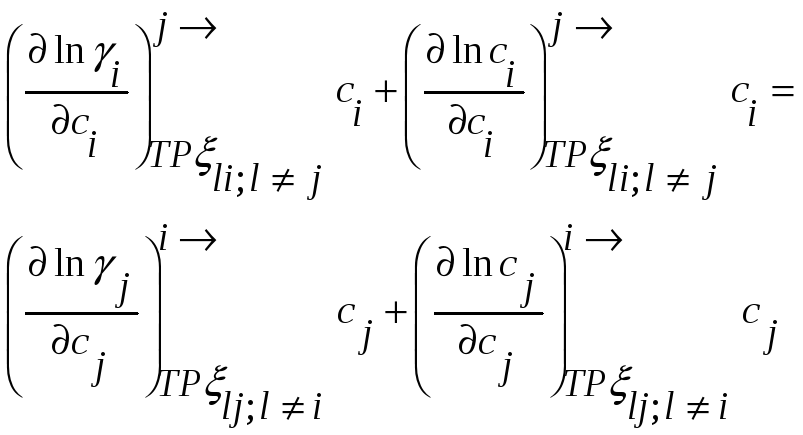 ,
но
,
но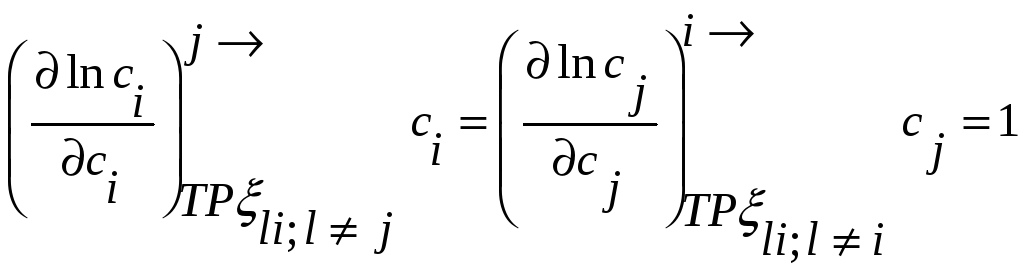
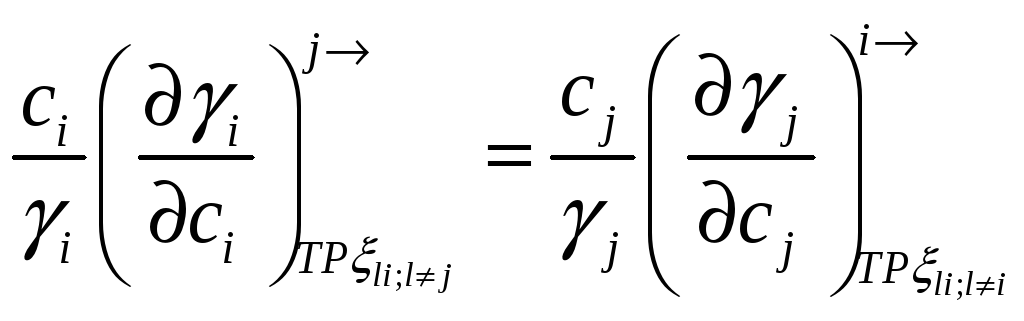
При помощи этих соотношений можно получить активность компонента j, если известна активность i-го компонента раствора. Если раствор идеален в отношении i-го компонента, то он идеален и в отношении j-го компонента раствора.
Коэффициент активности и мольные парциальные функции
Коэффициент активности может служить мерой отклонения раствора от идеальности. Из определения активности и коэффициента активности получим
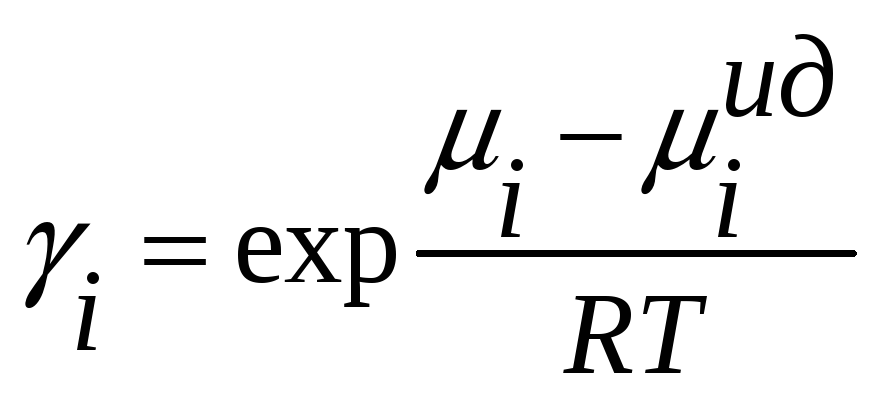 .
.
Из этого выражения видно, что реальные
растворы по своему поведению приближаются
к идеальным растворам при
![]() (если даже
(если даже
![]() ).
).
![]() получим
получим
![]() или
или
![]()
Для раствора с идеальной энтропией при
![]() ,
,
![]() и
коэффициент активности просто связан
с парциальной энтропией смешения
и
коэффициент активности просто связан
с парциальной энтропией смешения
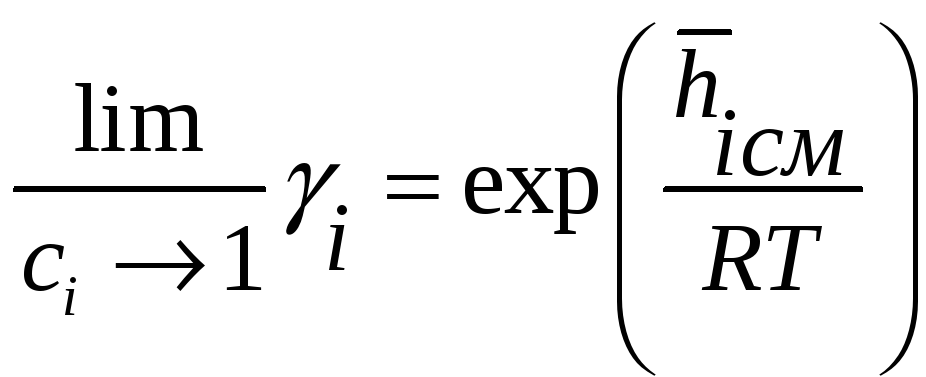
Положительные т отрицательные растворы
Положительными называются растворы,
для которых
![]() ,
,
![]() ,
,
![]() .
Отрицательными называются растворы
.
Отрицательными называются растворы
![]() ,
,
![]() ,
,
![]() .
Из
.
Из
![]() видно, что для положительных растворов
видно, что для положительных растворов
![]() ,
а для отрицательных
,
а для отрицательных
![]() ,
но обычно
,
но обычно
![]() ,
то понятие положительного твердого
раствора и эндотермического совпадают
Отрицательный раствор совпадает с
экзотермическим раствором.
,
то понятие положительного твердого
раствора и эндотермического совпадают
Отрицательный раствор совпадает с
экзотермическим раствором.
Закон Рауля
С помощью формализма Льюиса и общих формул термодинамики получим закон Рауля.
Рассмотрим равновесие двух растворов,
один из которых конденсированы (K),
другой газовый (Г). Условия фазового
равновесия двух растворов
![]()
Подставляя выражения химического
потенциала для газа и конденсированной
фазы через фугитивности получим
![]() (i=1,2,…,K),
где P – давление
равновесия конденсированного и газового
растворов (температура фиксирована).
Подставляя в это выражение
(i=1,2,…,K),
где P – давление
равновесия конденсированного и газового
растворов (температура фиксирована).
Подставляя в это выражение
![]() ,
получим
,
получим
![]()
![]() - фугитивность чистого компонента
раствора в конденсированном состоянии.
- фугитивность чистого компонента
раствора в конденсированном состоянии.
При данной фиксированной температуре и некотором давлении, вообще говоря, отличном от P , в равновесии находятся конденсированная и газовая фазы чистого i-го компонента.
![]() - это равновесие чистых
веществ в конденсированном и газовом
состоянии.
- это равновесие чистых
веществ в конденсированном и газовом
состоянии.
Фугитивности для конденсированного
чистого компонента
![]() и
и
![]() ,
для состояний с разным давлением, связаны
друг с другом соотношением
,
для состояний с разным давлением, связаны
друг с другом соотношением
![]() .
.
Для газовой фазы
![]()
Вычитая одно из другого получим выражение
![]() .
.
Если конденсированная фаза (кристалл
или жидкость) находится вдали от
критической точки, то
![]() и тогда
и тогда
![]()
Подставляя в последние выражение
значение для
![]() получим
получим
![]() ,
т.е. логарифм фугитивности чистого
компонента i в
конденсированном состоянии при давлении
P равен логарифму
фугитивности чистого компонента i
в газовой фазе при давлении
,
т.е. логарифм фугитивности чистого
компонента i в
конденсированном состоянии при давлении
P равен логарифму
фугитивности чистого компонента i
в газовой фазе при давлении
![]() .
Давление P –
давление равновесия конденсированного
и газового растворов, а
.
Давление P –
давление равновесия конденсированного
и газового растворов, а
![]() - давление равновесия чистого компонента
i в конденсированной
и газовой фазе.
- давление равновесия чистого компонента
i в конденсированной
и газовой фазе.
![]()
Подставляя это в
![]() получим
получим
![]()
Если конденсированный раствор идеален,
то
![]() ,
и
,
и
![]()
Фугитивность насыщенного пара i-го компонента над конденсированным раствором пропорциональна концентрации этого компонента в конденсированном растворе; Коэффициентом пропорциональности служит фугитивность насыщенного пара чистого i-го компонента над конденсированным чистым компонентом (температура фиксирована).
Если газовая фаза идеальна (что бывает
чаще в сравнении с конденсированным
состоянием), то
![]() и
и
![]() .
Подставляя эти два выражения в предыдущее
получим
.
Подставляя эти два выражения в предыдущее
получим
![]() ,
где
,
где
![]() - упругость пара i-го
компонента раствора (равновесное
парциальное давления i-го
компонента).
- упругость пара i-го
компонента раствора (равновесное
парциальное давления i-го
компонента).
![]() - упругость пара чистого i-го
компонента (давление равновесия газовой
и конденсированной фазы для чистого
компонента)
- упругость пара чистого i-го
компонента (давление равновесия газовой
и конденсированной фазы для чистого
компонента)
Это соотношение известно, как закон Рауля. Это эмпирическое правило было установлено в 1876г. Для двухкомпонентного раствора
![]() ,
,
![]() (31)
(31)
Понятие идеальный раствор возникло в
связи с законом Рауля. Это определение
совпадает с введенным ранее, если газовую
фазу рассматривать как идеальную и
![]() .
.
Запись
![]() имеет большую общность и называется
обобщенным законом Рауля. В случае
двухкомпонентного раствора, используя
закон Дальтона
имеет большую общность и называется
обобщенным законом Рауля. В случае
двухкомпонентного раствора, используя
закон Дальтона
![]() ,
и подставляя из закона Рауля
,
и подставляя из закона Рауля
![]() и
и
![]() ,
получим
,
получим
![]() .
В таком виде закон Рауля был записан
первоначально. График зависимости
.
В таком виде закон Рауля был записан
первоначально. График зависимости
![]() и
и
![]() от
от
![]() для двухкомпонентных систем представлен
на рис.1
для двухкомпонентных систем представлен
на рис.1
Л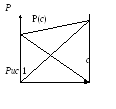 иния
P(c)
на этом графике представляет собой
нижнюю границу двухфазной области К+Г.
Верхняя границе полученными соотношениями
не определяется.
иния
P(c)
на этом графике представляет собой
нижнюю границу двухфазной области К+Г.
Верхняя границе полученными соотношениями
не определяется.
Отклонения от закона Рауля
Вскоре после открытия закона было,
обнаружено, что реальные системы
отклоняются в ту или сторону, т.е. для
некоторых систем
![]() .
Соответствующие конденсированные
растворы были определены как положительные.
Отрицательными назвали конденсированные
растворы, для которых
.
Соответствующие конденсированные
растворы были определены как положительные.
Отрицательными назвали конденсированные
растворы, для которых
![]() .
В рамках допущений, которые были сделаны
при выводе закона Рауля
.
В рамках допущений, которые были сделаны
при выводе закона Рауля
![]() ,
это соответствует для положительных
растворов условию
,
это соответствует для положительных
растворов условию![]() ,
а для отрицательных
,
а для отрицательных
![]() .
.
Если газовая фаза идеальна, а
конденсированная фаза не является
идеальным раствором, то имеет место
![]() или
или
![]() .
Эта формула подсказывает метод
непосредственного изменения активности
компонента конденсированного раствора.
Если газовая фаза не идеально, но
.
Эта формула подсказывает метод
непосредственного изменения активности
компонента конденсированного раствора.
Если газовая фаза не идеально, но
![]() ,
то имеет место более общее соотношение
,
то имеет место более общее соотношение
![]() (32)
(32)
Таким образом, для определения активности компонента конденсированного раствора достаточно определить фугитивности чистого газа и компонента газообразного раствора в равновесии с соответствующей конденсированной фазой.
Закон Рауля и Генри для предельно разбавленных растворов
Рауль эмпирически установил, что растворы
приближаются к идеальным при неограниченном
разбавлении. В пределе закон Рауля для
растворителя, то есть для компонента
концентрация, которого стремится к 1. В
некоторой окрестности
![]() (i=1,2) закон Рауля
выполняется с достаточной точностью.
Это означает, что
(i=1,2) закон Рауля
выполняется с достаточной точностью.
Это означает, что
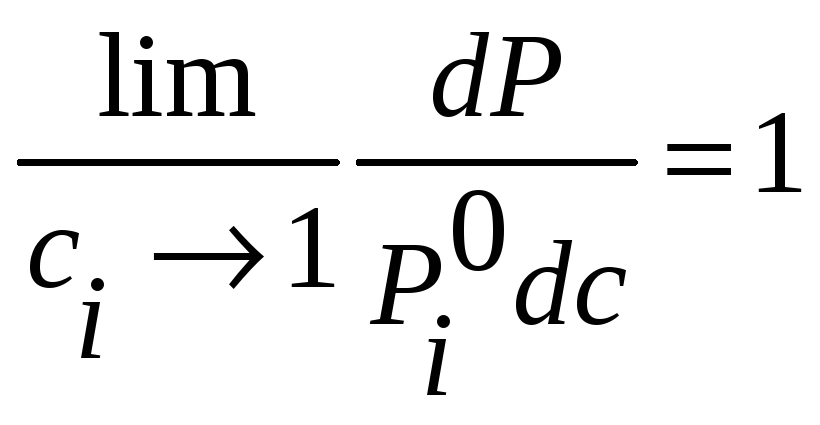 ,
(33)
т.е. линия
,
(33)
т.е. линия
![]() реальной системы при
реальной системы при
![]() имеет тот же наклон, что и прямая
имеет тот же наклон, что и прямая
![]() .
Обобщая это на случай неидеальной
газовой фазы запишем
.
Обобщая это на случай неидеальной
газовой фазы запишем
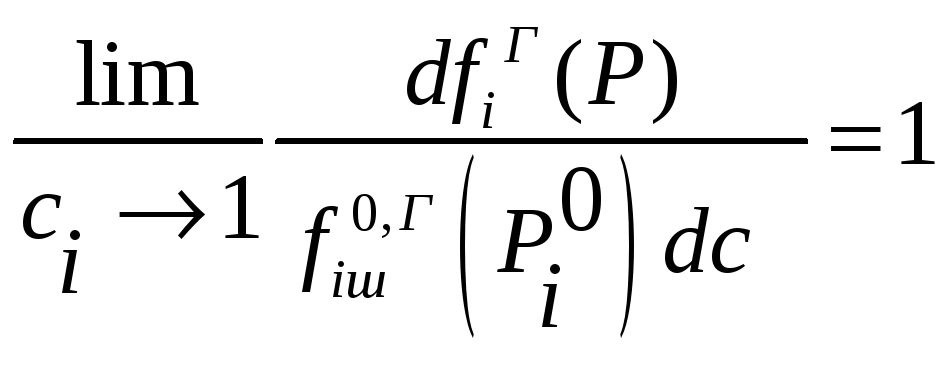
Если
![]() ,
то
,
то
![]() можно заменить на
можно заменить на
![]() и заменяя одновременно
и заменяя одновременно
![]() получим
получим
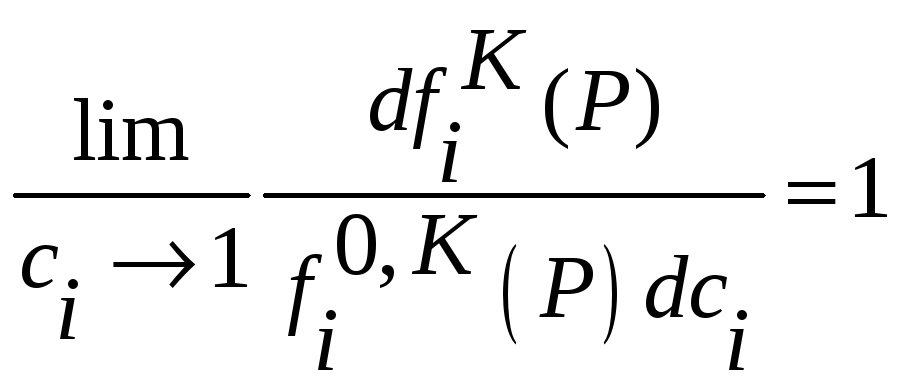 (34)
или
(34)
или
 ,
(35)
или
,
(35)
или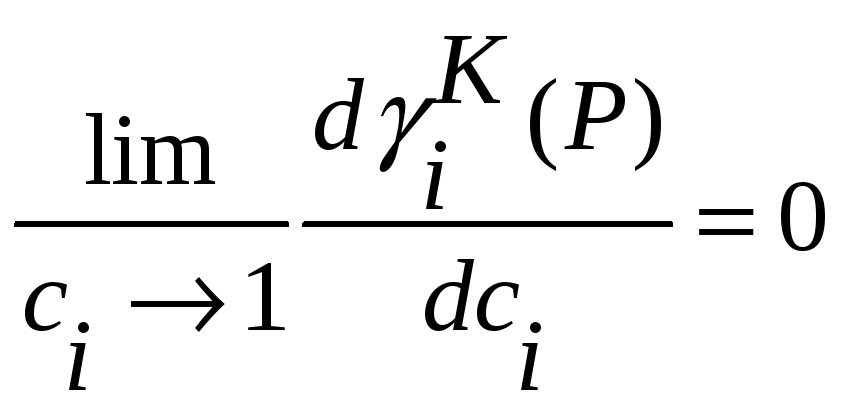 .
В достаточной близости от ci=1
c
достаточной точность выполняется
условие идеальности
.
В достаточной близости от ci=1
c
достаточной точность выполняется
условие идеальности
![]() или
или
![]()
Закон Генри
Эмпирически было установлено, что
поведение растворенного компонента в
двухфазной системе (Г+K)
подчиняется следующему правилу,
известному как закон Генри:
![]() (36)
(36)
при
![]() ,
где
,
где
![]() - некоторая величина, характеризующая
при данных T и
P систему и не
зависящая от
- некоторая величина, характеризующая
при данных T и
P систему и не
зависящая от
![]() (но, вообще говоря, зависящая
(но, вообще говоря, зависящая
![]() ).
).
Закон Рауля можно рассматривать как
частный случай закона Генри, соответствующий
![]() .
Закон Генри можно записать и виде
.
Закон Генри можно записать и виде
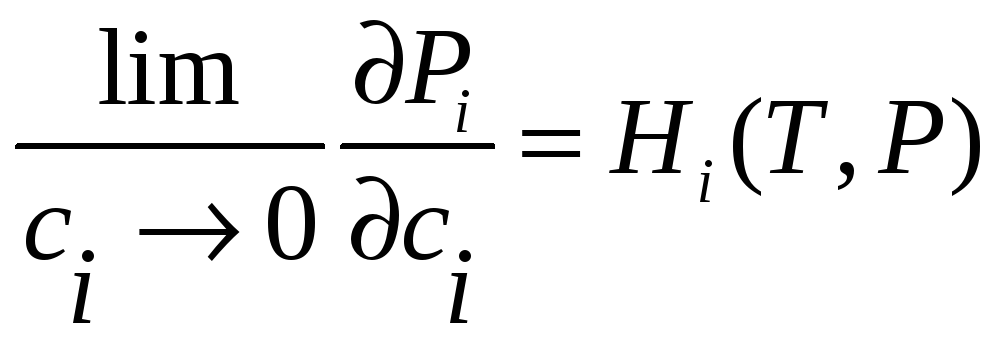 .
(37)
.
(37)
Генри получил этот закон для двухкомпонентной
системы:
![]() ;
;
![]() .
(38)
.
(38)
Более точная запись этого закона для двухкомпонентной системы:
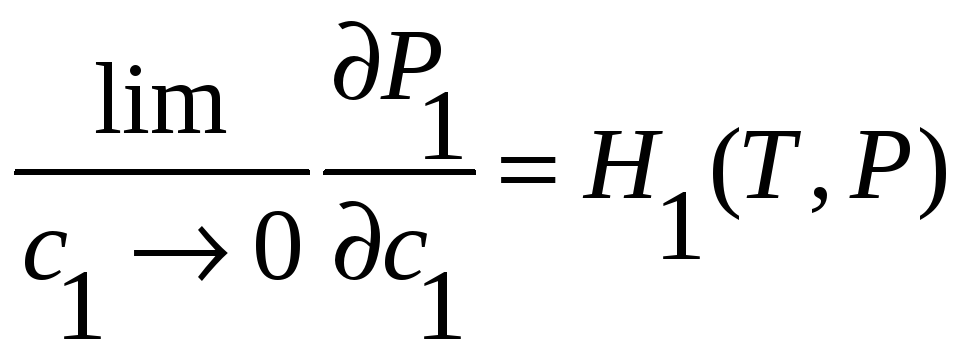 ;
;
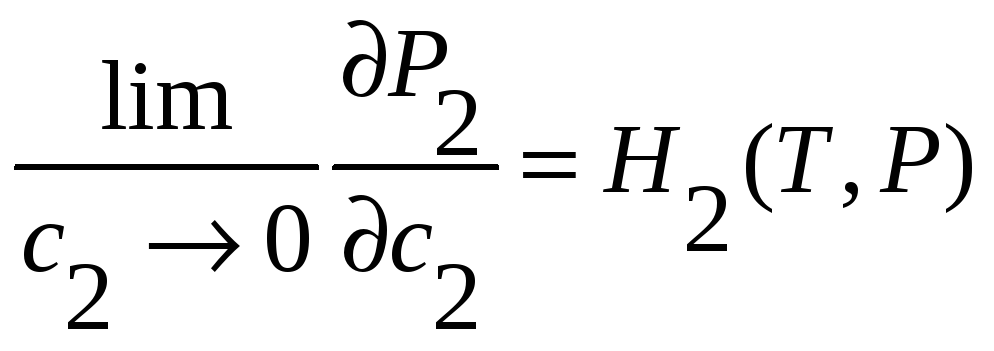 .
(39)
.
(39)
Это означает, что на графике
![]() с достаточной точностью выполняется
пропорциональность
с достаточной точностью выполняется
пропорциональность
![]() ;
кривая
;
кривая
![]() приближается к некоторой прямой,
отличной, вообще говоря, от прямой
приближается к некоторой прямой,
отличной, вообще говоря, от прямой
![]() ,
изображающей закон Рауля. Очевидно, что
для положительных растворов
,
изображающей закон Рауля. Очевидно, что
для положительных растворов
![]() ,
а для отрицательных -
,
а для отрицательных -
![]() .
Как показывает эксперимент с повышением
температуры
.
Как показывает эксперимент с повышением
температуры
![]() приближается
к
приближается
к
![]() сверху
(для положительных растворов и снизу
для отрицательных растворов).
сверху
(для положительных растворов и снизу
для отрицательных растворов).
Закон Генри (36) можно записать в виде
![]()
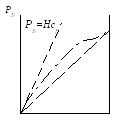
 ,
обобщая его на случай неидеальной
газовой фазы или в равноценной записи
,
обобщая его на случай неидеальной
газовой фазы или в равноценной записи
![]() .
Используя определение активности
компонента
.
Используя определение активности
компонента
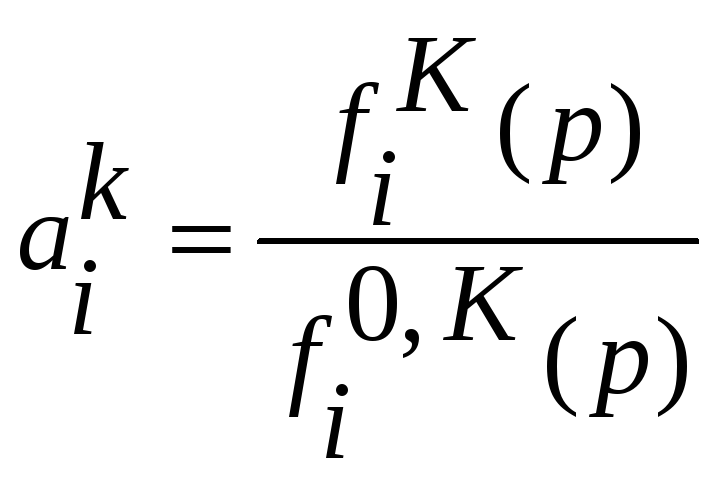 и предыдущую запись запишем закон Генри
в терминах активности компонента
и предыдущую запись запишем закон Генри
в терминах активности компонента
![]() ,
где
,
где
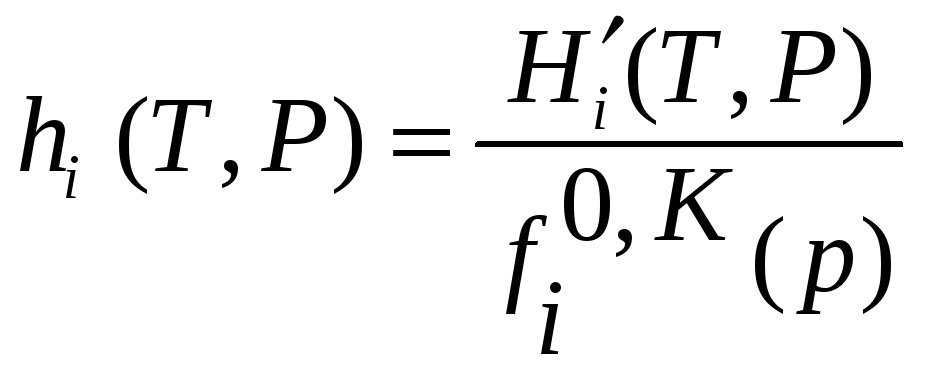 .
Запись закона в форме (37) в терминах
активности примет вид
.
Запись закона в форме (37) в терминах
активности примет вид
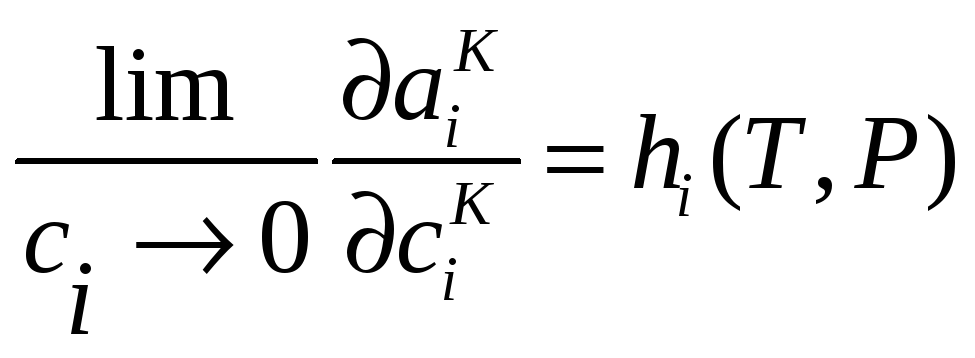 или с учетом
или с учетом
![]() и
и