7

Жоровков М.Ф. Термодинамика фазовых равновесий Лекция_II_4 591гр.

(1)

Формула (1) дает соотношения между производными первого и второго типов. Производные второго типа несколько более удобны. В частности для вывода полного дифференциала от мольной парциальной функции. Выберем c_k а качестве зависимой переменной и запишем дифференциал (ji,k) (2)

При T,P=const уравнение Гиббса- Дюгема подставив (2) в уравнение Гиббса- Дюгема запишем , или поскольку суммы конечны

Поскольку в полученном выражении стоят дифференциалы только независимых переменных, то уравнение Гиббса-Дюгема можно заменить системой уравнений (3)

Полный дифференциал через производные первого типа получится подстановкой (1) в (2)

Поскольку , то

Выбор k- го компонента совершенно произволен, лишь бы он не совпадал с компонентом, соответствующим вершине симплекса, из которой проведен луч, вдоль которого ведется дифференцирование. В данном выражении в производной типа дифференцирование ведется по компоненту i , находящемуся в вершине симплекса, из которой выходит луч, что следует из (ji), при фиксированном _j,k.во втором слагаемом мы сталкиваемся с точно такой же ситуацией. Поэтому второе слагаемой можно внести под знак суммы

(4)

Таким образом, выражение для полного дифференциала мольной парциальной функции через производные первого типа содержит k слагаемых, несмотря на то, что число независимых переменных равно k-1, т.е. из суммы не выбрасывается, слагаемые с i=j и i=k Просто при этом j и k в таком случае по-другому выбираются.

Например

Подставляя (1) в систему (3) получим систему из (k-1) уравнения (5)

i-1,2,…..,k-1. Во всех (k-1) уравнениях (5) в качестве k-го нужно выбирать один и тот же компонент.

Соотношения между производными от мольных парциальных функций, по концентрациям c_i.

Помимо уравнений(3) и (5) существуют и другие соотношения между мольными парциальными функциями. Рассмотрим для производных перового типа и некоторые их соотношения.

Соотношения между частными производными от мольных парциальных функций по концентрации c_i. Эти производные определяют характер зависимости от состава. Они используются при формулировке критерия устойчивости однородного твердого раствора.

Поскольку мы рассматриваем экстенсивные характеристики, являющиеся функциями состояния системы

Для функций состояния смешанные производные равны друг другу. (Поскольку для них существует полный дифференциал) Таким образом,

(6)

Соотношение (6) дает связь между производной от мольной п.ф. i –го компонента, полученного дифференцированием вдоль луча симплекса, проведенного из j- ой вершины и производной j – го компонента, полученной дифференцированием вдоль луча проведенного их i – вершины. Соотношение имеет место в фигуративной точке, лежащей на пересечении двух таких лучей. От производных по n_i,n_j можно перейти к производным поc_i,c_j. Подобно тому, как это мы делали раньше

В качестве j –го компонента в _l,j – удобно врать тот компонент для которого известна мольная парциальная функция.

Подставляя полученные выражения в (6) получим (7)

Однако, можно перейти от дифференцирования по n_i при n_ji=const перейти к дифференцированию по любой концентрации c_l в частности по c_j (а не обязательно c_i) при _l,j li. В любом случае это будут производные вдоль луча из I-ой вершины симплекса. При такой замене

Так как (n_i=const)

Подставляя в (6) получим

(8)

Химический потенциал.

Особую роль среди мольных парциальных функций имеет химический потенциал компонента раствора. Рассмотрим открытую многокомпонентную систему. Внутренняя энергия такой системы, как экстенсивная функция зависит от {n_i}ременных. Составим выражение баланса энергии, учитывая теплообмен механическую работу, массообмен: (9)

Первые два слагаемых соответствуют теплообмену Tds и механической работе –PdV. Сумма - соответствует изменению энергии за счет переноса вещества. Очевидно, что члены суммы входят в выражение баланса со знаком “+”.dU>0 при dn_i>0. Коэффициенты при этих членах принято называть химическими потенциалами. Подставляя левую часть равенства (9) в выражения U=F+TS, U=H-PV, U=+TS-PV

Получим еще три записи

Следовательно

Это четыре равноценных выражения, определяющих химический потенциал.

Последняя запись говорит, что химический потенциал представляет собой изобарно-изотермическую м.п. энергию Гиббса.

Для химического потенциала справедливы все соотношения, полученные ране для изобарно-изотермических м.п.ф.

Формула аддитивности .

Уравнение Гиббса-Дюгема В частности, при T,P=const При c_i=1 – химический потенциал i – го компонента равен мольной энергии Гиббса i – го чистого компонента ^_i.

Из формул для химического потенциала можно сказать, что он выступает, как изохорно-изоэнтропическая мольная парциальная функция и как изохорно-изоэнергетическая энергия Гельмгольца, и как изобарно-изоэнтропическая м.п. энтальпия.

Между мольными парциальными функциями существуют те же соотношения, что и между экстенсивными функциями:

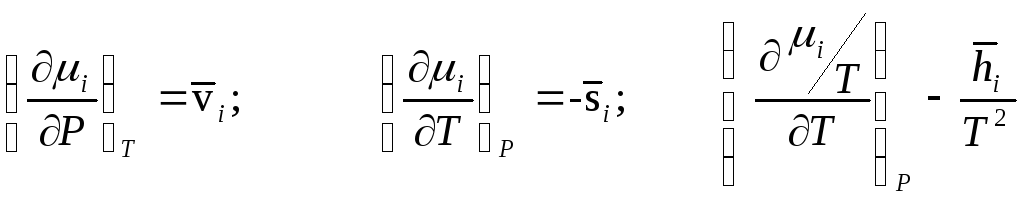
Для изохорно–изотермических мольных парциальных функций имеет место: .

Есть и другие соотношения. Доказательство можно осуществить воспользовавшись якобианами.

Стандартное состояние

Термодинамические функции в классической термодинамике определены с точностью до некоторой произвольной аддитивной величины. Абсолютными значениями могут обладать лишь изменения этих функций по отношению к некоторому выбранному уровню отсчета (стандартному состоянию). Невозможно выбрать единый для все систем уровень отсчета.

В качестве стандартного состояния выбирается обычно система, в которой каждый из компонентов присутствует в виде обособленной однокомпонентной фазы, при том же количестве вещества компонента, которое содержится в растворе и при тех же T и Р. При этом чистые компоненты находятся в том же фазовом состоянии, что и в растворе ( в том же агрегатном состоянии, с решеткой того же типа и теми же параметрами решетки), что и описываемый раствор.

Определение стандартного состояния не всегда просто определить на практике. В структуре раствора, очень часто, чистые вещества и не существуют. Будем рассматривать простой случай. Пусть чистые вещества существуют в той же структуре, что и в растворе.

Функции смешения

Экстенсивная функция стандартного состояния может быть записана , где - мольная функция чистого i–го компонента. Отсчитанная от этого уровня экстенсивная функция раствора и является функцией смешения Э_см: представляет собой изменение Э при образовании раствора. Ее называют функцией смешения или функцией растворения. Одновременно с функцией смешения введем мольную парциальную функцию смешения следующим образом:

. Подставим это выражение в Э_см. Получим , где и есть мольная парциальная функция смешения, то есть соответствующая мольная парциальная функция компонента раствора, отсчитываемая от того значения, которое она принимала при C_i=1.

Для системы можно ввести: энтальпию смешения H_см =H-H^○ внутреннюю энергию смешения U_см=U-U^○ энергию смешения Гиббса Φ_см=Φ-Φ^○ энтропию смешения S_см=S-S^○ изобарную теплоемкость смешения C_p,см=C_p-C^○_p.

Аналогично вводятся и мольные функции смешения. Для каждого компонента раствора можно ввести мольные парциальные функции смешения:

Энтальпию ;

Внутреннюю энергию ;

Энтропию; и т.д.

Очевидно, что между экстенсивными функциями смешения и мольными парциальными функциями смешения справедливы соотношения

; ,

и другие уравнения.