
telnov-machanika-and-TO
.pdf
|
|
|
|
|
|
|
|
pe |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|||||
|
1 e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, где a |
|
|
и b |
|
. |
(70.34) |
|||||||||||||
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
b2 |
1 e2 |
|
1 e2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2) |
e 1 (парабола) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
2 p x |
|
|
. |
|
|
|
|
(70.35) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
3) |
e 1 (гипербола) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
pe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|||||
|
e |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1, |
где a |
|
|
и b |
|
.(70.36) |
|||||||||||||||||||
|
|
|
|
|
a2 |
|
|
|
|
|
|
b2 |
|
|
e2 1 |
e2 1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
§ 71. Полеты в космос
Движение по круговой орбите.
При движении по круговой орбите вокруг Земли
mv2 |
= GMm |
v = |
GM . |
(71.1) |
2 |
r |
|
r |
|
Если спутник находится на низкой орбите около Земли, то r = RЗ и
v = |
GM R = |
gR = 7.9 км/с, |
(71.2) |
1 |
R2 З |
З |
|
|
З |
|
|
– это первая космическая скорость. Период обращения спутника на околоземной орбите
T = |
2pRЗ |
= 2p |
RЗ |
= 88 мин. . |
(71.3) |
|||
|
|
|
||||||
|
GM |
|
g |
|
||||
|
|
RЗ |
|
|
|
|
||
Для спутников на геостационарной орбите |
|
|||||||
T = |
2prГ |
= 1 сутки. |
(71.4) |
|||||
GM |
||||||||
|
|
|
|
|
|
|||
rГ
181
Отсюда rГ = 42.2 км и скорость и |
|
|
|
v |
= GM |
= 3.07 км/с. |
(71.5) |
Г |
rГ |
|
|
|
|
|
|
Вторая космическая скорость.
Для вылета на пределы Земли необходимо чтобы движение было инфинитно, а для этого, как было установлено ранее (в предыдущей лекции), необходимо
E = mv2 |
-GMm |
> 0 . |
(71.6) |
2 |
R |
|
|
|
З |
|
|
Заметим, что эта скорость не зависит от направления запуска ракеты. Минимальная скорость
v |
= |
2GM R = |
2gR = 11.2 км/с, |
(71.7) |
2 |
|
R2 З |
З |
|
|
|
З |
|
|
– это вторая космическая скорость.
Если скорость ракеты на поверхности Земли v , то скорость на бесконечности (r RЗ ) находится из закона сохранения энергии
|
|
mv¥2 |
= mv2 |
-GMm |
= mv2 |
- |
mv22 |
|
(71.8) |
|
2 |
|
|||||||
|
2 |
R |
2 |
2 |
|
|
|||
|
|
|
|
З |
|
|
|
|
|
отсюда |
v¥2 = v2 -(11.2)2, где скорости в км/с. |
(71.9) |
|||||||
Третья космическая скорость.
Найдем скорость, необходимую для полета за пределы Солнечной системы. Скорость Земли на орбите вокруг Солнца (аналог первой космической скорости)
v |
= |
GMC |
= 29.76 » 30 км/с. |
(71.10) |
|
||||
1C |
|
rЗ |
|
|
|
|
|
||
Здесь rЗ – радиус орбиты Земли вокруг Солнца, MC – масса Солнца.
182
Для полета на бесконечность с орбиты Земли в поле Солнца необходима вторая солнечная космическая скорость
v |
|
= |
2GMC |
= 2v |
= 42.1 км/с. |
(71.11) |
2C |
|
|||||
|
|
|
1С |
|
|
|
|
|
|
rЗ |
|
|
|
Т.е. вдобавок к орбитальной скорости Земли нужно иметь дополнительную скорость 42 30 12 км/с. Это значит, что на поверхности Земли ракета должна иметь скорость, см. (71.9)
v = |
(12)2 +(11.2)2 = 16.4 км/с. |
(71.12) |
|
Полет на Марс |
|
|
|
|
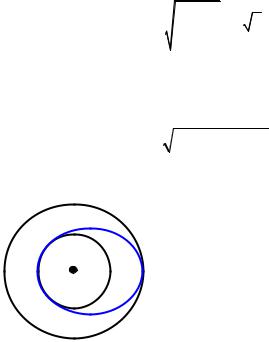
Самым экономичным полетом к Марсу яв- |
||
|
ляется полет, когда ракета стартует вдоль орби- |
||
|
тальной скорости Земли и далее, двигаясь по |
||
|
эллипсу, касается орбиты Марса, рис. 55. Дей- |
||
|
ствительно, |
согласно (70.8) |
полная энергия |
|
E GMm |
, где a - большая полуось. Отсюда |
|
|
2a |
|
|
|
начальная кинетическая энергия при старте с |
||
Рис. 55 |
орбиты Земли |
|
|
K |
0 |
= -GMm |
-U |
0 |
= -2GMm |
+GMm , |
(71.13) |
|
2a |
|
a |
rЗ |
|
||
|
|
|
|
|
и она уменьшается при уменьшении большой полуоси эллипса. Продолжительность полета (туда-обратно) находится из (70.19)
T 2 = |
4p2a3 |
= |
4p2(rЗ +rМ )3 |
. |
(71.14) |
|
|
||||
|
GMС |
|
8GMС |
|
|
Его можно выразить через периоды обращения Земли и Марса
T 2 |
= |
4p2rЗ3 |
, T 2 |
= |
4p2rM3 |
. |
(71.15), |
|
|
||||||
З |
|
GMС |
M |
|
GMC |
|
|
|
|
|
|
|
|||
В результате с учетом TЗ = 1 год, TM = 1.88 года , получаем
183
|
2 |
|
1 |
|
2/3 |
|
2/3 |
3 |
|
|
|
T |
|
= |
8 |
( З |
M |
) |
T = 1.42 |
года. |
(71.16) |
||
|
|
T |
|
+T |
|
|
|||||
Полная энергия ракеты при движении по эллипсу дается ф-лой (70.8)
GMC m |
|
|||
E = - |
|
|
. |
(71.17) |
r |
+r |
|||
|
З |
M |
|
|
Скорость ракеты на орбите Земли vЗ находится из сохранения энергии
|
|
|
|
|
|
|
|
mv2 |
|
GMC m GMC m |
, |
(71.18) |
|||||||||
|
|
|
|
E = |
|
|
З |
- |
|
|
|
|
= - |
|
|
||||||
|
|
|
|
2 |
|
|
|
r |
|
r |
+r |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
З |
|
|
З |
M |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
v |
З |
= |
2GMCrM |
|
= v |
|
|
|
|
|
rM |
|
|
» 42.1 0.78 = 32.7 км/с. |
(71.19) |
||||||
r (r +r ) |
2C |
|
r +r |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
З M |
З |
|
|
|
|
|
З |
|
|
M |
|
|
|
|
|
|
||
Поскольку имеется скорость орбитального движения Земли 29.76 км/с, то необходимая добавочная скорость 32.7 -29.76 » 2.95 км/с. Для этого стартовая скорость ракеты на поверхности Земли должна быть
(см. (71.9))
v = (2.95)2 +(11.2)2 = 11.6 км / с. |
(71.20) |
Это и есть искомая скорость ракеты для полета на Марс. Она лишь немного больше второй космической скорости.
Заметим, что формулу (71.19) можно легко получить не прибегая к общему решению движения по эллиптическим орбитам. В точках, где орбита ракеты касается орбит Земли и Марса скорость ракеты перпендикулярна радиусу. Законы сохранения момента импульса и энергии для этих двух точек
|
|
|
vЗrЗ = vMrM, |
|
|
|
(71.21) |
||||
v2 |
|
GM |
C |
|
v2 |
|
GM |
C |
, |
(71.22) |
|
З |
- |
|
|
= |
M |
- |
|
||||
2 |
|
r |
|
2 |
r |
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
З |
|
|
|
|
M |
|
|
|
откуда, сразу получаем для vЗ выражение, совпадающее с (71.19).
184

Долететь до Марса не так сложно, труднее вернуться. Вторая космическая скорость для Марса около 5 км/с (для Луны 2.375 км/с), так что стартовая масса посадочного модуля должна быть достаточно большая. Возможно, первые покорители Марса полетят в одну сторону. Сначала с помощью роботов построят жилище, завод по производству товаров жизненной необходимости, а затем полетят люди- «переселенцы» . Еще одна проблема—это очень высокая радиация во время полета и на поверхности Марса. Доза, получаемая во время полета, составляет порядка 100 бэр (1 Зиверт), что является предельно допустимой для людей. На поверхности Марса радиация примерно втрое выше, чем на орбитальной станции, но там хоть можно спрятаться.
Рассмотрим еще вопрос, как часто Земля и Марс имеют расположение удобное для полетов? Пусть З и wM -угловые скорости движения
Земли и Марса вокруг Солнца. Тогда в системе отсчета, вращающейся вместе с Землей, угловая скорость Марса w = wЗ - wM . Время взаимное расположение повторяется с периодом
T = |
|
|
2p |
|
= |
|
TЗTM |
|
= 2.14 года. |
(71.23) |
|
w |
З |
- w |
M |
T -T |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
M |
З |
|
|
|||
Нужно еще учесть, что орбита Марса имеет большой эксцентриситет. Минимальное расстояние до Солнца 207 млн. км, максимальное 249 млн. км. Если сильно экономить, то лететь нужно, когда Марс находится близко к Солнцу (меньше будет большая полуось орбиты), это порядка четверти всего времени. Такие очень удобные случаи будут повторяться через 2.14/0.25~8 лет.
Полет к Солнцу
Посмотрим, сколько времени займет полет к Солнцу и какая для этого нужна скорость. Полет к Меркурию близок к полету на Солнце, туда уже летал «Маринер-10» в 1974—1975 гг.
Оптимальная орбита для полета на Солнце — это сильно вытянутый эллипс, имеющий двойную полуось равную расстоянию до Солнца. С
учётом зависимости T 2 |
µa3 |
находим время полета к Солнцу |
|
|||
|
æ |
1 |
ö3/2 |
|
|
|
T = |
ç |
÷ |
T = 0.35 |
года. |
(71.24). |
|
ç |
|
÷ |
||||
|
ç |
2 |
÷ |
З |
|
|
|
è |
ø |
|
|
|
|
185

Скорость на орбите Земли должна быть нулевой, для этого нужно запустить ракету в сторону противоположную орбитальной скорости Земли со скоростью 30 км/с. Вдобавок, нужно выйти за пределы тяготения Земли. Необходимая для всего этого скорость
v = (30)2 +(11.2)2 = 32 км/с. |
(71.25) |
Это вдвое больше, чем третья космическая скорость (71.12), необходимая для покидания Солнечной системы.
§ 72 Средние потенциальные и кинетические энергии, теорема о вириале.
Начнем с кругового движения. При движении по круговой орбите в поле
U(r) = - |
a |
(72.1) |
|
rn |
|||
|
|
В природе чаще всего встречаются силы с n = 1 (электрическое и гравитационное взаимодействия), однако бывают и другие. Например, между нейтральными молекулами существуют силы Ван-дер-ваальса (диполь-дипольные взаимодействия) с n = 6 . Кинетическая энергия при движении по окружности находится из уравнения движения
dp |
= - |
¶U |
= -dU |
r |
, |
что дает |
mv2 |
= |
na |
(72.2) |
dt |
dr |
|
r |
rn+1 |
||||||
|
dr r |
|
|
|
|
|||||
Отсюда находим соотношения между кинетической, потенциальной и полной энергиями
K = |
mv2 |
= |
|
na |
= - |
n |
U, |
|
|
|||
2 |
|
2rn |
2 |
. |
(72.3) |
|||||||
|
|
|
|
|
|
|
|
|||||
E = K +U = n -2 K = (2 |
-n)U. |
|
||||||||||
|
|
|
|
|
|
n |
|
|
|
|
2 |
|
Например, для гравитационного поля, |
n = 1, |
|
|
|
|
|
||||||
K = - |
U |
, |
|
E = -K = |
U |
. |
|
(72.4) |
||||
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
||
для поля гармонического осциллятора (U = kr2 ), |
n = -2 , |
|
||||||||||
K =U, |
|
|
E = 2K = 2U. |
|
(72.5) |
|||||||
Пример. Пусть искусственный спутник Земли за много оборотов тормозится в верхних слоях атмосферы, при этом орбита остается при-
186

мерно круговой. Что происходит со скоростью? На первый взгляд, раз тормозится, то скорость уменьшается. Это было бы так, если торможение происходило на коротком участке орбиты, а при медленном торможении нужно учесть изменение радиуса орбиты. Торможение означает уменьшение полной энергии. Из (72.4) следует, что уменьшение полной энергии означает уменьшение потенциальной энергии (уменьшение радиуса орбиты) и увеличение кинетической энергии!
Рассмотрим теперь произвольное финитное движение системы частиц. Запишем уравнение движения для одной частицы
F = mv (72.6)
Помножим обе части на r и просуммируем по всем частицам
|
|
åFr = åm(vr). |
(72.7) |
||||
Перепишем, учитывая, что |
d |
(vr)= vr + vr |
|
||||
|
|
||||||
|
|
dt |
|
||||
åFr = |
d |
åm (vr)- åm(vr) = |
d |
åm (vr)-2K |
(72.8) |
||
dt |
dt |
||||||
Усредним это выражение по большому времени, много большему, чем характерные времена в системе ( t ~ r/v ). Среднее от функции f (t)
это
f (t) dt
f (t) |
|
0 |
|
, |
. |
(72.9) |
|
|
|||||
|
|
|
|
|
|
Для предпоследнего члена в (72.8) интеграл равен выражению, стоящему после знака производной. При финитном движении скорости и расстояния конечные, поэтому сумма в предпоследнем члене (72.8) есть некое конечное число S(t) , тогда среднее значение этого члена
S( ) S(0) стремится к нулю при . Отсюда
|
|
|
1 |
åFr |
(72.10) |
K = - |
|||||
|
|
|
2 |
|
|
Величина -21 åFr называется вириалом сил, действующих в систе-
ме, а выражение (72.10) называют теоремой о вириале (Клаузиус, 1870).
В данном выражении F – это сила, действующая на одну из частиц со стороны всех остальных, а r – радиус-вектор частицы. Суммирова-
187

ние производится по всем частицам, так что (72.10) представляет собой двойную сумму. Однако ранее мы убеждались, что все силы в системе можно разложить на парные взаимодействия, в которых пары силы имеют противоположные направления, а полная потенциальная энергия системы есть сумма энергий парных взаимодействий. Поэтому, для простоты, не умаляя общности, рассмотрим систему всего из двух частиц. Тогда
åFr = F21r2 + F12r1 = F(r2 - r1) = Fr = - |
¶U |
r |
r = - |
¶U r |
(72.11) |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
¶r r |
|
¶r |
|
|||
ПустьU = - |
a |
, |
тогда ¶U r = n |
a |
r = n |
a |
|
= -nU . |
(72.12) |
|||
|
rn+1 |
rn |
||||||||||
|
rn |
¶r |
|
|
|
|
|
|||||
Отсюда |
åFr = nU . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(72.13) |
|||
Подставляя в (72.10), получаем |
|
|
|
|
|
|
|
|
|
|||
|
|
|
K = -nU , |
|
|
|
|
|
|
(72.14) |
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
E K U n 2 K (2 n) U . |
|
(72.15) |
|||||||
|
|
|
n |
|
|
2 |
|
|
|
|
|
|
В итоге, мы получили соотношение между потенциальной и кинетической энергиями в системах частиц, совершающих финитные движения, где потенциальная энергия взаимодействия между частицами
U = -ran . Соотношение оказалось таким же, как и для круговых ор-
бит.
§ 73. Астрофизические следствия теоремы о вириале
Связь излучения с температурой и размером системы
Пусть есть некоторая туманность, которая светится, тем самым теряя энергии. Из (72.15) для гравитационного взаимодействия ( n 1) K = -E . Раз E убывает, значит, кинетическая энергия растет. Кине-
тическая энергия пропорциональна температуре, K = 23 kTN , (k - постоянная Больцмана), поэтому температура тоже растет. При этом
188
размер туманности уменьшается, поскольку E = U2 ~ -GMr 2 , умень-
шение E означает уменьшение r .
Если на Солнце отключить термоядерные реакции, то его температура начнет расти! Собственно так и происходит. Когда в звезде выгорает водород, она начинает уменьшаться в размерах, ее температура возрастает, и начинают гореть более тяжелые элементы (гелий и.т.д.). «Горением» здесь является синтез тяжелых элементов из легких.
Неустойчивость межгалактического газа
Однородный газ не может быть гравитационно-устойчивым поскольку, если брать всё большие размеры, то потенциальная энергия
шара пропорциональна U µ M 2 , а кинетическая энергия пропорциональна количеству молекул, т.е. K µ M . Для устойчивости же необ-
ходимо K = -U2 . Газовое скопление будет сжиматься, если (опускаем численные коэффициенты)
|
GM 2 |
|
|
|
|
3 |
|
|
|
(73.1). |
||
|
|
|
|
³ NkT ~ nR kT |
|
|
||||||
|
|
R |
|
|
||||||||
Полагая M ~ MH nR3 , n ~ 10-5 см-1– |
плотность |
межзвездного газа, |
||||||||||
T ~ 104 – характерная температура, находим, что газ неустойчив при |
||||||||||||
R > |
|
kT |
|
= |
10-16104 |
|
24 |
см. |
(73.2) |
|||
|
|
|
|
|
|
|
~ 10 |
|||||
|
|
|
2 |
-7 |
-5 -48 |
|||||||
|
GnMH |
10 10 10 |
|
|
|
|
||||||
Это есть характерное расстояние между галактиками.
§ 74. Влияние солнечной радиации на движение малых тел
Давление света
Пусть пылинка радиуса R и плотности r находится на некотором
расстоянии r от звезды массы M , излучающей во все стороны мощность P . При поглощении света на пылинку действует сила, направленная от звезды,
F |
= |
P |
pR2 = |
PR2 . |
(74.1) |
|
4pr2c |
||||||
rad |
|
|
4r2c |
|
189

Сила гравитационного притяжения |
|
||
F |
= GMm |
= GM 4prR3 . |
(74.2) |
g |
r2 |
3r2 |
|
Обе силы пропорциональны 1/r2 , так что, если одна из них больше
другой, то так будет на всех расстояниях. Пылинка будет удаляться от звезды при Frad > Fg , т.е. при
R > |
|
3 |
|
|
P |
(74.3) |
|
|
|
|
|
|
|
||
16p GM rc |
|
||||||
Для Солнца, P = 3.9 1033 эрг/с, |
M = 2 1033 . Полагая плотность пы- |
||||||
линки r = 3 г/см3 , и учитывая, |
что G = 6.67 10-8 |
см3г-1с-2 (система |
|||||
СГС), получаем |
|
|
|
|
|
|
|
R > 2 10-5 |
см. |
(74.4) |
|||||
Таким образом, солнечный свет выдувает из солнечной системы все мелкие пылинки.
Эффект Пойнтинга-Робертсона
Пусть небольшое тело движется по круговой орбите вокруг Солнца. Солнечный свет падает на тело, а затем эта энергия изотропно (в системе тела) испускается в пространство. При поглощении порции энер-
гии de масса тела увеличивается на dm = dce2 . Эта дополнительная масса приобретает скорость тела и импульс вдоль траектории движения dp = vdm = dce2 v (при этом общий импульс тела вдоль орбиты не
меняется, т.к. фотоны прилетают перпендикулярно траектории). Световое давление на тело вдоль радиуса приводит только к не-
большому уменьшению силы притяжения, которая остается пропор-
циональна 1/ r2 (см. предыдущую задачу), им можно пренебречь. Поскольку температура тела в среднем сохраняется, вся поглощен-
ная энергия излучается изотропно в пространство, унося с собой этот импульс, забранный его у тела. Следовательно, тело испытывает силу трения
F |
= dp |
= -de |
v |
= -PpR2 |
v |
, |
(74.5) |
|
|
||||||
тр |
dt |
dt c2 |
4pr2 c2 |
|
|
||
190
