
- •§1. Определение пространства .
- •§2. Ряд Фурье.
- •Ортонормированные системы в евклидовом пространстве.
- •2. Ортонормированные системы в k[] и k[a,b].
- •3. Определение ряда Фурье.
- •4. Замкнутые системы в евклидовых пространствах.
- •§3. Тригонометрический ряд Фурье.
- •1. Замкнутость тригонометрической системы.
- •2. Тригонометрическая система в пространстве интегрируемых функций.
- •3. Ряд Фурье по тригонометрической системе (3.2).
- •4.Тригонометрический ряд Фурье в пространстве .
- •5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.
- •Комплексная форма записи тригонометрического ряда Фурье.
- •§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
- •1. Свойства интегрируемых функций
- •2. Интегральное представление частичных сумм тригонометрического ряда Фурье
- •3. Необходимое и достаточное условие сходимости ряда Фурье в точке
- •4.Достаточные условия поточечной сходимости ряда Фурье.
- •5. Примеры.
Комплексная форма записи тригонометрического ряда Фурье.
Возьмем произвольную функцию
![]() .
Согласно теоремам (4.2) и (3.3) ее ряд Фурье
по системе (3.2) сходится к ней в среднем.
Существует более компактная комплексная
форма записи тригонометрического ряда
Фурье. Для ее получения выразим по
формулам Эйлера
.
Согласно теоремам (4.2) и (3.3) ее ряд Фурье
по системе (3.2) сходится к ней в среднем.
Существует более компактная комплексная
форма записи тригонометрического ряда
Фурье. Для ее получения выразим по
формулам Эйлера
![]()
![]() .
.
Рассмотрим ряд Фурье (5.3) функции
![]() и будем называтьn-й
частичной суммой ряда Фурье выражение
и будем называтьn-й
частичной суммой ряда Фурье выражение![]() ,
(35.3) где коэффициенты
,
(35.3) где коэффициенты![]() вычисляются по формулам (6.3).
вычисляются по формулам (6.3).
Выразив
![]() и
и![]() по формулам Эйлера и подставив их в
по формулам Эйлера и подставив их в![]() ,
получим:
,
получим:![]()
![]()
Если обозначить
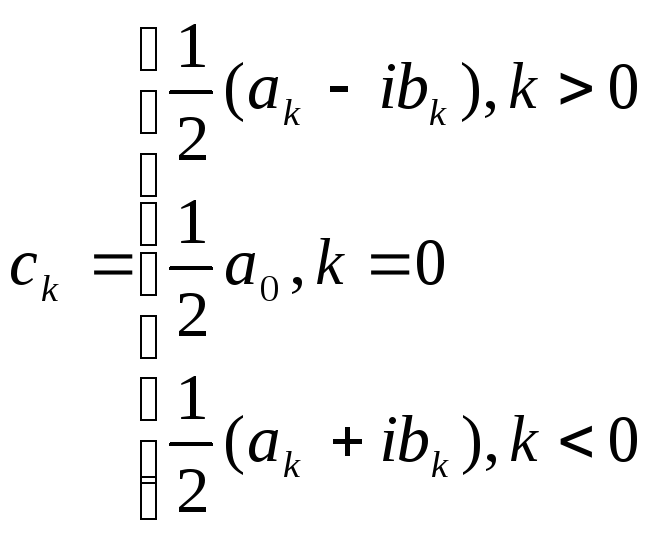
то
![]() перепишется так:
перепишется так:
![]() (36.3)
(36.3)
Легко видеть, что
![]() (37.3)
(37.3)
Тогда сам ряд Фурье можно переписать так:
![]() (38.3)
(38.3)
Следует только помнить, что суммирование ряда (38.3) понимается в смысле сходимости в среднем симметричных сумм (36.3).
Определение 2.3.Ряд (38.3) с
коэффициентами (37.3) называется рядом
Фурье функции![]() в
комплексной форме.
в
комплексной форме.
Отметим еще, что непосредственно из
определения
![]() вытекает
следующее свойство:
вытекает
следующее свойство:
![]() (39.3)
(39.3)
Легко видеть, что условие (39.3) является
необходимым и достаточным условием
того, что сумма
![]() принимает
только действительные значения
принимает
только действительные значения![]() .
.
Замечание 1.3.Точно также можно
показать, что ряд Фурье функции![]() по системе (4.2) в комплексной форме имеет
вид:
по системе (4.2) в комплексной форме имеет
вид:
![]() ,
где
,
где
![]()
Замечание 2.3Рассмотрим более широкий
класс функций, чем![]() .
Обозначим через
.
Обозначим через![]() множество
классов эквивалентных (то есть равных
почти всюду на
множество
классов эквивалентных (то есть равных
почти всюду на![]() )
функций, имеющих на
)
функций, имеющих на![]() не
более чем конечное число особых точек
и таких, что их квадрат модуля интегрируем
на
не
более чем конечное число особых точек
и таких, что их квадрат модуля интегрируем
на![]() по
Риману в собственном или несобственном
смысле. Очевидно, что
по
Риману в собственном или несобственном
смысле. Очевидно, что![]() .
Скалярное произведение в
.
Скалярное произведение в![]() также
определим формулой (5.1).
также
определим формулой (5.1).
Не трудно проверить, что все определения
и теоремы останутся в силе, если в
формулировках пространство
![]() заменить
на
заменить
на![]() .
В частности, справедлива теорема о том,
что система (4.2) замкнута в пространстве
.
В частности, справедлива теорема о том,
что система (4.2) замкнута в пространстве![]() .
.
§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
В предыдущем параграфе в теореме 3.3 и
следствии 2.3 доказана сходимость
тригонометрического ряда Фурье (9.3) в
среднем, то есть по норме пространства
I[-l,l].
При решении многих задач математической
физики с помощью рядов Фурье важную
роль играет вопрос о поточечной и
равномерной сходимости ряда Фурье, так
как он напрямую связан с вопросом
существования классического решения.
Известно, что для поточечной сходимости
ряда Фурье (а тем более равномерной)
недостаточно требовать только
непрерывности функции![]() .
В этом параграфе будут рассмотрены
дополнительные условия на функцию
.
В этом параграфе будут рассмотрены
дополнительные условия на функцию![]() ,
достаточные для поточечной и равномерной
сходимости тригонометрического ряда
Фурье. Но вначале докажем несколько
вспомогательных теорем и тождеств.
,
достаточные для поточечной и равномерной
сходимости тригонометрического ряда
Фурье. Но вначале докажем несколько
вспомогательных теорем и тождеств.
1. Свойства интегрируемых функций
Лемма 1.4.Предположим, что
Функция
 определена
и ограничена на промежутке
определена
и ограничена на промежутке ;
;

Тогда
![]()
Доказательство.
Доопределим
![]() ,
положив
,
положив![]() .
Из условия 1) следует, что существует
.
Из условия 1) следует, что существует![]() такая,
что
такая,
что![]()
![]() Проверим выполнение критерия
интегрируемости
Проверим выполнение критерия
интегрируемости![]() на
на![]() .
Для этого обозначим через
.
Для этого обозначим через
![]() ,
,![]() верхнюю и нижнюю сумму Дарбу функции
верхнюю и нижнюю сумму Дарбу функции![]() на отрезке
на отрезке![]() для данного разбиенияTсоответственно.
для данного разбиенияTсоответственно.
Возьмем
![]() .
Выберем точку
.
Выберем точку![]() так,
чтобы
так,
чтобы![]()
Из условия 2) следует, что существует
разбиение
![]() отрезка
отрезка![]() такое, что
такое, что![]() .
Обозначим через
.
Обозначим через![]() T-разбиение отрезка
[a,b]. Тогда
T-разбиение отрезка
[a,b]. Тогда![]() .
Критерий интегрируемости выполнен.
Лемма доказана.
.
Критерий интегрируемости выполнен.
Лемма доказана.
Лемма Римана. Если![]() ,
то
,
то
![]() (1.4)
(1.4)
![]() (2.4)
(2.4)
Доказательство.
Докажем предел (1.4). Сначала заметим, что
![]() (3.4)
(3.4)
Пусть Tразбиение [a,b]
точками![]() .
Обозначим
.
Обозначим![]() ,k=1,…,n.
Преобразуем
,k=1,…,n.
Преобразуем

Отсюда и (3.4), используя несложные оценки, получим
![]() (4.4)
(4.4)
Берем
![]() Так как
Так как
![]() то
существует разбиениеTтакое, что
то
существует разбиениеTтакое, что Зафиксируем
это разбиение. Обозначим через
Зафиксируем
это разбиение. Обозначим через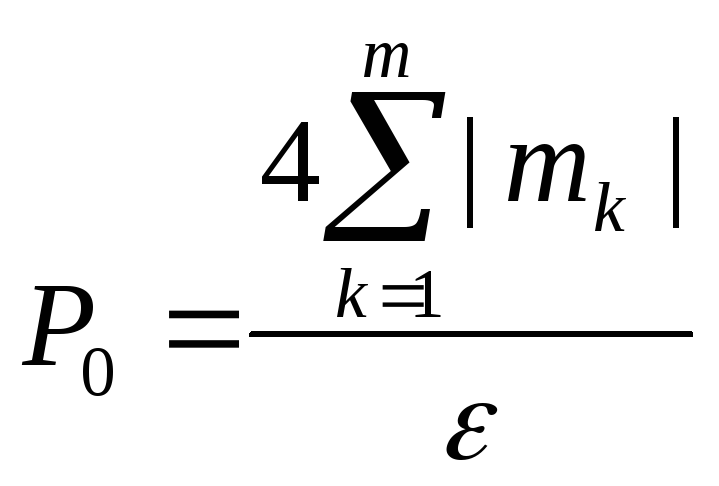 .
Тогда для любого
.
Тогда для любого
![]() из (4.4) получим
из (4.4) получим![]() .
.
Предел (1.4) доказан по определению. Предел (2.4) доказывается аналогично. Лемма доказана.
Следствие 1.4.Пустьf(x) определена на промежутке (a,b] (либо на [a,c)).
Если
![]() для
любого
для
любого![]() f(x)
не ограничена в правой окрестности
точкиа(левой окрестности точкиb)
и несобственный интеграл второго рода
f(x)
не ограничена в правой окрестности
точкиа(левой окрестности точкиb)
и несобственный интеграл второго рода![]() сходится абсолютно, то равенства (1.4) и
(2.4) также выполнены, только слева в этих
равенствах берутся несобственные
интегралы второго рода.
сходится абсолютно, то равенства (1.4) и
(2.4) также выполнены, только слева в этих
равенствах берутся несобственные
интегралы второго рода.
Доказательство
Берем
![]() .
Так как
.
Так как![]() ,
то
,
то![]() такое, что
такое, что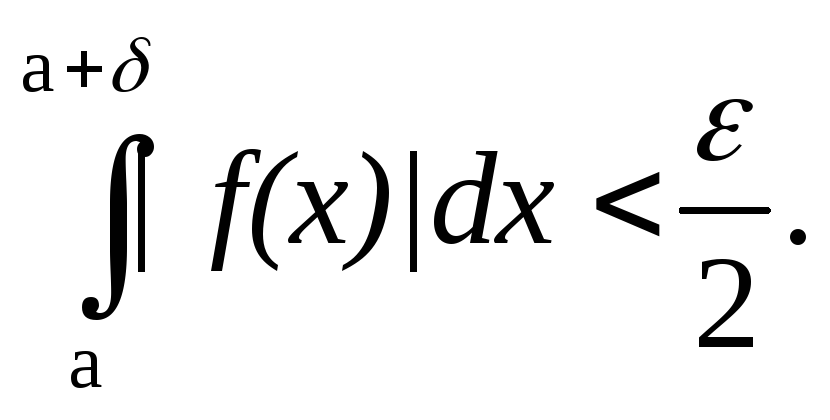 Поскольку по условию
Поскольку по условию![]() то согласно теореме Римана существует
то согласно теореме Римана существует![]() такое,
что для любого
такое,
что для любого
![]() выполнено
выполнено![]() .
Следовательно
.
Следовательно![]() Предел (1.4) доказан. Предел (2.4) доказывается
точно также. Еслиfимеет особенность в точкеb,
то следствие доказывается аналогично.
Следствие доказано.
Предел (1.4) доказан. Предел (2.4) доказывается
точно также. Еслиfимеет особенность в точкеb,
то следствие доказывается аналогично.
Следствие доказано.
