
- •§1. Определение пространства .
- •§2. Ряд Фурье.
- •Ортонормированные системы в евклидовом пространстве.
- •2. Ортонормированные системы в k[] и k[a,b].
- •3. Определение ряда Фурье.
- •4. Замкнутые системы в евклидовых пространствах.
- •§3. Тригонометрический ряд Фурье.
- •1. Замкнутость тригонометрической системы.
- •2. Тригонометрическая система в пространстве интегрируемых функций.
- •3. Ряд Фурье по тригонометрической системе (3.2).
- •4.Тригонометрический ряд Фурье в пространстве .
- •5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.
- •Комплексная форма записи тригонометрического ряда Фурье.
- •§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
- •1. Свойства интегрируемых функций
- •2. Интегральное представление частичных сумм тригонометрического ряда Фурье
- •3. Необходимое и достаточное условие сходимости ряда Фурье в точке
- •4.Достаточные условия поточечной сходимости ряда Фурье.
- •5. Примеры.
§3. Тригонометрический ряд Фурье.
1. Замкнутость тригонометрической системы.
Рассмотрим в пространстве кусочно-непрерывных
функций
![]() ортонормированную систему (3.2). Скалярное
произведение в пространстве
ортонормированную систему (3.2). Скалярное
произведение в пространстве![]() задается формулой (5.1).
задается формулой (5.1).
Определение 1.1.
Тригонометрическим многочленом
называют выражение вида![]() ,
где
,
где![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
…,
,
…,![]() произвольные действительные числа.
произвольные действительные числа.
Доказательство замкнутости тригонометрической системы опирается на следующую теорему Вейерштрасса:
Теорема 1.3.Любую непрерывную на
отрезке![]() функцию
функцию![]() такую, что
такую, что![]() (т.е.
(т.е.![]() )
можно равномерно приблизить
тригонометрическими многочленами, то
есть
)
можно равномерно приблизить
тригонометрическими многочленами, то
есть![]()
![]() такой, что
такой, что![]()
![]() .
.
Теорема 2.3. Тригонометрическая
система (3.2) замкнута в![]() .
.
Доказательство теоремы опирается на следующие вспомогательные утверждения.
Лемма 1.3.Для любой интегрируемой
по Риману на отрезке![]() функции
функции![]() и
и![]() найдется кусочно-постоянная на
найдется кусочно-постоянная на![]() функция
функция![]() принимающая конечное число значений и
такая, что
принимающая конечное число значений и
такая, что

![]() (1.3)
(1.3)
Лемма 2.3.Для любой функции![]() ,
принимающей конечное число значений,
и
,
принимающей конечное число значений,
и![]() найдется функция
найдется функция![]() такая, что
такая, что
 (2.3)
(2.3)
Доказательство леммы 1.3.
Возьмем любую интегрируемую на отрезке
![]() функцию
функцию![]() и
и![]() .
Из интегрируемости вытекает ограниченность.
Пусть
.
Из интегрируемости вытекает ограниченность.
Пусть![]() .
Из критерия интегрируемости следует,
что найдется разбиение отрезка
.
Из критерия интегрируемости следует,
что найдется разбиение отрезка![]() точками
точками![]() ,
,![]() ,
…,
,
…,![]() такое, что
такое, что![]() и
и ,
где
,
где![]() ,
,![]() верхняя и нижняя суммы Дарбу соответственно.
Здесь
верхняя и нижняя суммы Дарбу соответственно.
Здесь![]() ,
,![]() ,
,![]() .
Определим функцию
.
Определим функцию
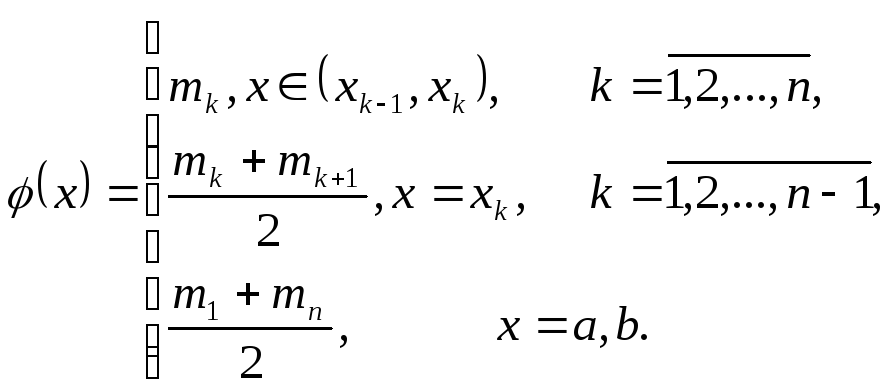
Очевидно, что
![]() и принимает конечное число значений.
Найдем
и принимает конечное число значений.
Найдем
 .
Лемма 1.3 доказана.
.
Лемма 1.3 доказана.
Доказательство леммы 2.3.
Пусть функция
![]() и принимает конечное число значений.
Возьмем
и принимает конечное число значений.
Возьмем![]() .
Пусть
.
Пусть![]() ,
,![]() ,
…,
,
…,![]() все точки разрыва функции
все точки разрыва функции![]() на интервале
на интервале![]() .
Обозначим
.
Обозначим![]() ,
,![]() .
Выберем число
.
Выберем число![]() ,
где
,
где![]() ,
,![]() .
Определим функцию
.
Определим функцию

Здесь коэффициенты
![]() ,
,![]() подобраны так, что прямая
подобраны так, что прямая![]() при
при![]() проходит через точки
проходит через точки![]() ,
а при
,
а при![]() через точки
через точки![]()
Обозначим
![]() .
Оценим
.
Оценим
![]() .
.
Подберем
![]() так, чтобы дополнительно выполнялось
неравенство
так, чтобы дополнительно выполнялось
неравенство![]() Тогда
Тогда![]() Лемма доказана.
Лемма доказана.
Доказательство теоремы 2.3.
Возьмем
![]() и
и![]() .
Функция
.
Функция![]() интегрируема на отрезке
интегрируема на отрезке![]() ,
так как ограничена и имеет конечное
число точек разрыва. Тогда из леммы 1.3
следует, что найдется кусочно-постоянная
функция
,
так как ограничена и имеет конечное
число точек разрыва. Тогда из леммы 1.3
следует, что найдется кусочно-постоянная
функция![]() ,
принимающая конечное число значений и
такая, что
,
принимающая конечное число значений и
такая, что![]() Согласно лемме 2.3 существует функция
Согласно лемме 2.3 существует функция![]() такая, что
такая, что![]() А из теоремы Вейерштрасса вытекает
существование тригонометрического
многочлена
А из теоремы Вейерштрасса вытекает
существование тригонометрического
многочлена![]() такого, что
такого, что![]()
![]() Тогда
Тогда![]() Поэтому
Поэтому![]() Теорема доказана.
Теорема доказана.
Следствие 1.3.Тригонометрическая
система (4.2) замкнута в пространстве![]()
Доказательство.
Возьмем
![]() и
и![]() .
Тогда функция
.
Тогда функция![]() и согласно теореме 2.3 существует
тригонометрический многочлен
и согласно теореме 2.3 существует
тригонометрический многочлен![]() такой, что
такой, что![]() .
.
Поэтому

и, следовательно,
![]() ,
что завершает доказательство, поскольку
тригонометрический многочлен
,
что завершает доказательство, поскольку
тригонометрический многочлен![]() равен линейной комбинацией функций из
системы 4.2.
равен линейной комбинацией функций из
системы 4.2.
2. Тригонометрическая система в пространстве интегрируемых функций.
Обозначим через
![]() множество функций, интегрируемых по
Риману на отрезке
множество функций, интегрируемых по
Риману на отрезке![]() .
Множество
.
Множество![]() - линейное пространство. Это вытекает
из линейных свойств интеграла Римана.
Если попытаться ввести в
- линейное пространство. Это вытекает
из линейных свойств интеграла Римана.
Если попытаться ввести в![]() скалярное произведение по формуле
(5.1), то первая аксиома скалярного
произведения не выполнится. Действительно,
для функции
скалярное произведение по формуле
(5.1), то первая аксиома скалярного
произведения не выполнится. Действительно,
для функции![]()
![]() везде на
везде на![]() ,
кроме быть может, множества меры 0.
Напомним, что числовое множество имеет
меру 0, если
,
кроме быть может, множества меры 0.
Напомним, что числовое множество имеет
меру 0, если![]() существует конечная или счетная система
интервалов, суммарная длина которых
меньше
существует конечная или счетная система
интервалов, суммарная длина которых
меньше![]() ,
а объединение содержит данное множество.
Таким образом,
,
а объединение содержит данное множество.
Таким образом,![]() может не равняться тождественно 0.
может не равняться тождественно 0.
Определение 1.3.Говорят, что
некоторое свойство справедливо почти
всюду на отрезке![]() ,
если оно выполнено для всех точек
,
если оно выполнено для всех точек![]() ,
кроме, быть может, множества меры 0.
,
кроме, быть может, множества меры 0.
Будем говорить, что две функции
![]() и
и![]() эквивалентны и писать
эквивалентны и писать![]() ~
~![]() ,
если они равны почти всюду на отрезке
,
если они равны почти всюду на отрезке![]() .
.
Легко проверить, что это действительно
отношение эквивалентности. Поэтому
множество интегрируемых функций
![]() разбивается на непересекающиеся классы
по отношению эквивалентности.
разбивается на непересекающиеся классы
по отношению эквивалентности.
Обозначим через
![]() множество классов эквивалентных, то
есть равных почти всюду функций из
множество классов эквивалентных, то
есть равных почти всюду функций из![]() .
.
Стандартным образом в
![]() вводится структура линейного пространства.
Каждую функцию из данного класса будем
называть представителем этого класса.
вводится структура линейного пространства.
Каждую функцию из данного класса будем
называть представителем этого класса.
Под суммой двух классов из
![]() будем считать класс, содержащий сумму
двух представителей этих классов.
будем считать класс, содержащий сумму
двух представителей этих классов.
Для
![]() и любого класса
и любого класса![]() определим
определим![]() как класс, содержащий произведение
как класс, содержащий произведение![]() на представитель класса
на представитель класса![]() .
.
Задача 1.3.Проверить, что так
определенные операции сложения и
умножения на число в![]() не зависят от представителей данных
классов.
не зависят от представителей данных
классов.
Нулем в пространстве
![]() является класс, состоящий из функций
равных 0 почти всюду на
является класс, состоящий из функций
равных 0 почти всюду на![]() .
Легко проверить в
.
Легко проверить в![]() выполнение всех аксиом линейного
пространства.
выполнение всех аксиом линейного
пространства.
В дальнейшем, если это не будет вызывать
недоразумений, будем обозначать одними
и теми же буквами
![]() как сами классы из
как сами классы из![]() ,
так и их представителей. А само пространство
,
так и их представителей. А само пространство![]() ,
как и
,
как и![]() ,
будем называть пространством интегрируемых
по Риману функций на отрезке
,
будем называть пространством интегрируемых
по Риману функций на отрезке![]() .
.
Определим в
![]() скалярное произведение по следующему
правилу:
скалярное произведение по следующему
правилу:
![]() положим
положим
![]() (3.3)
(3.3)
где под интегралом стоит произведение
произвольных двух представителей
классов
![]() Из свойств интеграла Римана следует,
что интеграл в формуле (3.3) существует
и одинаков для всех представителей
классов
Из свойств интеграла Римана следует,
что интеграл в формуле (3.3) существует
и одинаков для всех представителей
классов![]() и
и![]() .
Теперь легко проверить выполнение всех
аксиом скалярного произведения. Таким
образом,
.
Теперь легко проверить выполнение всех
аксиом скалярного произведения. Таким
образом,![]() является евклидовым пространством со
скалярным произведением (3.3). Сходимость
по норме, порожденной скалярным
произведением (3.3) (т.е.
является евклидовым пространством со
скалярным произведением (3.3). Сходимость
по норме, порожденной скалярным
произведением (3.3) (т.е.![]() )
называется сходимостью в среднем.
)
называется сходимостью в среднем.
Очевидно, что тригонометрическая система
(3.2) (точнее, система классов функций
эквивалентных функциям из (3.2)) является
ортонормированной системой в
![]() .
.
Теорема 3.3.Тригонометрическая
система (3.2) замкнута в пространстве![]() .
.
Доказательство теоремы 3.3 полностью
повторяет доказательство теоремы 2.3
поскольку лемма 1.3 доказана нами для
функций из
![]() .
Если в доказательстве следствия 1.3
заменить пространство
.
Если в доказательстве следствия 1.3
заменить пространство![]() ,
на пространство
,
на пространство![]() ,
то получим доказательство следующего
следствия из теоремы 3.3.
,
то получим доказательство следующего
следствия из теоремы 3.3.
Следствие 2.3.Тригонометрическая
система (4.2) замкнута в пространстве![]() .
.
Из замкнутости тригонометрической
системы (4.2) и теоремы 4.2 следует, что для
функции
![]() либо из пространства
либо из пространства![]() ,
либо из
,
либо из![]() ряд Фурье сходится к
ряд Фурье сходится к![]() в среднем и имеет место равенство
Парсеваля.
в среднем и имеет место равенство
Парсеваля.
