
Совершенное множество является замкнутым и не имеет изолированных
точек.
Лемма. Для того чтобы точка x являлась изолированной точкой мно-
жества F необходимо и достаточно, чтобы она была общим кон-
цом двух соседних смежных интервалов.
Доказательство:
() Пусть x0 изолированная точка множества F. Тогда по определению V(x0,), в которой кроме x0 нет ни одной точки x. Рассмотрим (x0, x0), не содержащий ни одной точки из F он принадлежит некоторому смежному интервалу ( , ), = x0. Аналогично интервал (x0, x0+) не содержит точек из F содержится в смежном интервале (x0,). Итак, x0 является правым концом некоторого смежного интервала ( , x0) и левым концом интервала (x0,).
() Пусть x0конец двух соседних смежных интервалов, x0F.
Обозначим =min (x0-, x0-). Рассмотрим V(x0,). В ней нет ни
одной точки множества F, кроме точки x0. По определению x0изолиро-
ванная точка множества F.
Из теоремы 6, теоремы 7 и леммы следует утверждение о строении совер-
шенных множеств.
Теорема 8 (О строении совершенного ограниченного множества).
Для того чтобы ограниченное множество было совершенным
необходимо и достаточно, чтобы оно являлось либо отрезком,
либо получалось из некоторого отрезка удалением конечного
или счетного множества интервалов, не имеющих ни общих
концов друг с другом, ни с отрезком.
Теорема 8 (О строении совершенного множества).
Для того чтобы множество было совершенным необходимо и
достаточно, чтобы оно являлось или прямой R, или получа-
лось из R удалением конечного или счетного множества не-
пересекающихся интервалов, не имеющих общих концов
друг с другом.
Пример. Канторово множество.
Оно является ограниченным, замкнутым, совершенным. (Множество по-
лучено из [0,1] удалением из него счетного множества попарно не пе-
ресекающихся интервалов, не имеющих общих точек ни друг с другом,
ни с концами [0,1]. Значит, по теореме 8 множество является совершен-
ным).
Измеримые множества, измеримые функции.
Интеграл Лебега.
Опр.1. Мерой интервала (a,b),a<b называется его длина, т.е. число m=m(a , b)=b-a.
Очевидно, что m(a , b)>0.
Всякое открытое множество является объединением конечного или
счетного множества попарно не пересекающихся интервалов, которые
называются составляющими интервалами открытого множества.
Пусть
G
открытое множество. Тогда G=![]() ,
где
,
где
![]() .
.
Т.к. G ограничено, то оно содержится в некотором интервале (a , b), мера
которого определена m(a , b)=b-a.
Очевидно, что k k (a , b).
Итак, интервалы k не пересекаются попарно и содержатся в интервале
(a , b).
Рассмотрим два случая:
1.G
конечное объединение интервалов
k
, т.е. G=![]() .
.
Мера интервала k это 0m( k )<+.
0![]() <+
<+
![]() положительное
число, выражающее собой сумму мер
непересе-
положительное
число, выражающее собой сумму мер
непересе-
кающихся интервалов, входящих в состав множества G.
2.Пусть
Gсчетное
объединение интервалов
k
, т.е. G=![]()
Рассмотрим
ряд
![]() (1) положительный
числовой ряд.
(1) положительный
числовой ряд.
S
n
=![]()
n-ая
частичная сумма ряда.
n-ая
частичная сумма ряда.
Если m k0, то последовательность {S n} будет не убывающая, возрас-
тающая и ограничена сверху (см. п.1.) lim S n=S по определению ряд (1) сходится и его сумма есть неотрицательное число, т.е.
0![]()
(Ряд сходится, когда существует предел
последовательности его частичных
сумм).
(Ряд сходится, когда существует предел
последовательности его частичных
сумм).
Итак, если Gоткрытое ограниченное множество, то сумма мер его составляющих интервалов не отрицательное число, не большее, чем b-a.
Опр.2. Мерой ограниченного открытого множества G называется сумма
мер его
составляющих интервалов, т.е. если
G=![]() ,
то
,
то
mG=![]() .
Ясно, что 0mG.
.
Ясно, что 0mG.
Свойства меры открытого ограниченного множества.
Теорема 1. Если ограниченное открытое множество G является объедине-
нием конечного числа или счетного множества попарно непе- ресекающихся открытых множеств G k, то мера множества G
равна сумме
мер множеств, т.е. mG=![]() .
.
Доказательство: возьмем G kоткрыто может быть представлено в
виде
G
k=![]() ,
где
,
где
![]() =,
ij.
=,
ij.
G=![]() .(2)
.(2)
В правой части (2) не более чем счетное число интервалов. Т.к. G k не
пересекаются попарно, то и интервалы в (2) попарно не пересекаются.
Следовательно, они являются составляющими интервалами для множест-
ва
G
. По определению 2 mG=![]() .
.
Теорема 2. Пусть G 1, G 2 открытые ограниченные множества, т.ч.G 1G 2.
Тогда m G 1 mG 2.
Доказательство:![]() .
.
Возьмем любой составляющий интервал k(1) множества G 1.
Для любого k(1) существует составляющий интервал m(2): k(1) m(2)
m k(1)m m(2).
Просуммируем
по k
и получим неравенство:
![]() .
.
mG
1![]()
![]() mG
2.
mG
2.
Мера ограниченного замкнутого множества.
Опр.1. Мерой пустого множества называется число ноль.
Пусть F ограниченное замкнутое множество. Тогда существует отрезок
![]() =[a
, b]
, содержащий множество F.
Рассмотрим множество C∆F=
=[a
, b]
, содержащий множество F.
Рассмотрим множество C∆F=![]() \F.
\F.
C∆Fоткрытое ограниченное множество (показано ранее) существует мера этого множества. Т.к. C∆F(a , b), то 0m(C∆F)<b-a
0(b-a)-m(C∆F)<+.
Опр.2. Мерой ограниченного замкнутого множества F называется число,
обозначаемое mF и определяемое по формуле: mF=(b-a)-m(C∆F),
где
![]()
наименьший отрезок, содержащий
множество F.
наименьший отрезок, содержащий
множество F.
Ранее было показано, что mFнеотрицательное число.
Свойства меры ограниченного замкнутого множества.
Теорема 3. m[a , b]=b-a.
Доказательство:
в данном
случае
![]() =[a
, b],
C∆[a
, b]=.
=[a
, b],
C∆[a
, b]=.
m[a, b]=(b-a)-m(C∆[a , b])=b-a.
Теорема 4. Пусть [a , b], [c , d] непересекающиеся отрезки. Тогда мера
их объединения равна сумме мер отрезков, т.е.
m([a , b] [c , d])=m[a , b]+m[c , d].
Доказательство:
![]() =[a
, d]
C∆([a
, b][c
, d])=(b , c)
m([a , b]
[c , d])=
=[a
, d]
C∆([a
, b][c
, d])=(b , c)
m([a , b]
[c , d])=
m![]() -m(C∆([a
, b][c,
d])=m[a, d]-m (b, c)=d-a-(c-b)=d-a-c + b=(b-a)+(d-c)=
-m(C∆([a
, b][c,
d])=m[a, d]-m (b, c)=d-a-(c-b)=d-a-c + b=(b-a)+(d-c)=
m[a, b]+m[c, d].
Теорема 5. Пусть F ограниченное замкнутое множество, содержащееся
в интервале G=(c , d). Тогда mF=mG-m(C GF).
Доказательство: Пусть =[a , b]наименьший отрезок, содержащий мно-
жество F. Тогда по определению mF=(b-a)-m(C∆F)=((d-b)+(b-a)+(a-c))-
-(m(C∆F)+(d-b)+(a-c))=(d-c)- m(C GF)=mG- m(C GF).
Теорема 6. Если F1,F2 ограниченные замкнутые множества и F1 F2 ,то
m F1m F2.
Доказательство: Пусть G открытое множество, т.ч. F2G F1G.
(это, возможно, сделать, т.к. F2 ограничено). Рассмотрим множества
C GF1 и C GF2. Имеем C GF1 C GF2открытые множества. Действительно,
пусть x C GF2 xG, xF2, но F1F2xG,xF1x C GF1. По т.2.
m (C GF1)m(C GF2)- m (C GF1)- m (C GF2)mG- m (C GF1)- m (C GF2)+mG
mF1m F2.
Лемма Гейне-Бореля.
Пусть F, Mметрическое пространство.
Лемма. Пусть F замкнутое ограниченное множество,{( k, k)}k=1систе-
ма интервалов, покрывающих множество
F,
т.е. F
![]() .
.
Тогда существует конечное число интервалов ( k1, k1) ,…,( kn, kn)
покрывающих множество F,
т.е. т.ч.
F
![]() (
ki,
ki),
i=1,…,n.
(
ki,
ki),
i=1,…,n.
Опр.1. Fкомпактно F замкнуто и ограничено.
Опр.2. F компактно, если из любого бесконечного множества покрытий
множества F можно выделить конечное число подпокрытий мно-
жества F.
Доказательство леммы: Пусть F замкнутое ограниченное множество,
F[a, b]. [a , b]наименьший отрезок, содержащий множество F. Докажем
от противного. Предположим, что из бесконечной системы интервалов
нельзя выбрать конечную систему, покрывающую F.
Делим
отрезок [a
, b]
на два равных отрезка [a
,![]() ],
[
],
[![]() ,b].
Хотя бы один из них нельзя покрыть
конечным числом интервалов. Обозначим
его u1.
Далее u1
делим на
два равных отрезка, и за u2
обоз-
,b].
Хотя бы один из них нельзя покрыть
конечным числом интервалов. Обозначим
его u1.
Далее u1
делим на
два равных отрезка, и за u2
обоз-
начаем тот из них, который нельзя покрыть конечным числом интерва-
лов. Процесс продолжим до бесконечности. Получим последовательность
отрезков u1 u2 u3… u n…
Для последовательности {u n} имеем:
u n nN нельзя покрыть конечным числом интервалов по построению и
предположению в u n содержится бесконечное число точек множества F.
u nпоследовательность вложенных отрезков, u n=
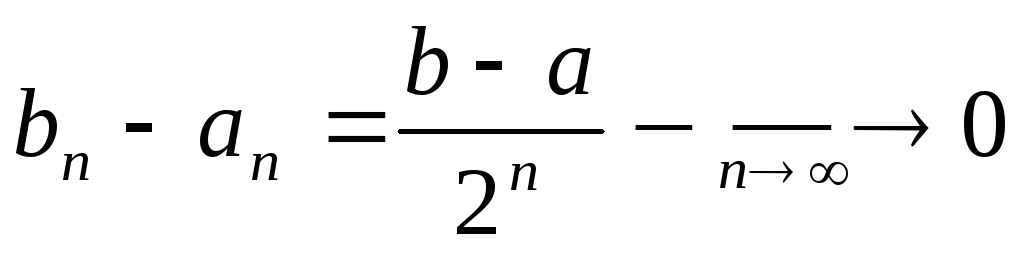 .
.
Тогда
по принципу вложенных отрезков
![]() .
.
Покажем, что x0F.
Из п.1. следует, что (x n): x n u nF, a n x nb n nN.
lim x n=x0 по теореме о пределе промежуточной последовательности.
x0 предельная точка множества F, но F замкнутоx 0Fk0: x0(k0,k0).
b n-a n0, n N: n>N: u n(k0,k0).
Итак, все отрезки последовательности u n, начиная с номера N+1 содер-
жатся в фиксированном интервале (k0,k0), т.е. покрываются одним ин-
тервалом из данной системы. Противоречие с предположением, следова-
тельно предположение не верно.
Внешняя мера.
Пусть ограниченное множество, (a , b). Возьмем всевозможные от-
крытые множества G, покрывающие множество . Мера множества G
определена в предыдущих пунктах: 0mG<+.
Опр.1. Пусть множество всевозможных множеств, которые покрыва-
ют множество . Внешней мерой множества называется число, обозначаемое m*E и определяемое по формуле:
m*E=![]() {mG}.
{mG}.
Свойства внешней меры множества.
Свойство 1. m*E0
Доказательство:
m*E
=
![]() {mG}.
{mG}.
0mG<+ GA(E) m*E = inf{mG}0.
Свойство 2. E1E2 m*E1 m*E2.
Доказательство: Рассмотрим A(E1) и A(E2). A(E1) A(E2).
Если множество расширяется, то его inf может только уменьшится.
GA(E2)
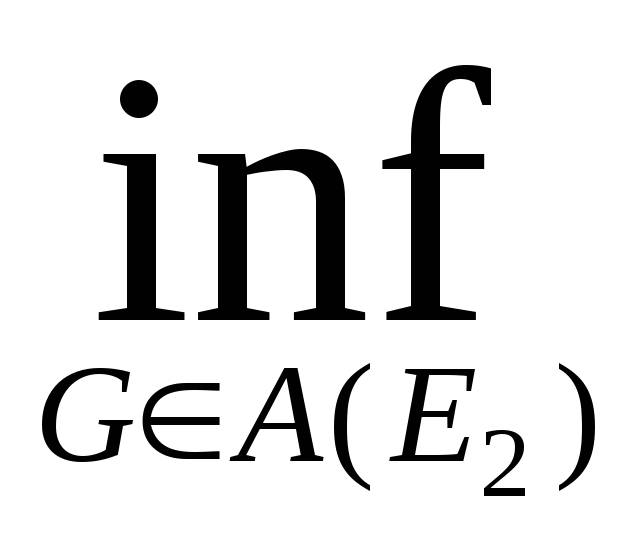 {mG}
{mG}
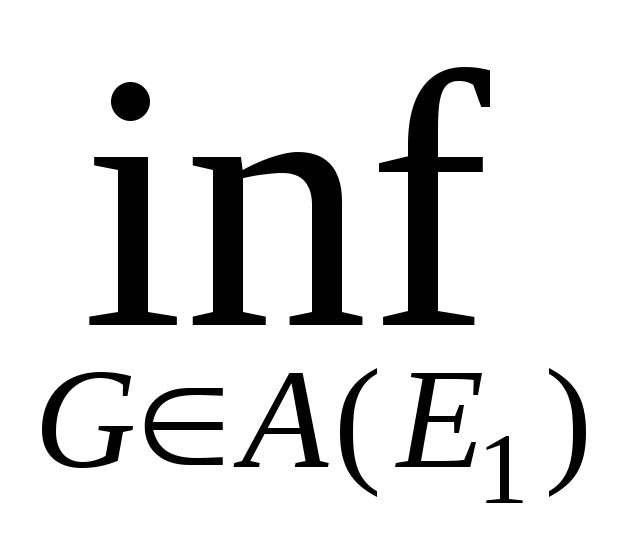 {mG},GA(E1)
m*E1
m*E2.
{mG},GA(E1)
m*E1
m*E2.
Лемма
1. Пусть {O
k}k=1
система открытых множеств. O=![]() .
.
Тогда m(O)=![]() ,
если последний ряд сходится.
,
если последний ряд сходится.
Доказательство:
т.к. Oоткрытое
множество, то O=![]() (A
k,B
k),
(A
k,B
k)
(A
k,B
k),
(A
k,B
k)
непересекающиеся попарно интервалы.
m(O)=![]() (Bk-A
k)=
(Bk-A
k)=![]() .
.
O
n=![]() (a
nm
, b
nm)объединение
попарно непересекающихся интервалов
n.
(a
nm
, b
nm)объединение
попарно непересекающихся интервалов
n.
m(O
n)=![]() (bnm-
a nm).
(bnm-
a nm).
Возьмем интервал (A k,B k).
O=![]() (a
nm ,
b
nm).
(a
nm ,
b
nm).
Выберем
>0:
k=![]() .Получим
.Получим
[A
k
+
k
,
B k-
k](A
k,
B k)O=![]() (a
nm,
b
nm).
(a
nm,
b
nm).
Система интервалов (a nm, b nm)система, покрывающая [A k + k , B k- k].
По лемме Гейне-Бореля из нее можно выбрать конечную систему интер-
валов, покрывающих данный отрезок: [A k + k , B k- k] (k)(a nm, b nm).
Тогда B k-A k-2 k(k) (b nm-anm) B k-A k(k) (b nm-anm)+ 2 k.
Просуммируем
по k:
![]() .
.
m(O)
![]() (k)
(b nm-anm)+
.
(1)
(k)
(b nm-anm)+
.
(1)
![]() .
.
Из
(1) m(O)
![]() при0.
при0.
Свойство
3. Пусть E=![]() m*E
m*E
![]() m*E
n.
m*E
n.
Доказательство: возьмем nN и рассмотрим множество E n. По опре-
делению
m*E
n=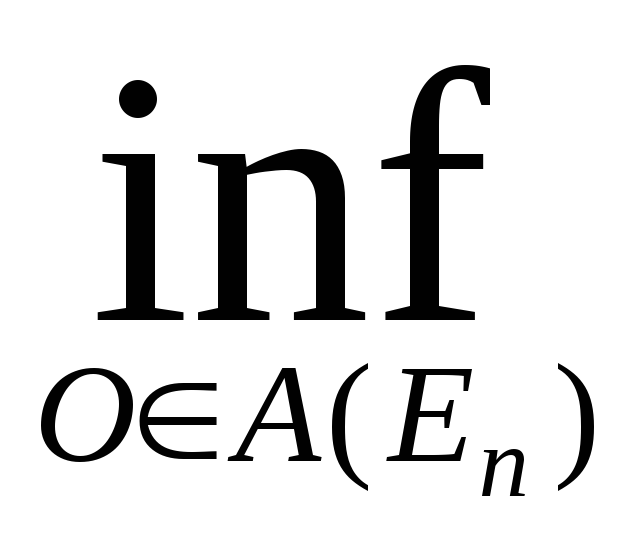 {mO}
O
n:
m(O
n)
m*E
n+
{mO}
O
n:
m(O
n)
m*E
n+![]() .
.
Просуммируем по n все такие неравенства:
![]() .
.
EO,
O=![]() On
(E nO
n
nN,
On
(E nO
n
nN,
![]() ).
).
По
свойству 2 m*Em(O)![]() m*(O
n)
m*(O
n)
![]() m*E
n+.
m*E
n+.
Переходим
к пределу при 0
и получаем: m*E
![]() m*E
n.
m*E
n.
Внутренняя мера.
Пусть
![]() =(0,1),
=(0,1),![]() .
РассмотримC∆E=
.
РассмотримC∆E=![]() \E
\E![]() .
Величинаm*(C∆E)
определена в предыдущем пункте.
.
Величинаm*(C∆E)
определена в предыдущем пункте.
Опр. Внутренней мерой множества E называется число, обозначаемое
m*E и определяемое по формуле: m*E=1- m* (C∆E).
Свойства внутренней меры.
1.а) m *E m*E
Доказательство:
рассмотрим отрезок [
, 1-],
E(0,1)=![]() .C∆E=
.C∆E=![]() \E
(0,1),
\E
(0,1),
т.е. E C∆E=(0,1).
Пусть G1 покрывает E, G1открытое множество, G2 покрывает C∆E,
G2 открытое множество. Для выбранного отрезка [ , 1-], G1A(E),
G2A(C∆E).
Т.к. G1
и G2
открыты, то G1=![]() (
k,
k),
G2=
(
k,
k),
G2=![]() (
m,
m),
где
(
m,
m),
где
( i, i)( j, j)=, i j, ( s, s)( p, p)=, sp.
Рассмотрим G=G1G2открытое множество. Очевидно, что G покрывает
отрезок [ , 1-] (ограниченное замкнутое множество)по лемме Гейне-
Бореля из нее можно выделить конечную систему интервалов, покрыва-
ющих отрезок [ , 1-]. Выпишем ее: ( 1, 1),…, ( n, n) (1)
( 1, 1),…, ( m, m) (2)
Интервалы систем (1) и (2) между собой могут пересекаться.
1--![]()
![]() 1-2
(3)
1-2
(3)
Т.к. G1 и G2 любые открытые множества из A(E) и A(C∆E), то по оп-
ределению нижней грани можно подобрать точку, чтобы выполнялись
следующие условия:
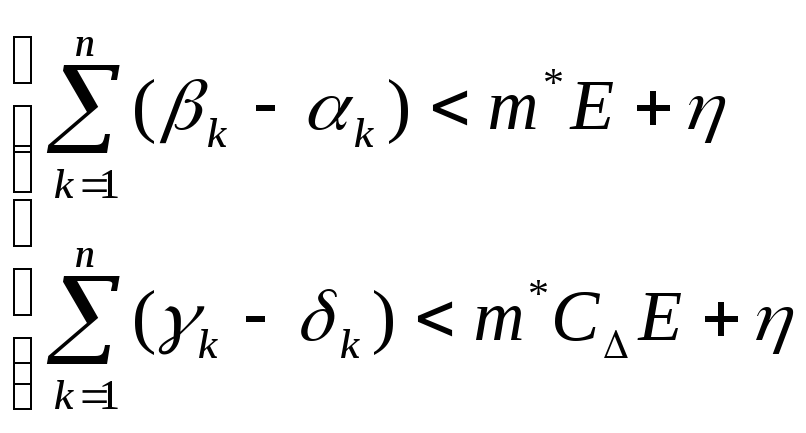 (4)
(4)
Тогда из (3) и (4) m*E+ m*C∆E+21-2.
Переходя в последнем неравенстве к пределу при ,0, получим:
m*E1- m*C∆E m*E m*E.
б) m*E0.
Доказательство:
(0,1)=![]() . 1-
m*C∆E0
m*C∆E1.
. 1-
m*C∆E0
m*C∆E1.
Возьмем (0,1). Возьмем любое открытое множество G, содержащее E,
т.ч. mG<1+.
EG m*E m*G.
m*G=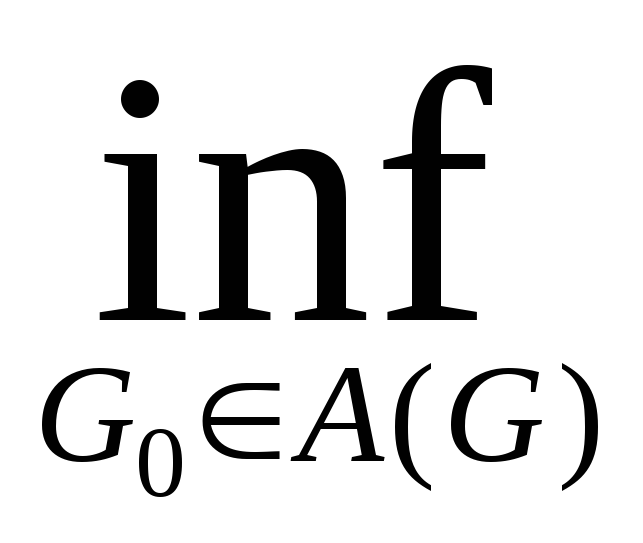 {mG0}=mG
m*G=mG
{mG0}=mG
m*G=mG
m*E<1+.
Переходя к пределу при 0, получим: m*E1т.к. C∆E(0,1), то m*C∆E1.
Лемма 1. Пусть O и O ограниченные открытые множества, покрываю-
щие интервал (0,1). Тогда m(O O)m(O)+m(O)-1.()
Доказательство: По условию O
и O
ограниченные открытые мно- жестваO=![]() (
k,
k),
(
i,
i)(
j,
j)=,
i
j.
(
k,
k),
(
i,
i)(
j,
j)=,
i
j.
O=![]() (
m,
m),
(
s,
s)(
p,
p)=,
sp.
(
m,
m),
(
s,
s)(
p,
p)=,
sp.
Возьмем и рассмотрим отрезок [,1-]. Т.к. OO(0,1) [,1-] , то по лемме Гейне-Бореля из этих интервалов можно выделить конечное число интервалов, покрывающих [,1-]: ( k1, k1),…,( kn, kn)
( m1, m1),…, ( mp, mp).
[,
1-]{![]() (
kj,
kj)}{
(
kj,
kj)}{![]() (
mj,
mj)}.
Обозначим
через N1=
(
mj,
mj)}.
Обозначим
через N1=![]() kj,
kj,
N2=![]() mj
,
mj
,
N=max{N1, N2}.
Т.к.
O и
Oограничены,
то сходятся ряды
![]() (
k-
k)мера
,
(
k-
k)мера
,
![]() (
m-
m)мера
.
Для
N0N
(
m-
m)мера
.
Для
N0N
![]() ;
;
![]() {т.к.
Q
n
абсолютно
сходится
lim
R
n=0}
{т.к.
Q
n
абсолютно
сходится
lim
R
n=0}
Обозначим
через =max
{N,N0},
Q=![]() (
k,
k),
Q=
(
k,
k),
Q=![]() (
k,
k),
(
k,
k),
R=![]() (
k,
k),
R=
(
k,
k),
R=![]() (
k,
k).
(
k,
k).
O=QR, O= QR, RQ будет покрывать [,1-].
Рассмотрим QQ)(RR)=X. Пусть xxO,xO
а) xQ,xQxQQxX
б) xQ, xQxR или x RxRRxX
m()m(QQRR)m(QQ)+m(R)+m(R)<m(QQ)+![]() =
=
=m(QQ)+ (1)
1--m(Q)+m(Q)-m(QQ)m(QQ)m(Q)+2-1 (2)
Из (1), (2), (3) m()-m(O)+m(O)+2-1, т.е. m()m(O)+m(O)+3-1. Переходим к пределу при 0, получим (*).
Лемма
2. Пусть {E
k}k=1![]()
система попарно непересекающихся
система попарно непересекающихся
множеств, т.е.
E
k
E
m=,
km.
Пусть E=![]() E
k
. Тогда
E
k
. Тогда
m*E![]() m*E
k.
(**)
m*E
k.
(**)
Доказательство:
Пусть k=2. Даны множества E1, E2: E1E2=. Докажем:
m*E= m*(E1E2) m*E1+ m*E2. (4)
Докажем вспомогательные утверждения:
1)Если
E1,
E2
(0,1)=
![]() ,E1E2=Y=
C∆E1
C∆E2(0,1).
,E1E2=Y=
C∆E1
C∆E2(0,1).
Пусть x(0,1)а) xE1xE2x C∆E2xY.
б) xE1x C∆E1xY.
2)C∆E1 C∆E2 = C∆E=C∆(E1E2)
Пусть x C∆E1 C∆E2x C∆Ei, i=1,2xE1,xE2xE1E2x C∆(E1E2)
Пусть x C∆(E1E2) xE1E2 xE1,xE2 x C∆E1 C∆E2
По определению внешней меры (4) перепишем в виде:
1-m*(C∆(E1E2))1-m*(C∆E1)+1- m*(C∆E2)
m*(C∆E1)+
m*(C∆E2)=
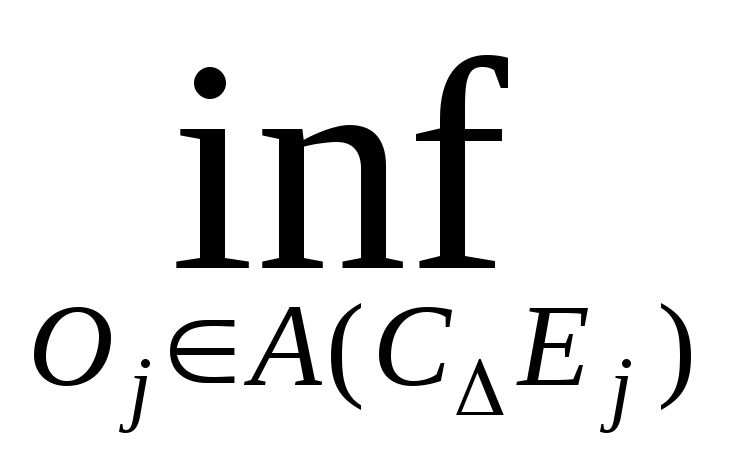 {m(Oj)},
j=1,2.
Ojоткрытое
множество, покрывающее множество C∆Ej.
{m(Oj)},
j=1,2.
Ojоткрытое
множество, покрывающее множество C∆Ej.
>0 O1, O2: O1 C∆E1, O2 C∆E2
а) m(O1)< m*(C∆E1)+, m(O2)< m*(C∆E2)+
б) C∆E1 C∆E2O1O2
в) C∆E1C∆ E2) O1O2
O1O2(0,1) по лемме 1 m (O1O2)m (O1) + m (O2)-1
m*(C∆(E1E2))=m*(C∆E1 C∆E2)m*(O1O2)=m (O1O2) m (O1) + m (O2)-1<
< m*(C∆E1)+ m*(C∆E2)+2-1.
Перейдем к пределу при 0:
m*(C∆(E1E2))+1 m*(C∆E1)+ m*(C∆E2)
k. Пусть S n=
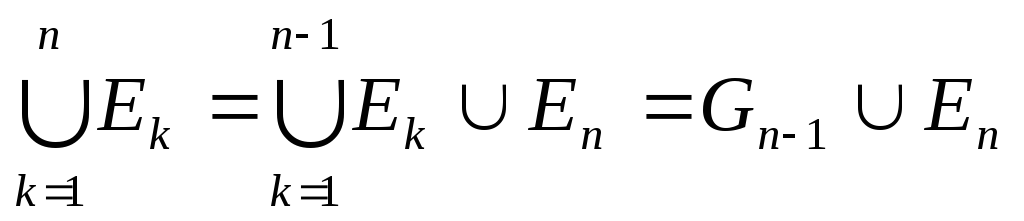 .
.
По 1. m*S nm G n-1+m*E n, S nE. Если E1E2, то m*E1 m*E2
Т.к. S nE C∆S n C∆E m*(C∆S n) m*(C∆E), 1- m*(C∆S n)1- m*(C∆E)
m*S n m*E, m*E m*G n-1+ m*E n
Продолжим
этот процесс: G
n-1=![]() .
По 1.
.
По 1.
m*E
![]() m*E
k.
Перейдем к пределу при n,
получим (**).
m*E
k.
Перейдем к пределу при n,
получим (**).
Измеримые множества. Мера Лебега.
Опр. Пусть E задано на ∆=(0,1). Множество E измеримо по Лебегу, если
m*E=m*E.
Это общее значение обозначается mE и называется мерой множества E.
Свойства:
3.Если измеримо, то C∆E также измеримо.
Доказательство: измеримо m*E=m*E=mE.
Докажем, что C∆E измеримо, т.е. что m* C∆E=m* C∆E.
m* C∆E=1- m*E=1-mE
m* C∆E=1- m*E=1-mE
m* C∆E=m* C∆E.
Лемма 3. Пусть G=(), EG. Множество E измеримо
m*E+ m*(CGE)= -. (1)
Доказательство:
() Пусть E измеримо. Докажем (1). m*E=m*E=mE.
m*E=(-)- m*(CGE) m*(CGE)= (-)-m*E=(-)- mE
m*E+ m*(CGE)= mE+(-)-mE=-.
() Из (1) m*E=(-)- m*(CGE).
По определению m*E=(-)- m*(CGE).
Т.о. m*E=m*E=mEизмеримо.
Основные теоремы об измеримых множествах.
Теорема 1. Пусть E1,E2,…E n,…измеримые множества. Тогда
а)
E=![]() E
k
измеримо,
mE
E
k
измеримо,
mE
![]() mEk.
mEk.
б)
E k
E m=,km.
Тогда
mE=![]() mEk.
mEk.
Доказательство теоремы 1б):
Докажем, что измеримо, т.е. что m*E=m*E.
Т.к.
E
k
E
m=,km,
то по л.2. m*E![]() m*E
k,
но все Ek
измеримы
m*E
k,
но все Ek
измеримы
m*E
![]() mEk
mEk
Из
свойства 3 внешней меры
m*E
![]() m
*E
k
=
m
*E
k
=![]() mE
k,
т.е.
mE
k,
т.е.
![]() mE
k
m*E
m*E
mE
k
m*E
m*E
![]() mEk
m*E=m*E=
mEk
m*E=m*E=![]() mEk.
mEk.
Доказательство теоремы 2 а):
1.Пусть F=()(0,1) измеримое множество. Eпроизвольное измеримое
множество.
Докажем, что EF измеримое множество.
E1=E(), E2=E\E1, E1E2=, E1E2=E.
Пусть открытое множество, содержащее множество , т.е. EO.
O1=O(), O2=O\O1, O1O2=, O1O2=O.
По т.1б) m(O)=m(O1)+m(O2) (1)
Докажем, что m*E=m*E1+m*E2 (2)
E m*E m*O
По определению inf: m*EmO-.
Покажем, что E1O1: xE1xE, x() xO, x() xO1.
Покажем, что E2O2: xE2xE, xE1 xE, x() xO, x O1
xO2.
E1O1 m*E1 m*O1
E2O2 m*E2 m*O2
Складывая два последних неравенства, получим:
m*E1+ m*E2m(O1)+m(O2)=m(O)
m*E m*E1+ m*E2-
E=E1E2 m*E m*E1+ m*E2
m*E1+ m*E2- m*E m*E1+ m*E2
Переходя в последнем неравенстве к пределу при , получим равенство (2) m*E=m*E1+m*E2
Пусть
C∆E=![]() \E(0,1).
\E(0,1).
Аналогично доказывается равенство:
m* C∆E= m*e1+ m*e2, где e1= C∆E(), e2= C∆E\e1.
Т.к. E измеримо, то m*E=mE, m* C∆E= m C∆E.
Складывая два последних равенства, получим:
m*E+ m* C∆E=mE+ m C∆E=1 (по л.1.).
Докажем, что e1=C FE1, т.е. докажем, что C∆E()= C FE1
1.Пусть
x
C∆E()
x
C∆E,
x()
x![]() ,
xE,
x()
xE1,xF
,
xE,
x()
xE1,xF
x C FE1
2.Пусть
x
C
FE1
xF,
xE1
x=![]() ,
xE,
x()
x
C∆E,
x()
,
xE,
x()
x
C∆E,
x()
x C∆E()
E1 C FE1=(), E1e1=()- m*E1+ m*e1 (4)
Складывая (2) и (3), получим:
mE + m(C∆E)= m*E1+ m*E2+ m*e1+ m*e2=1 m*E1+ m*e1=1- m*E2- m*e2=.
E2e2![]() \F.
Докажем это.
\F.
Докажем это.
x![]() \F
x
\F
x![]() ,
xF.
,
xF.
Возможны два случая:
а) xExE1xE2x E2e2
б) xEx C∆E, xe1x2 x E2e2
Из а) и б) следует, что x E2e2
m
(![]() \F)
m*E2+
m*e21-()
m*E2+
m*e21-
m*E2-
m*e2
\F)
m*E2+
m*e21-()
m*E2+
m*e21-
m*E2-
m*e2
Тогда m*E1+ m*e1 (5)
Из (4) и (5) m*E1+ m*e1= m*E1+ m* C FE1=E1измеримо.
2.Пусть Fпроизвольное открытое множество,
Eпроизвольное измеримое множество, E(0,1), F(0,1).
Докажем, что EF измеримо.
F=![]() Fk,
F iF
j=,
ij.
Fk,
F iF
j=,
ij.
EF=E(![]() Fk)
==
Fk)
==![]() (EF
k)
(EF
k)
EF kизмеримо (по 1.), попарно не пересекаются EF измеримо по т.1б).
(EF
i)(EF
j)=,
ij,
m(EF)=![]() m(EF
k).
m(EF
k).
3.Пусть Fпроизвольное измеримое множество. Т.к. Fизмеримо, то C∆F
измеримо.
Пусть O, Oоткрытые множества, т.ч.:
FO: m(O)m*(F)=m(F)m(O)-
C∆FO: m(O)m*( C∆F)m(O)-.
Чтобы показать, что EF измеримо, покажем, что
m*(EF)+m*( C∆(EF))=1 (8)
EOEFm*(EF) m*(EO)
C∆(EF) C∆F(F C∆E)=(C∆FF)(C∆F C∆E)
Проверим последнее включение:
1)xC∆(EF)
x![]() и (xE
или xF)
и (xE
или xF)
x
 и xE
xC∆E
x
и xE
xC∆E
x и x
C∆F
C∆E
и x
C∆F
C∆E
б) x
E1и
xF
xC∆F
x![]() и x
C∆F
C∆E
и x
C∆F
C∆E
m*(C∆(EF))m*(C∆F)+m*(FC∆E) m*(C∆F)+m*(OC∆E), т.к. FC∆EOC∆E
m*(EF)+m*( C∆(EF)) m*(EO)+ m*(C∆F)+m*(OC∆E)m(O)+ m*(C∆F)=
m(O)+ m(C∆F)m(O)+m(O)m(F)+m(C∆F)+2.
Т.к. Fизмеримо, то m(F)+m(C∆F)=1 по л.3.
m*(EF)+m*( C∆(EF))1+2.
Переходя к пределу при , получим, что m*(EF)+m*(C∆(EF))1 (6)
![]() =(EF)(C∆(EF))m(
=(EF)(C∆(EF))m(![]() )=1
m*(EF)+m*(C∆(EF))
(7)
)=1
m*(EF)+m*(C∆(EF))
(7)
Из (6) и (7)(8).
По лемме 3 множество EF измеримо.
Следствие из т.2а). Пусть E1, E2 измеримые множества, т.ч. E2 E1.
Тогда множество E=E1\E2измеримо и его мера
mE=m E1-m E2.
Доказательство: докажем, что измеримо. Не ограничивая общности
можем
считать, что E2![]() =(0,1),
C∆E2
=(0,1),
C∆E2![]() .
.
Покажем, что E=E1 C∆E2.
xE1\E2xE1, xE2xE1, x
 ,
xE2
xE1,
xC∆E2x
E1
C∆E2
,
xE2
xE1,
xC∆E2x
E1
C∆E2xE1 C∆E2 xE1, xC∆E2 xE1, x
 ,
xE2
xE1\E2xE
,
xE2
xE1\E2xE
Из 1.-2. следует, что равенство верно.
Т.к. E2 измеримо, то C∆E2 измеримо E1 C∆E2 измеримо по т.2а), т.е. E измеримо.
Докажем, что mE=m E1-m E2.
E1=EE2, EE2=.
По т.1б) mE1=mE+mE2 mE=m E1-m E2.
Доказательство теоремы 1 а):
E=![]() Ek,
E k
Ek,
E k![]() .
.
Пусть E1, E2 C∆E1=E2
E3=E3 C∆(E1E2)
E4=E4 C∆(E1E2 E3)
…………………………
E k=E k C∆(E1E2… E k-1)
Докажем:
а) E k E m=, km
б)
E=![]() EkE1=A
EkE1=A
а) Пусть m>k. E k=E k C∆(E1E2… E k-1)
E m=E m C∆(E1E2… E m-1)
x0E m x0E m, x0 C∆(E1E2… E m-1)x0 E1E2… E m-1
x0 E k E k E m=, km
б) A=E. Докажем, что AE.
xAx![]() EkE1
EkE1
1.xE1xE
2.x![]() Ekk02:
xE
k0=Ek0
C∆(E1E2…
E k0-1)
xE
k0
xE
Ekk02:
xE
k0=Ek0
C∆(E1E2…
E k0-1)
xE
k0
xE
Докажем, что EA.
xEk0: xE k0 E k0=Ek0 C∆(E1E2… E k0-1):
1.xC∆(E1E2… E k0-1) xE k0 xA
2.x C∆(E1E2… E k0-1)x E1E2… E k0-1A xA.
Докажем, что E k измеримо k.
По условию E k измеримопо свойству 2 C∆E k измеримо.
По т.2а) E2 измеримо.
Предположим, что E2, E3, …, E k-1 измеримы.
Докажем, что E k измеримо.
E k=E k C∆(E1E2… E k-1)
По т.1б) E1E2… E k-1 измеримы C∆(E1E2… E k-1) измеримо.
По т.2а) E k измеримо.
Из а), б) и с учетом измеримости E k по т1б)измеримо.
Докажем,
что mE![]() mE
k.
mE
k.
mE=m*E
![]() m*E
k=
m*E
k=
![]() mEk.
mEk.
Доказательство теоремы 2 б):
E=![]() Ek,
E k(0,1),
kN,
C∆E
k(0,1).
A= C∆E=
C∆(
Ek,
E k(0,1),
kN,
C∆E
k(0,1).
A= C∆E=
C∆(![]() Ek).
Ek).
Покажем,
что A=
C∆(![]() E
k)
=
E
k)
=
![]() (C∆E
k).
(C∆E
k).
1)
xA
x![]() ,
x
,
x![]() Ek
x
Ek
x![]() ,
xE
k0x
C∆E
k0x
,
xE
k0x
C∆E
k0x
![]() (
C∆E
k).
(
C∆E
k).
2)
x
![]() (
C∆E
k)
x
C∆E
k0
x
(
C∆E
k)
x
C∆E
k0
x![]() ,
xE
k0
x
C∆E
k0
, x∆,
x
,
xE
k0
x
C∆E
k0
, x∆,
x![]() Ek
Ek
x
C∆(![]() Ek)
xA.
Ek)
xA.
Т.к. E k измеримо, то C∆E k измеримопо т.1а) измеримо измеримо.
Следствие: Если F замкнуто, то оно измеримо.
Доказательство: Пусть Fограниченное замкнутое множество.
=inf F, =sup F.
Т.к.
Fзамкнуто,
то E,
E,
причем xF:
xF[]=![]() .
.
Рассмотрим C∆F:
F=

C∆F=измеримо
F
измеримо.
C∆F=измеримо
F
измеримо.F
 G=
C∆Fоткрытое
множество.
G=
C∆Fоткрытое
множество.
Если x0G x0F x0 не является предельной для F(x0-, x0+)G
x0внутренняя для G Gоткрыто Gизмеримо C∆Gизмеримо.
Т.о. C∆Gизмеримо, но C∆G= F Fизмеримо.
Теоремы о расширении и о сгущении множества.
Теорема 1. (о расширении множества) Пусть заданы множества
E1,…, E n,…: E1… E n…. Если E k измеримо, то kN
E=
![]() Ek
mE =
Ek
mE =
![]() m Ek,.
m Ek,.
Доказательство:
1.
Пусть
A1=E1,
A2=E2\E1,
A3=E3\E2,…,
A k=E
k\E
k-1.
Покажем,
что
![]() Ak=E.
Ak=E.
A=
 Ak=E
Ak=EA kA m=, k m
1)
a) AE.
A k=E
k\E
k-1
A k
E k
kN![]() Ak
Ak
![]() Ek
AE
Ek
AE
б) EA. xE xA1 xE1 xA1 xA xE k, k2, E kмножество
с наименьшим номером, которому принадлежит x, т.е. xE1,…,E k-1
x E k\ E k-1=A kxA.
Из а), б) A=E
2) mkkm-1E kE m-1. Т.к. A k=E k\E k-1A kE k A kE m-1
A m=E k\E m-1A m и A k не имеют общих элементов, т.е. A kA m=, k m.
2.
A
kизмеримоk
(по следствию 1)
по т.1.б) E
измеримо и mE=![]() mAk=
mAk=
=![]() m(Ek\E
k-1)+mE1=
m(Ek\E
k-1)+mE1=![]() (mEk-mE
k-1)+
mE1=lim
(
(mEk-mE
k-1)+
mE1=lim
(![]() (mEk-mE
k-1)+mE1=
(mEk-mE
k-1)+mE1=
=![]() .
.
m (E k\E k-1)?
E k=A kE k-1, A kE k-1=. mE k=mA k+ mE k-1 mA k= mE k- mE k-1.
Теорема 2. (о сгущении множества) Пусть множества E1,…, E n ,…
измеримы:
E1…
E
n…,
E=![]() EnmE=
EnmE=
![]() .
.
Доказательство:
Пусть
E
k()=![]() kN.
Рассмотрим
C∆E
k.
kN.
Рассмотрим
C∆E
k.
Покажем,
что C∆E
k=![]() C∆(
E
n)=
C∆(
E
n)=![]() C∆E
n.
C∆E
n.
x C∆(
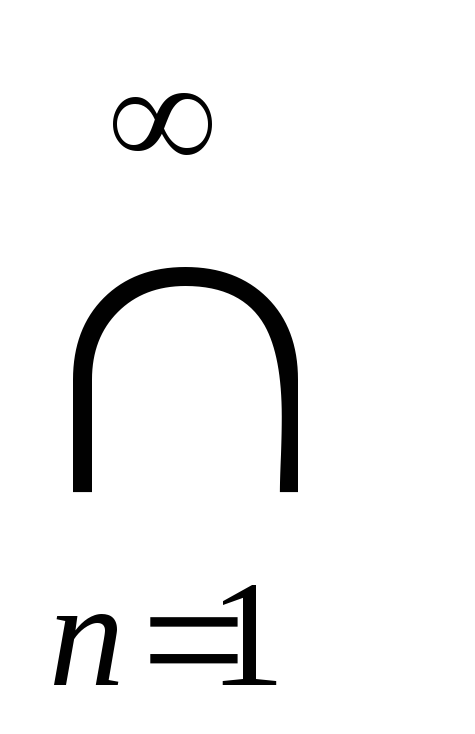 E
n)x
E
n)x ,
x
,
x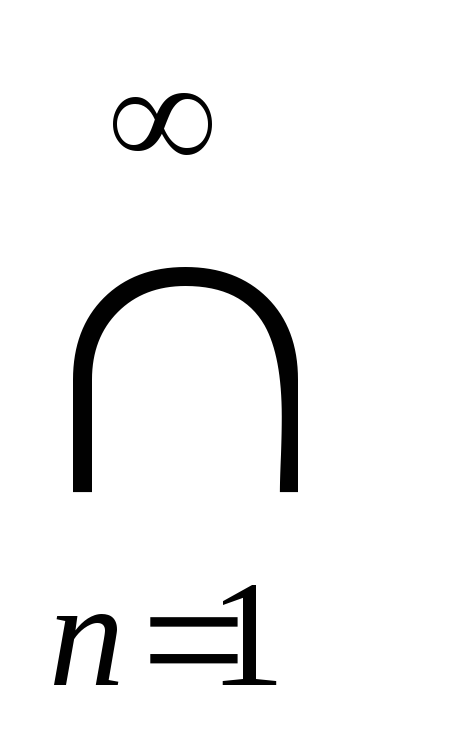 E
n
x
E
n
x , x
E
k0
x
, x
E
k0
x ,
x
C∆E
k
,
x
C∆E
k
x![]() C∆E
n.
C∆E
n.
б)
x![]() C∆E
n
x
C∆E
n
x![]() C∆E
k0
(k0N)
x
, x E
k0
x
∆,
x
C∆E
k0
(k0N)
x
, x E
k0
x
∆,
x![]() En
En
x
C∆(
![]() En).
En).
Т.к. E1… E n… C∆E 1… C∆E n. Т.к. E k измеримо, то C∆E k измеримо.
По т.1. можем утверждать:
C∆E измеримо
mC∆E=
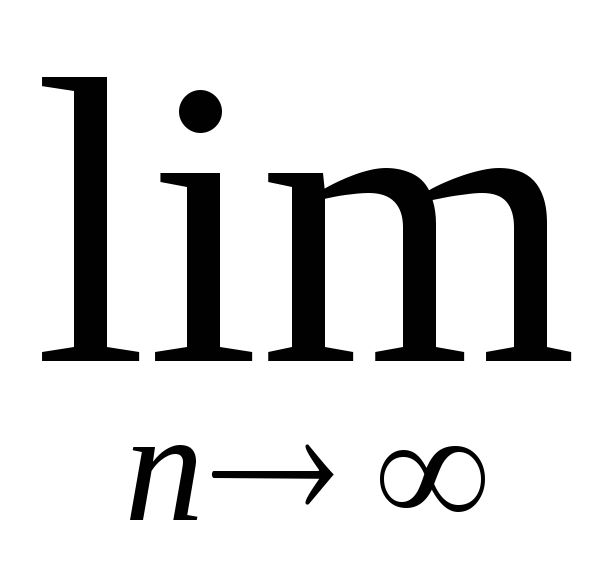 mC∆E
n
mC∆E
n
По
лемме 3 E
измеримо mE
+ m(C∆E)=-=![]()
--mE=![]() ((-)-mE
k)
((-)-mE
k)
mE=![]() mE k.
mE k.
