
![]() Полные
метрические пространства.
Полные
метрические пространства.
Фундаментальные последовательности.
Опр.1. Последовательность точек (x n) M называется фундаментальной,
если N: n, m > N x n , x m <.
Заметим, что если n=m x n , x m)= x n , x n )=0<.
Пусть n m , m > n , m = n + p , pN.
Опр.2. Последовательность точек (x n) M называется фундаментальной,
если N: n > N pN x n+p , x n <.
Теорема 1. Пусть - метрическое пространство. .
x n )последовательность точек из Е.
Из фундаментальности последовательности x n) в одном из
пространств следует фундаментальность ее в другом прос-
транстве.
Доказательство обозначим метрику в пространстве через , а в
пространстве . Очевидно, что x , y x , y)= x , y).
Последовательность x n ) фундаментальна в Е N: n, m > x n , x m <.
x n x n N: n, m > x n , x m < ( x n ) фунда-
ментальна в .
Теорема 2. Всякая фундаментальная последовательность ограничена.
Доказательство пусть (x n)любая фундаментальная последователь-
ность N: n, m > N x n , x m <.
Пусть , m0fic,m0>N n>N x n , x m0 <1.
Рассмотрим x 1 , x m0) , x 2 , x m0) ,…, x , x m0) ,1.
max { x 1 , x m0), x 2 , x m0), …, x , x m0) ,1}.
nN x n , x m0 K по определению (x n) ограничена.
Теорема 3. Всякая сходящаяся последовательность фундамен-
тальна.
Доказательство
![]() x
n
=a
x
n
=a![]() N:
n>N
x
n
, a
<
N:
n>N
x
n
, a
<![]() .
.
pN
n + p>N:
x n
+ p
, a <![]() .
.
>0
N:
n>N
pN
x n
+ p
, x n
<
x n
+ p
, a )+
a , x n)<![]() +
+![]() .
.
По определению последовательность является фундаментальной.
Не всякая фундаментальная последовательность элементов метрического
пространства является сходящейся в данном пространстве.
Пр.1. Рассмотрим =(0,1) с метрикой =x-y, x , y.
Рассмотрим
последовательность (![]() ).
).
x
n
, x
m)=x
n-x
m=(![]() )
- (
)
- (![]() )
)![]() 0
по определению
0
по определению
(![]() )
фундаментальная последовательность.
)
фундаментальная последовательность.
![]() =0последовательность
(
=0последовательность
(![]() )
в пространстве
)
в пространстве
сходящейся не является.
Пр.2. Пусть пространство многочленов с действительными коэффи-
циентами n(t)=a n t n + a n-1 t n-1+…+a0, t[0,1] с метрикой
(p
n
,
q m
)=![]() p
n
(t)-q
m
(t).
Возьмем
последовательность (P
n
(t)):
p
n
(t)-q
m
(t).
Возьмем
последовательность (P
n
(t)):
P
n
(t)=
![]() .
.
Оценим
(p
n
+ s (t)-p
n
(t))=
![]()
p n
+ s (t)-p
n
(t)
=
p n
+ s (t)-p
n
(t)
=![]()
![]() =
=
=![]()
![]() =
=![]() .
.
![]() сходится
сходится
![]() R
n=0
R
n=0![]()
![]() =0.
=0.
(P n (t)) фундаментальная последовательность.
Решим вопрос о ее сходимости.
![]() P
n
(t)=
P
n
(t)=
![]() =et(P
n
(t))
не сходится в пространстве многочленов.
=et(P
n
(t))
не сходится в пространстве многочленов.
В связи с примерами 1 и 2 дадим определение:
Опр.3. Метрическое пространство называется полным, если в нем вся-
кая фундаментальная последовательность сходится к некоторому
пределу, являющемуся элементом этого пространства.
Примеры полных метрических пространств.
1. Пространство R полно.
Доказательство: критерий Коши.
2. R n полное пространство.
Это следует из полноты пространства R.
Пусть (x(p)) фундаментальная последовательность точек пространства R n,
т.е. x(p)=(x1(p), x2(p),…, x n(p)).
x(q)=(x1(q), x2(q),…, x n(q)).
N
p,
q>N (x(p),x(q))=![]() <.
<.
Очевидно, что i=1,…,n будет выполняться неравенство
x i (p)-x i (q)< (x i (p)) фундаментальна (x i (p)) сходится
![]() x i
(p)=x
i
, i=1,…,p.
x i
(p)=x
i
, i=1,…,p.
Рассмотрим кортеж x=(x1,x2,…,x n).
Очевидно:
каждое x i RxR n
lim x(p)=x (т.к. сходимость последовательности точек из R n понима-
ется как сходимость по координатам).
Таким образом, пространство R n полно.
3. Пространство C [a , b] полно.
Сходимость по метрике последовательности точек пространства C [a , b]
есть равномерная сходимость последовательности непрерывных функций.
Пределом такой последовательности является непрерывная функция, т.е.
элемент пространства C [a , b] C [a , b] полно.
4.Пространство m полно.
m пространство всех ограниченных последовательностей действитель-
ных
чисел с метрикой (x,y)=![]() x
i
–y
i.
x
i
–y
i.
mметрическое пространство. Докажем его полноту.
Пусть (x(n)) - фундаментальная последовательность точек пространства m.
Это
означает, что
N
n,
m>N
(x(n),x(m))=
![]() x
i
(n)-x
i
(m)<.
x
i
(n)-x
i
(m)<.
Тем более (1) iN x i (n)-x i (m)< {x i (n)} фундаментальная по критерию Коши она сходится на R,т.е. lim x i(n) =x i iN.
Рассмотрим кортеж x=(x1,x2,…,x n).
Очевидно:
1)
![]() x(n)=x
(x(n),x)<
x(n)=x
(x(n),x)<
![]() x
i
(n)-x
i
<.
x
i
(n)-x
i
<.
Это
будет верно, т.к.
![]() x
i(n)
=x
i
,т.е.
x
i
(n)-x
i
<
x
i(n)
=x
i
,т.е.
x
i
(n)-x
i
<
![]() x
i
(n)-x
i
<.
x
i
(n)-x
i
<.
2)xm
Покажем, что последовательность является ограниченной. При n
x i -x i(m) iN (взяли предел от левой и правой частей равенства (1)
и
воспользовались тем, что
![]() x
i(n)
=x
i)
x
i(n)
=x
i)
x i(m)x i x i(m)+.
Отсюда получаем, что x ограничено, т.к. все его члены x i ограничены
(т.к. (x i(m)) фундаментальна она ограничена x=(x i) ограничена по определению) xm.
Из 1) и 2) следует, что m полно.
5. Пространство L2 полно.
L 2пространство последовательностей действительных чисел x=(x n), т.ч.
ряд
![]() сходится.
сходится.
L
2метрическое
пространство с метрикой
![]()
Докажем полноту L 2.
Пусть (x n) фундаментальная последовательность точек пространства L 2.
(x n)=(x1(n),x2(n),…x k(n),…).
N
n>N
pN
![]() (2)
(2)
Тем более iN x i(n)-x i(n+p)< (x i(n)) фундаментальна (x i(n)) схо-
дится,
т.е.
![]() x
i(n)
=x
i
iN.
x
i(n)
=x
i
iN.
Рассмотрим кортеж x=(x1,x2,…,x n).
Покажем, что xL 2.
Зафиксируем NN и рассмотрим
![]()
Оценим каждое из слагаемых. Из (2) для =1 N n>N pN
![]() .
Тем более
.
Тем более
![]() .
.
Перейдем в этом неравенстве к пределу при p:
![]() .
.
Оценим второе слагаемое.
Т.к.
x(n)L
2, то
![]() .
.
Т.о.
![]() .
.
Перейдем к пределу при N и получим:
![]() .
.
Докажем, что
 N:
N:
(x
(n),x)=
![]()
Из
(2)
![]()
Перейдем к пределу при p:
![]()
Перейдем к пределу при N и получим:
![]()
По
определению
![]()
L2
полно.
L2
полно.
![]()
Линейные нормированные пространства.
Пусть множество, в котором
введена операция, ставящая в соответствие каждой паре элементов
(x , y) элемент из , называемый суммой этих элементов и обозна-
чаемый x+y, причем выполнены следующие аксиомы:
x, y, z
1) x + y=y + x (коммутативность сложения)
2)(x + y) + z=x + (y + z) (ассоциативность сложения)
3) элемент, обозначаемый 0, называемый нулевым элементом или
нулем, т.ч. x x+0=x
4)x соответствует единственный противоположный элемент из ,
обозначаемый -x т.ч. x+(-x)=0
x+(-y)=x-y
2.введена операция умножения элементов из на число из R(C),
удовлетворяющая следующим аксиомам:
x, y, , R(C):
5)x)=()x (ассоциативность умножения)
6)(x + y)=x + y (дистрибутивность умножения)
7)()x=x+x (дистрибутивность умножения)
8)1*x=x
Опр.1. Множество с операциями 1. и 2. , удовлетворяющими аксиомам
1)-8) называется линейным пространством над полем R(C).
Опр.2. Линейное пространство над полем R называется нормирован-
ным, если каждому элементу x поставлено в соответствие
действительное число, называемое нормой x и обозначаемое
![]() ,
удовлетворяющее следующим аксиомам
нормы:
,
удовлетворяющее следующим аксиомам
нормы:
x , y R
 ,,
причем
,,
причем
 =0
x=0
=0
x=0
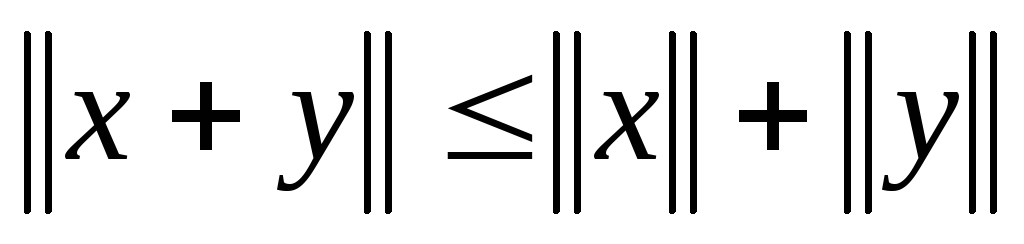
Теорема. Всякое нормированное пространство является метрическим с
Метрикой (x
, y)=![]() .
.
Доказательство: Пусть нормированное пространство. Докажем, что
функция
(x
, y)
=![]() задает метрику на.
Для этого проверим спра-
задает метрику на.
Для этого проверим спра-
ведливость аксиом 1.-3. метрического пространства.
(x , y)=0 x=y
(x ,
y)=0
![]() =0
x-y=0
(x-y)+y=0+y
x+(- y + y)=y
=0
x-y=0
(x-y)+y=0+y
x+(- y + y)=y
x+0=y x=y
(x , y)= (y , x)
(x , y)
=![]() =
=![]() =
=![]() =
=![]() =(y
, x)
=(y
, x)
(x , y) (x , z) + (z , y)
(x , y)
=![]() ==
==![]() =(x
, z) + (z
, y).
=(x
, z) + (z
, y).
На нормированные пространства переносятся многие понятия и их
свойства, справедливые для метрических пространств, в частности имеется понятие сходимости последовательности.
Опр.3.Последовательность (x n), x n называется сходящейся к x, если
lim (x
n
,x) =![]() =0
NN
n>N
=
=0
NN
n>N
=![]() <.
<.
Опр.4. Последовательность (x n), x n называется фундаментальной, если
NN
n,
m>N =![]() <.
<.
Опр.5.Нормированное пространство называется полным, если любая
фундаментальная последовательность его точек сходится к точке
этого же пространства. Полное нормированное пространство назы-
вается банаховым пространством.
Структура открытых линейных множеств на R.
Пусть линейное множество.
Опр.1. Множество R называется ограниченным сверху (снизу), если
такая точка Q (P), что x xQ (xP).
Опр.2. Множество R называется ограниченным, если оно ограничено
снизу и сверху, т.е. если Q, PR: x PxQ.
Опр.3. Множество R называется ограниченным, если x
x .
Опр.2.Опр.3.
Опр.4. Точка R называется верхней гранью множества , если пра-
вее точки нет точек множества и x, лежащая
правее точки .
Обозначается
=sup
E=
![]()
Опр.5. Точка mR называется нижней гранью множества , если левее
точки m нет точек множества и x, лежащая левее
точки m+.
Обозначается
m=inf
E=
Теорема 1. Всякое непустое ограниченное сверху (снизу) множество
Имеет верхнюю (нижнюю) грань.
Теорема 2. Если верхняя (нижняя) грань множества существует, но не
принадлежит , то она является предельной точкой множест-
ва .
Доказательство: Пусть =sup E, . Докажем, что предельная точка множества . Возьмем любую окрестность точки V(M,).
Возьмем : V(M,). Т.к. =sup E, то x x (x)
x V(M,). По определению предельная точка множества .
Доказательство аналогично в случае m=inf E.
Следствие 1. Если замкнутое множество ограничено сверху (снизу),
то оно имеет самую правую (левую) точку.
Доказательство: Пусть =sup E. Возможны два случая:
1.
2.
Если выполняется 1., то по теореме 2 следует, что предельная точка
множества , но замкнуто , что противоречит условию, т.е.
случай 1 не возможен. Т.о. =sup E и , т.е. самая правая точка
множества .
Доказательство аналогично в случае m=inf E.
Следствие 2. Если ограниченное замкнутое множество, то существует
наименьший отрезок, содержащий . Им является отрезок
[m , M].
Лемма 1. Множество попарно непересекающихся интервалов на R или
конечно, или счетно.
Доказательство: Пусть множество попарно непересекающихся ин-
тервалов на R . Qсчетное множество рациональных чисел. Представим его в виде бесконечной последовательности, т.е. Q={r1,r2,…,r n,…}. Возьмем . На существует бесконечно много рациональных чисел . Пусть r n1 одно из них. Соответствующий интервал обозначим n1.
Для числа r n2 поставим в соответствие интервал, которому он принадле-
жит: r n2 n2. И т.д. Очевидно, что r n1 r n2 n1n2. Число интервалов
равно числу натуральных чисел n1, n2,… . Множество, состоящее из
натуральных чисел либо конечно, либо счетно, но (n1, n2,…)
А либо конечно, либо счетно.
Опр.6. Пусть Gоткрытое множество. Интервал (a ,b) называется состав-
ляющим интервалом множества G, если (a ,b)G, а его концы
a и b не принадлежат G.
Теорема 3. Если G непустое, ограниченное, открытое множество, то
каждая его точка принадлежит некоторому его составляю-
щему интервалу.
Доказательство: возьмем x0G. Покажем, что она принадлежит неко-
торому его составляющему интервалу. Рассмотрим множество
F=CG[x0, +).
F замкнуто (CG замкнуто, [x0, +) замкнуто их пересечение замкну-
то).
F - ограничено снизу (x0нижняя граница)=inf F.
Поскольку F замкнуто и предельная точка множества F, то по
теореме 2 F.
Возьмем x0 и выясним, где будет .
F CGGx0, [x0, +)x0x0.
Рассмотрим промежуток [x0 , ). Покажем, что [x0 , )G.
Предположим, что [x0 , )G. x[x0 , ): x G xCG, x[x0,)
xF, но x<M. Что не возможно, т.к. =inf F.
Доказали, что [x0 , )G.
Аналогично строится промежуток (m , x 0]G, m=sup (CG( , x 0]).
Итак, (m , x 0] [x0,)=(m , M)G, m, MG, x0(m ,M).
Теорема 4 (о строении ограниченного открытого множества).
