Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брянский государственный университет им. академика И.Г. Петровского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

измеримые функции

.doc

Скачиваний:

131

Добавлен:

30.05.2015

Размер:

632.32 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

§26. Измеримые функции

Пусть Е - измеримое множество, ЕR и задана функция f, область определения которой содержит Е.

Определение. Функция называется измеримой на , если множество измеримо.

Теорема 1. Пусть Е измеримо, f задана на Е. Функция f измерима тогда и только тогда, когда  АR одно из множеств 1-3 измеримо:

1. Е(f ≤ A);

2. E(f ≥ A);

3. E(f < A).

Доказательство:

1. f измерима  E(f ≤ A) измеримо.

) f измерима  по определению E(f > A) измеримо АR. E(f ≤A)=E\E(f>A). По следствию из теоремы 2(а) множество E(f ≤ A) измеримо как дополнение измеримого множества до Е.

)Пусть E(f ≤ A) измеримо  E(f > A) = E\E(f ≤ A) измеримо, следовательно, по определению f измерима.

2. f измерима  E(f ≥ A) измеримо.

) f измерима. Докажем, что E(f≥A) измеримо.

Покажем методом встречных включений, что .

а) x_o E(f≥A)  f(x_o)≥A  nN  nN  .

b)  n N  n N. Переходя к пределу при n, получим, что f(x_o)≥A  x_o  E(f ≥ A).

Так как f измерима, то измеримо n N. Следовательно, по теореме 2(б) измеримо.

) E(f≥A) измеримо. Докажем, что f измерима.

Рассмотрим множество E(f > A). Покажем, что .

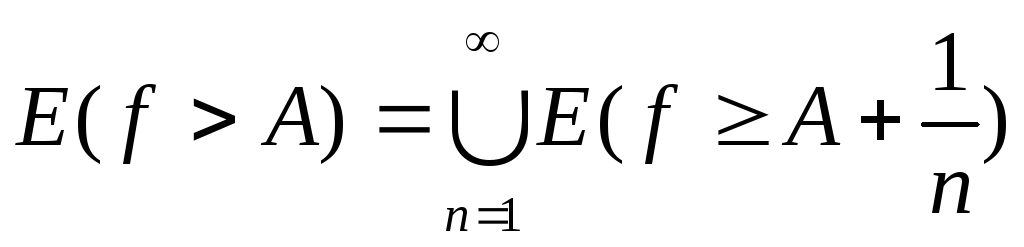a) Пусть x_oE(f>A)  f(x_o) >A. Очевидно, что n_oN:   x_o.

b) x_o , n_o  N  f(x_o)>A  x_oE(f>A).

По условию измеримо nN и по теореме 1(а) множество E(f>A) измеримо  f по определению измерима.

3. Провести доказательство самостоятельно.

§27. Арифметические действия над измеримыми функциями

Теорема 2. Пусть f и g - измеримые функции. Тогда множество E(f >g) = {xE: f(x)>g(x)} измеримо.

Доказательство:

Занумеруем рациональные числа . Покажем методом встречных включений, что .

а) Пусть x_oE(f>g)  f(x_o) > g(x_o).

  Q : f(x_o)>>g(x_o)  f(x_o)>и g(x_o)< x_oE(f >) и x_oE(g <)  x_oE(f>)E(g<)  x_o.

б) Пусть x_o   n_oN : x_oE(f >) и x_oE(g <)  f(x_o)>и g(x_o)< f(x_o)>g(x_o)  x_oE(f>g).

Так как f измерима, то E(f >) измеримо nN. Так как g измерима, то E(g <) измеримо nN. Следовательно, по теореме 2 множество E(f >)E(g <) измеримо nN, следовательно, по теореме1(а) множество E(f >g) измеримо.

Теорема 3. Пусть функции f и g определены на измеримом множестве Е.

1) Если f измерима, k,rR, то функции kf и f +r измеримы на Е.

2) Если f и g измеримы на Е, то f ± g измерима на Е и fg измерима на Е.

3) Если f(х)≠0 хЕ, то 1/f ,g/f – измеримые функции на Е.

Доказательство:

1. а) Докажем, что функция kf измерима на Е, то есть что множество Е(kf >A) измеримо АR.

Рассмотрим неравенство kf >A.

Пусть k=0. Имеем 0>A  E(0>A)={xE: 0>A}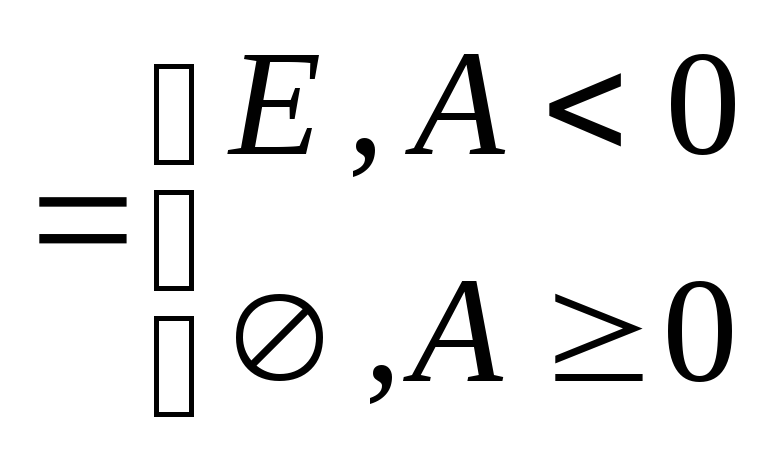 - измеримо, так как Е и  - измеримые множества. Следовательно, функция kf измерима при k=0.

Пусть k≠0, тогда

- измеримо, так как f измерима  kf измерима.

б) Докажем, что f+r измерима на Е.

f+r – измерима на Е  множество E(f+r>A) измеримо, но E(f+r>A)=E(f>A-r) измеримо (так как f измерима, ).

2. а) Докажем, что f±g измерима на Е.

f±g – измеримая функция  множество Е(f ±g >A) AR измеримо.

Е(f±g>A)=Е(f >Ag), но функция (–g) измерима по пункту 1) данной теоремы, функция Аg измерима по тем же соображениям  по теореме 2 множество Е(f>Ag) измеримо  f±g измерима.

б) Докажем, что fg измерима на Е.

Пусть . Докажем, что f ² измерима на Е, то есть множество Е(f²>A) измеримо АR.

E(f²>A) .

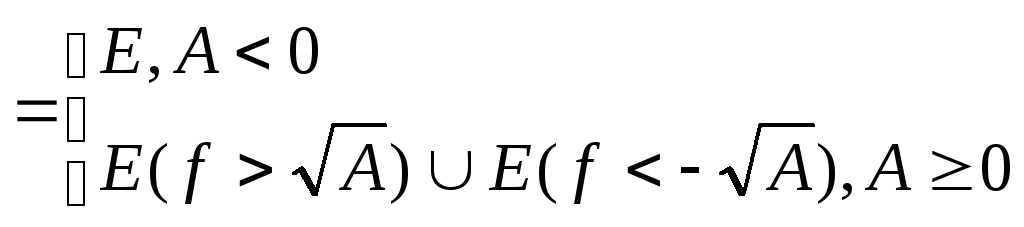Очевидно, что и Е - измеримые множества, то есть множество Е(f²>A) измеримо АR.

Пусть далее . Заметим fg=. Так как f±g – измеримые функции, то функции (f±g)² также измеримы  - измеримая функция, то есть fg – измеримая функция.

3. а) Докажем, что - измеримая функция на Е, то есть множество измеримо АR.

Пусть А=0, тогда .

П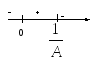усть А≠0, тогда .

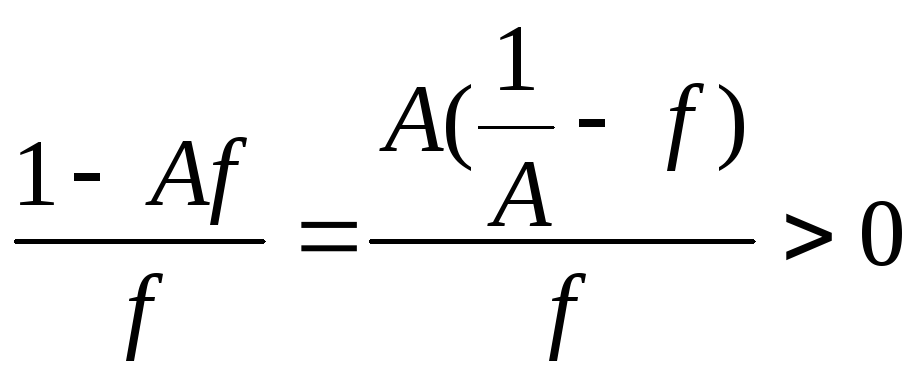Если А>0, то 0<f(x)<.

Если А<0, то f(x)< или f(x)>0.

Таким образом,

- измеримо АR.

б) Докажем, что - измеримая функция на Е.

измерима на Е, так как функции и измеримы.

§28. Интеграл Лебега

Пусть Е – измеримое множество, - измеримая функция на Е. Будем предполагать, что ограничена на Е, то есть существуют , такие, что . Разобьем на части точками , ,…,. Разбиение обозначим : . Каждому полученному промежутку будет соответствовать множество

=, .

Составим суммы: , , которые назовём нижняя и верхняя суммы Лебега.

Свойства множеств .

1. , ;

2. - измеримо (так как - измерима);

3. ;

4. (из 1-3).

Очевидно, что (из определения).

Упражнение. Доказать самостоятельно свойства 1-4.

Определение. Функция суммируема или интегрируема по Лебегу, если при любом разбиении этого отрезка, где . Общее значение этих пределов называется интегралом Лебега от функции на множестве Е и обозначается .

Таким образом,

Свойства сумм Лебега

Теорема 1. Пусть - некоторое разбиение отрезка , то есть . Разбиение получается из Т добавлением новых точек, то есть ; , - суммы Лебега, соответствующие разбиению Т; , - суммы Лебега, соответствующие разбиению . Тогда , .

Доказательство:

Доказательство достаточно провести для случая добавления одной точки, то есть , .

, где .

Множество разбиваем на два множества: ; . Тогда ; . Следовательно,

;

Так как , то . Аналогично доказывается, что .

Теорема 2. Для произвольных разбиений Т и , (любая нижняя сумма Лебега не превосходит любой верхней).

Доказательство:

Рассмотрим разбиение . Так как можно получить из Т добавлением новых точек из , то по теореме 1 , (1).

С другой стороны, , то есть его можно получить из добавлением новых точек из Т. Тогда по теореме 1, , (2). Кроме того, (3).

Из (1), (2), (3) следует, что , .

Теорема 3. Пусть Е – измеряемое множество и

1) ограничена на множестве Е;

2) измерима на Е.

Тогда существует .

Доказательство:

Множество ограничено сверху, так как , следовательно, существует . Множество ограничено снизу, следовательно, существует . Докажем, что . , так как s, S: . Пусть - некоторое разбиение , и - нижняя и верхняя суммы Лебега, соответствующие данному разбиению. Тогда