
- •§12. Функции и их общие свойства
- •1. Отображение. Виды отображений
- •2. Сужение функций
- •3.Действительная функция действительного переменного
- •4.Способы задания функции
- •5. Равенство функций. Арифметические действия над функциями
- •6.Сложная функция (композиция функций)
- •§13. Простейшая классификация функций
- •1. Ограниченные и неограниченные функции
- •2.Четные и нечетные функции
- •3. Периодические функции
- •4. Монотонные и кусочно-монотонные функции
- •§14. Обратная функция
- •§15. Предел функции
- •1. Предельная точка множества
- •2. Первое определение предела функции в точке (по Гейне)
- •3. Второе определение предела функции (по Коши).
- •Если , то; если, то; если, то.
- •§ 16. Односторонние пределы
- •§ 17. Распространение теорем о пределах
- •§ 18. Некоторые замечательные пределы
- •§19. Бесконечно малые и бесконечно большие функции
- •§20. Сравнение бесконечно малых функций и бесконечно больших функций
§12. Функции и их общие свойства
1. Отображение. Виды отображений
Пусть X={x}, Y={y}- произвольные множества.
Определение 1. Отображением множества Х во множество Y (или функцией, определенной на Х со значениями в Y) называется соответствие f, которое каждому элементу xX соотносит единственный элемент yY, обозначаемый y=f(x).
Элемент y=f(x) называется образом элемента x при отображении f или значением функции f.
Обозначается
f:
X![]() Y
или X
Y
или X
![]() Y.
Y.
X- множество, где определена функция, называется областью определения функции.
Образом
множества
А![]() X
при отображении f
называется множество f(A)={yY:y=f(x),
xА}.
Множество f(X),
т.е. образ множества X
называется множеством
значений функции
(отображения).
X
при отображении f
называется множество f(A)={yY:y=f(x),
xА}.
Множество f(X),
т.е. образ множества X
называется множеством
значений функции
(отображения).
Определение
2. Отображение
множества X
во множество Y
называется отображением
X
в
Y,
если f(Х)![]() Y.
Y.
Определение
3. Отображение
множества X
во множество Y
называется отображением
X
на
Y
(или сюрьективным
отображением),
если f(Х)=Y
т.е. отображение f
сюрьективно, если
![]() yY
yY
![]() xX:
f(x)=y.
xX:
f(x)=y.

Возьмём
![]() yf(X)
yf(X)
![]() xX:
f(x)=y.
Этих элементов может быть несколько.
Множество всех xX,
таких что f(x)=y
называют полным
прообразом
элемента y
при отображении f
и обозначают
f
-1(y),
xX:
f(x)=y.
Этих элементов может быть несколько.
Множество всех xX,
таких что f(x)=y
называют полным
прообразом
элемента y
при отображении f
и обозначают
f
-1(y),
т.е. f -1(y)={xX: f(x)=y}.
О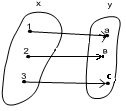 пределение
4. Отображение
f:X
пределение
4. Отображение
f:X![]() Y
называется инъективным
(обратимым),
если yY
его полный прообраз f
-1(y)
состоит не более, чем из одного элемента.
Y
называется инъективным
(обратимым),
если yY
его полный прообраз f
-1(y)
состоит не более, чем из одного элемента.
Определение
4.
Отображение f:X![]() Y
называют инъективным,
если различным элементам хХ
соответствует различные элементы yY,
т.е.
Y
называют инъективным,
если различным элементам хХ
соответствует различные элементы yY,
т.е.
![]() x1,
x2Х:
x1
x2
f(x1)f(x2).
x1,
x2Х:
x1
x2
f(x1)f(x2).
Определение
5. Отображение
f:X![]() Y
называется взаимно-однозначным
(или биективным),
если оно инъективно и сюрьективно. Таким
образом, отображение f:X
Y
называется взаимно-однозначным
(или биективным),
если оно инъективно и сюрьективно. Таким
образом, отображение f:X![]() Y
взаимно-однозначно, если
Y
взаимно-однозначно, если
![]() yY
его полный прообраз состоит только из
одного элемента.
yY
его полный прообраз состоит только из
одного элемента.
2. Сужение функций
Пусть функция y=f(x) задана на множестве X.
Пусть
А![]() X.
Тогда отображение f
естественным образом порождает
отображение (функцию), определённую на
А и ставящую в соответствие
X.
Тогда отображение f
естественным образом порождает
отображение (функцию), определённую на
А и ставящую в соответствие
![]() xА
элемент f(x)=y.
Эту новую функцию называют сужением
функции f
на множестве А
xА
элемент f(x)=y.
Эту новую функцию называют сужением
функции f
на множестве А![]() X
и обозначают fА.
Таким
образом, fА:
А
X
и обозначают fА.
Таким
образом, fА:
А![]() Y,
fА(x)=f(x)
Y,
fА(x)=f(x)
![]() xА.
xА.
Пример.
y=f(x)=sinx,
x![]()
А=[0;2π]
y=fА(x)=sinx, x[0;2π]- сужение.
3.Действительная функция действительного переменного
Определение.
Действительной
функцией действительного переменного
называется функция f:X![]()
![]() ,
где X
,
где X![]()
![]() .
Элемент x
называется аргументом функции f
(или независимой переменной), элемент
y=f(x)
.
Элемент x
называется аргументом функции f
(или независимой переменной), элемент
y=f(x)![]() -
зависимой переменной.
-
зависимой переменной.
Такие функции называют числовыми. Название ДФДП связано с тем, что x и y - действительные переменные, принимающие действительные значения.
Множество, на котором определена функция, называется областью определения и обозначается D(f). Множество ее значений обозначается Е(f).
Таким образом, для задания функции f необходимо задать ее область определения и закон f, по которому каждому элементу xD ставится в соответствие определенное число y.
4.Способы задания функции
Существует несколько способов задания функции.
1. Аналитический способ.
При этом соответствие f задано с помощью формулы (аналитического выражения), указывающей, какие действия и в каком порядке надо совершить над аргументом x, чтобы получить соответствующее значение функции.
Например,
y=sin
x3
+![]() ,x
,x .
.
Одно
и то же аналитическое выражение может,
определять различные функции, если они
заданы на различных множествах, т.е.
имеют разные D(f).
Если функция задана формулой и не указана
D(f),
то считают, что функция задана на
множестве тех значений, аргумента x![]() ,
для которых формула имеет смысл.
,
для которых формула имеет смысл.
П![]() ример
1. y=f(x)=
ример
1. y=f(x)=
![]() .
НайтиD(f)
.
НайтиD(f)
![]() D(f):
D(f):
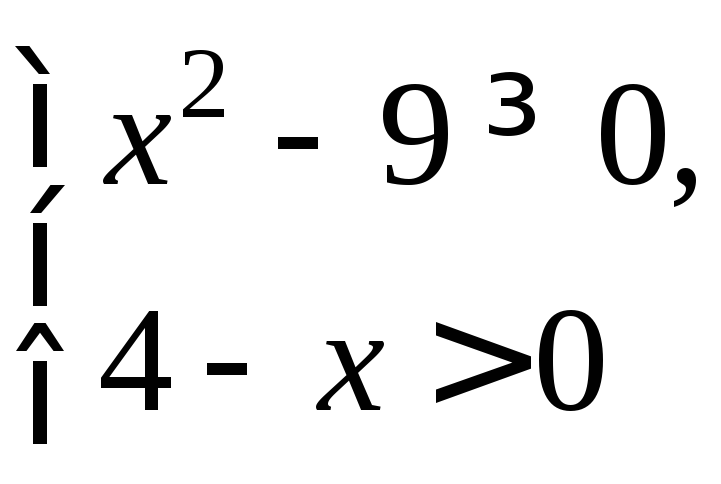
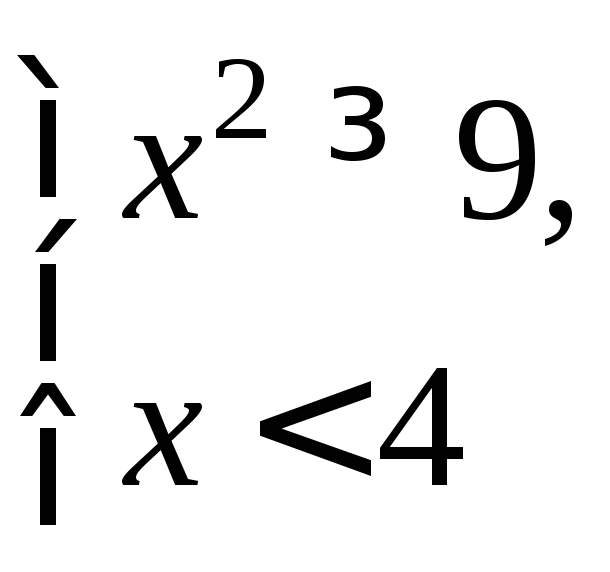
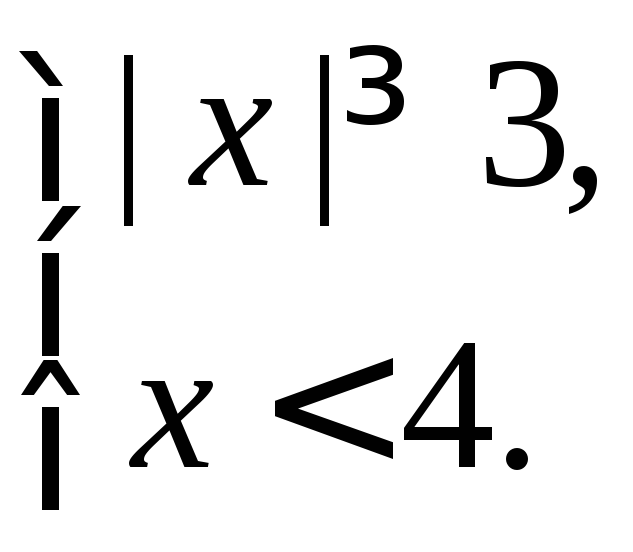
З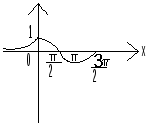 начит,D(f)=(-∞;-3]
начит,D(f)=(-∞;-3]![]() [3;4).
[3;4).
![]()
Функция
может быть задана различными формулами,
например,
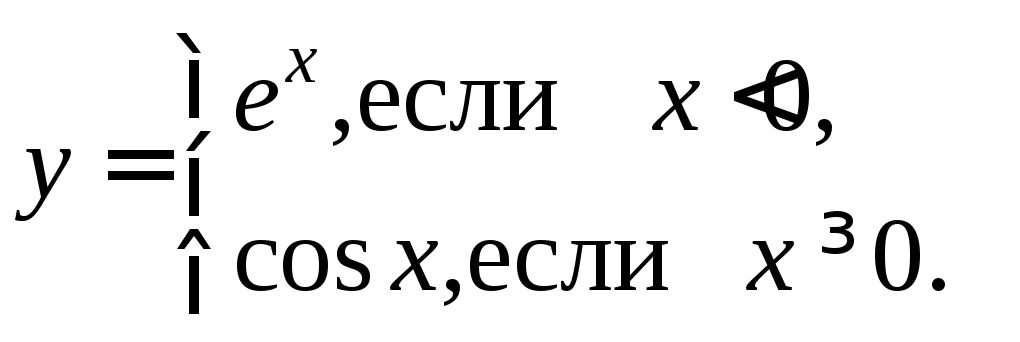
2. Словесное задание функций.
Пример 2. y= π(x)- функция, ставящая каждому значению x в соответствие количество простых чисел, не превосходящих его.
π(7)=4 (2,3,5,7)
π(![]() )=5 (2,3,5,7,11)
)=5 (2,3,5,7,11)
Пример
3.
 (signum
– знак)
(signum
– знак)
Пример
4. Функция
Дирихле
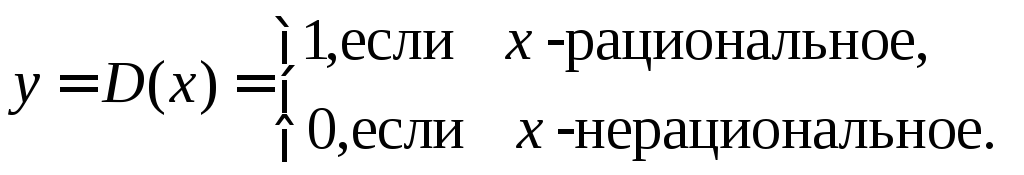
3. Табличный способ.
При этом способе выписываются значения независимой переменной x и соответствующие им значения функции.
|
х |
x1 |
x2 |
x3 |
… |
xn |
|
y |
f(x1) |
f(x2) |
f(x3) |
… |
f(xn) |
Достоинство: легко найти значение функции в нужной точке.
Недостатки: 1) конечность D(f) (невозможность отыскать промежуточные значения аргумента), 2) малая наглядность.
4. Графический способ.
Координатная
плоскость -
обычная геометрическая плоскость с
выбранной на ней прямоугольной системой
координат. Множество всех упорядоченных
пар действительных чисел называется
числовой
плоскостью
и обозначается
![]() ,
а отдельные пары чисел - ее точками,
{(x,y)}=
,
а отдельные пары чисел - ее точками,
{(x,y)}=![]() .
Между координатной плоскостью и числовой
плоскостью можно установить
взаимно-однозначное соответствие:
М(x,y)
.
Между координатной плоскостью и числовой
плоскостью можно установить
взаимно-однозначное соответствие:
М(x,y)
![]() (x,y),
где М(x,y)-
произвольная точка координатной
плоскости, (x,y)-
точка числовой плоскости
(x,y),
где М(x,y)-
произвольная точка координатной
плоскости, (x,y)-
точка числовой плоскости
![]() ,х,
у-
её координаты.
,х,
у-
её координаты.
Пусть
функция y=f(x)
задана на множестве D,
т.е. xD.
Задание функции равносильно заданию
множества пар чисел {(x,y):y=f(x),
xD}![]()
![]() .
.
И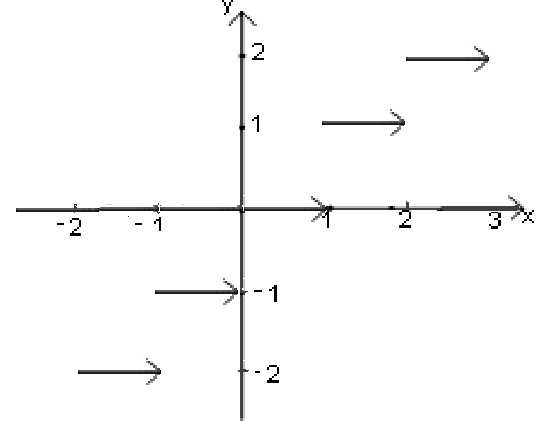 зобразим
его на координатной плоскости. Полученное
множество точек называется графиком
функции.
зобразим
его на координатной плоскости. Полученное
множество точек называется графиком
функции.
Определение. Графиком функции f называется множество точек координатной плоскости {M(x,y):y=f(x), xD}. Часто графиком функции является кривая.
Пример
5. y=[x]=E(x),
x![]() (антье от х)-
целая часть числа x,
(наибольшее целое число, не превосходящее
данного действительного числа).
(антье от х)-
целая часть числа x,
(наибольшее целое число, не превосходящее
данного действительного числа).
П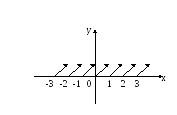 ример
6. y={x}=x-[x],
x
ример
6. y={x}=x-[x],
x![]() -дробная
часть числа x.
-дробная
часть числа x.
0![]() x<1 y=x,
x<1 y=x,
1![]() x<2 y=x-1,
x<2 y=x-1,
2![]() x<3 y=x-2,
x<3 y=x-2,
-1![]() x<0 y=x+1.
x<0 y=x+1.
Не
всякое множество точек координатной
плоскости является графиком функции.
Т.к. по определению функции
![]() xD
соответствует только одно значение y,
то любая прямая, параллельная оси Оy,
может пересекать график не больше, чем
в одной точке.
xD
соответствует только одно значение y,
то любая прямая, параллельная оси Оy,
может пересекать график не больше, чем
в одной точке.


Данные кривые не могут служить графиками функций.
Заметим, что график функций может состоять из кусков различных кривых, из отдельных точек.
Задание функции с помощью графика называется графическим способом задания функции.
Достоинство: наглядность (по графику можно судить о характере поведения функции).
Недостатки: 1)невозможно применить в должной мере математический аппарат,
2)приближённое построение чертежа.
3)построение чертежа для ограниченного множества точек.
