
- •Введение в анализ
- •§1. Действительные числа
- •1. Понятие действительного числа
- •2. Модуль действительного числа и его свойства Определение. Модулем действительного числа а называется неотрицательное число, обозначаемое |а|, определяемое формулой:
- •Геометрический смысл: Пример 1.А);
- •По свойству 3
- •Число хнаходится от точкиана расстоянии меньшем, чемb.
- •3. Числовые множества. Промежутки. Окрестности
- •§ 2. Ограниченные и неограниченные множества. Верхние и нижние грани числовых множеств
- •§ 3. Предел последовательности
- •2. Предел последовательности. Пусть дана последовательность :(1)
- •3. Единственность предела
- •4. Ограниченность сходящейся последовательности
- •Доказательство.
- •5. Свойства сходящихся последовательностей
- •§ 4. Бесконечно малые последовательности
- •§ 5. Бесконечно большие последовательности (ббп)
- •§ 6. Свойства пределов, связанные с арифметическими операциями над сходящимися последовательностями
- •3. Произведение .
- •§7. Предел монотонной последовательности (признаки существования предела последовательности)
- •§ 8. Принцип вложенных отрезков
- •§ 9. Число е.
- •§10. Подпоследовательности
- •§11. Критерий Коши сходимости числовой последовательности
3. Произведение .
1)
![]() ,
,![]()
![]() ,
,
2)
![]() ,
,![]()
![]() ,
,
3)
![]() ,
,![]() - неопределенность
вида
- неопределенность
вида
![]() .
.
Существуют еще другие виды неопределенностей, связанные со степенями.
Пример 3. Вычислить
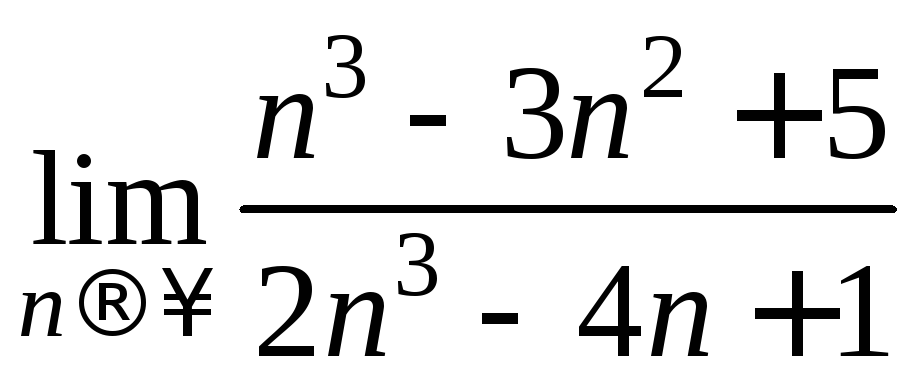
∆ Числитель
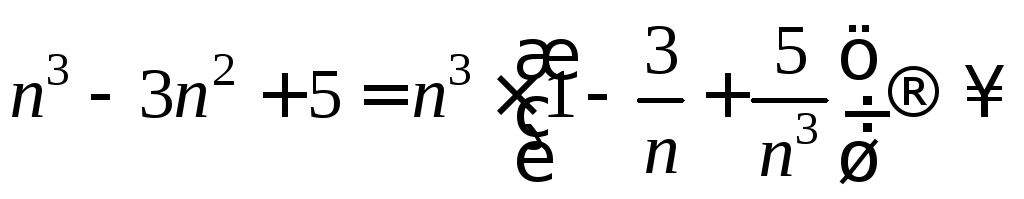 ,
,
Знаменатель
 ,
,
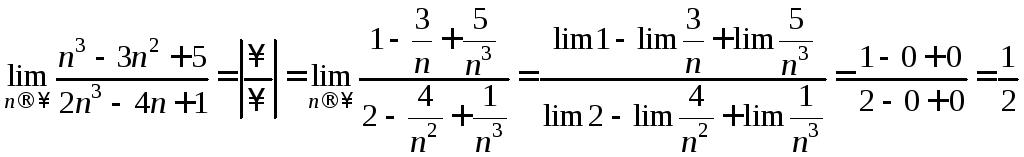 .∆
.∆
Пример 4. Вычислить
![]()
∆ Воспользуемся
формулой
![]() ,
тогда
,
тогда
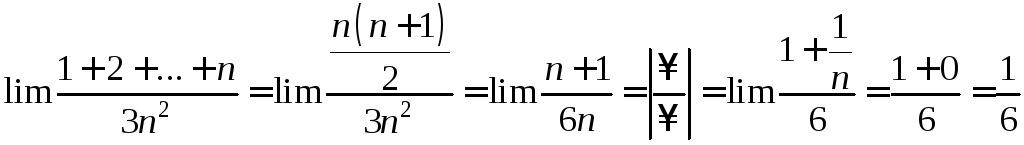 .
∆
.
∆
Пример 5. ∆
![]()
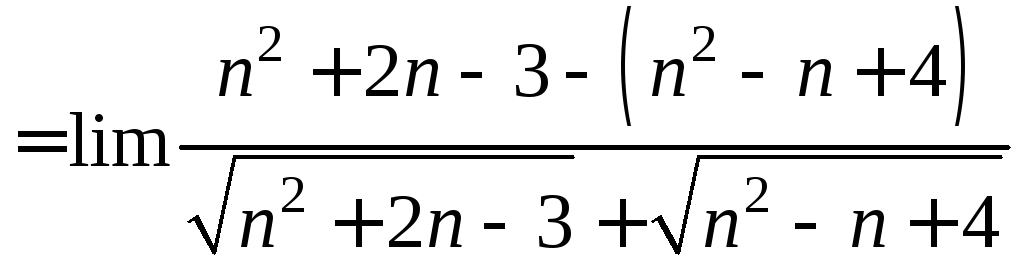
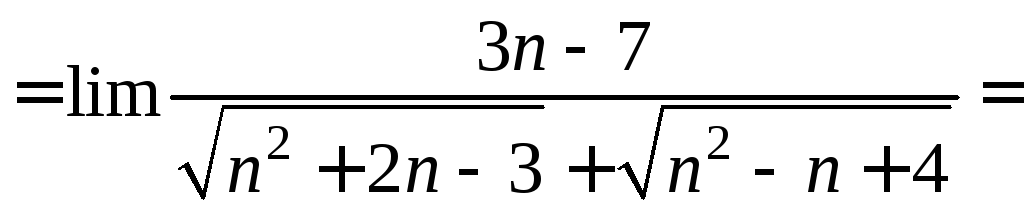
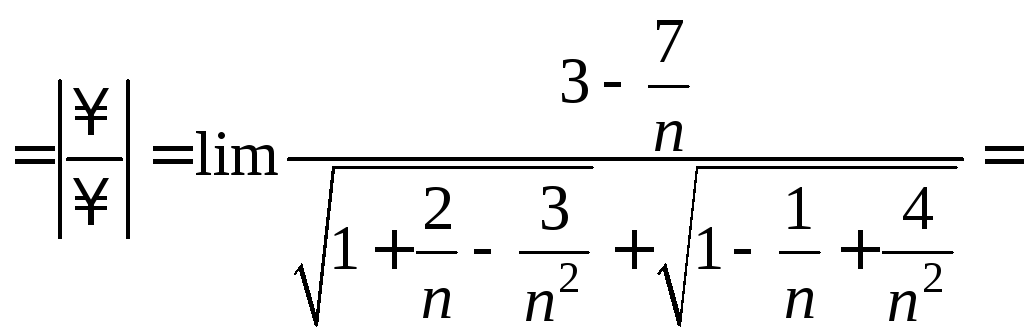
![]()
![]() .∆
.∆
Пример 6. Доказать,
что

∆ 1) Рассмотрим
случай a>1.
Покажем, что
![]()
![]() .
.
Выберем
![]() и найдем номер
и найдем номер![]() выполнено
выполнено![]() (так какa>1)
(так какa>1)
![]() .
.
Положим
![]() ,
тогда
,
тогда![]() выполнено
выполнено![]() верно
верно![]()
![]() приa>1.
приa>1.
2) Пусть 0<a<1.
Запишем
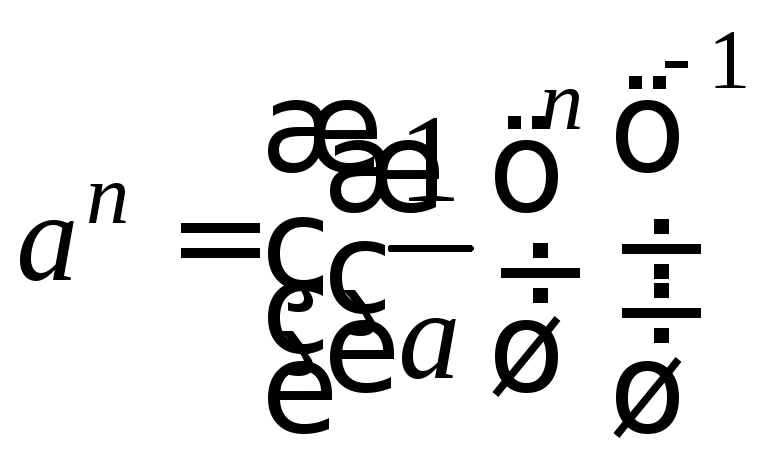 .
Так как 0<a<1,
то
.
Так как 0<a<1,
то
![]()
 - ББП (по п.1)
- ББП (по п.1)
 -
БМП
-
БМП![]() .
.
3) -1<a<0.
![]() (огр.БМП);
(огр.БМП);
4) a<-1.
Тогда
 .
Т. к.a<-1,
то
.
Т. к.a<-1,
то
![]() .
Т. к. в этом случае
.
Т. к. в этом случае![]() - БМП (см. п.3), то
- БМП (см. п.3), то - ББП и, следовательно,
- ББП и, следовательно,![]() .
.
5)
![]() .
.
6)
![]() .
.
7)
![]() не существует
(пример 3 §3).∆
не существует
(пример 3 §3).∆
Пример 7.
∆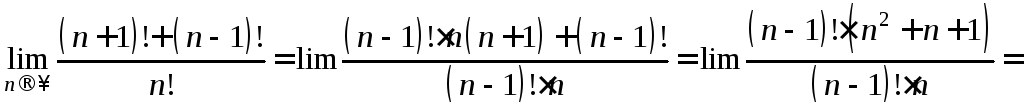
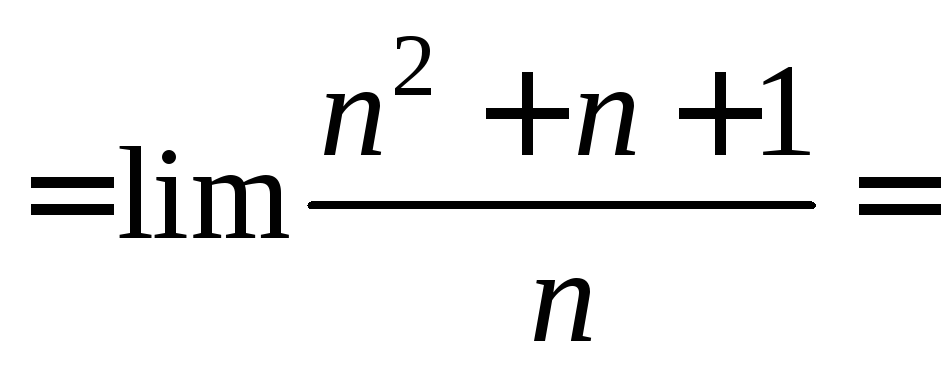
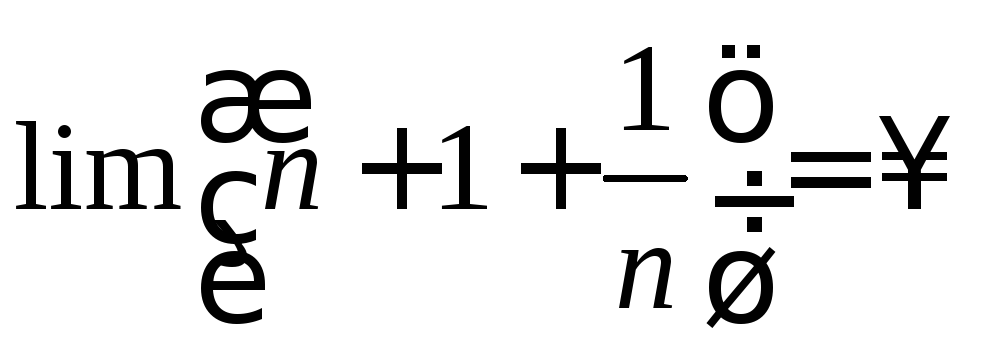 .∆
.∆
Пример 8.
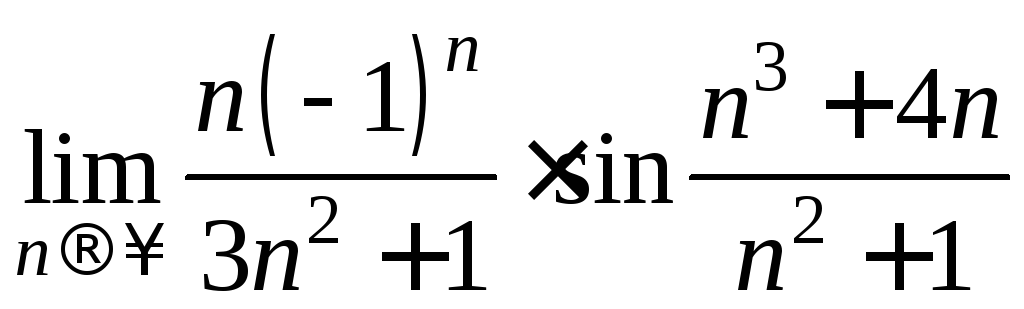 .
.
∆ Рассмотрим
последовательности
![]() ,
,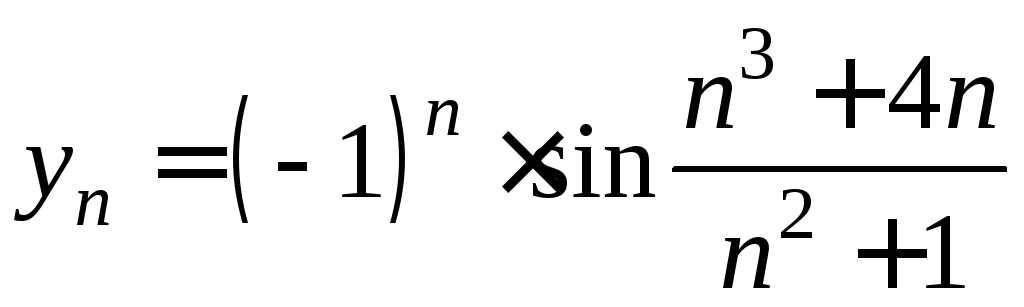 .
.
Надо найти
![]() .
.
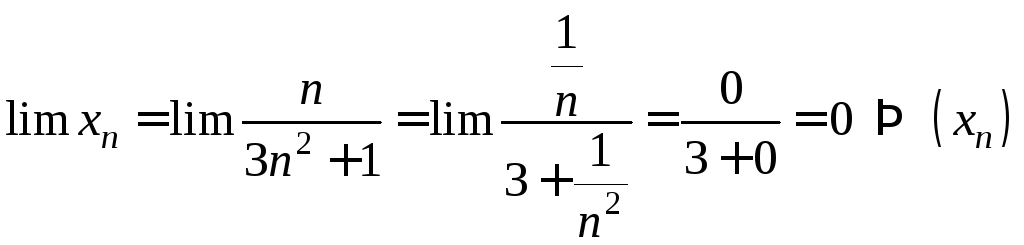 - БМП,
- БМП,
![]() - ограниченная
последовательность
- ограниченная
последовательность
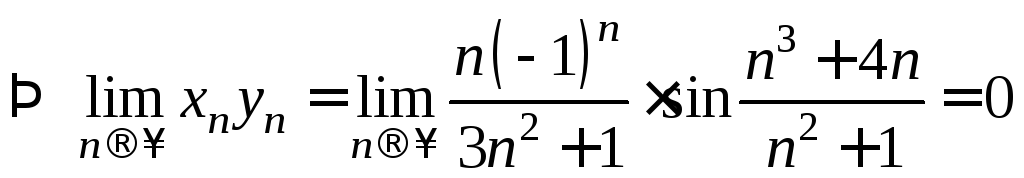 .∆
.∆
§7. Предел монотонной последовательности (признаки существования предела последовательности)
Определение 1.
Верхней
гранью
последовательности
![]() называется верхняя грань множества
значений элементов этой последовательности.
называется верхняя грань множества
значений элементов этой последовательности.
Обозначается
![]()
![]() .
.
Если множество
значений элементов последовательности
![]() ограничено сверху, то
ограничено сверху, то
![]() есть число:
есть число:
![]() Если множество значений неограниченно
сверху, то
Если множество значений неограниченно
сверху, то![]() .
.
Определение. 1.
![]() 1)
1)![]() ,
,
2) ![]() .
.
Определение 2.
Нижней
гранью
последовательности
![]() называется нижняя грань множества
значений этой последовательности.
называется нижняя грань множества
значений этой последовательности.
Обозначается inf xn.
Если множество
значений элементов последовательности
![]() ограничено снизу, то
ограничено снизу, то![]() .
Если множество значений не ограничено
снизу, то
.
Если множество значений не ограничено
снизу, то![]() .
.
Определение 2.
![]() 1)
1)![]() ,
,
2) ![]() .
.
Примеры.
1)
![]()
Множество значений
![]() .
.
2) ![]() ,
,
![]()
![]() ,
,
![]() .
.
Теорема 1. 1) Любая неубывающая, ограниченная сверху последовательность имеет конечный предел.
2) Любая невозрастающая, ограниченная снизу последовательность имеет конечный предел.
Доказательство.
![]() 1)
1)
![]() - ограниченная сверху
- ограниченная сверху![]() .
.
Докажем, что
![]() .
.
Выберем
![]() .
Тогда по определению 1' для этого
выполняется два условия:
.
Тогда по определению 1' для этого
выполняется два условия:
1) ![]() ,
,
2) ![]()
Так как
![]() - неубывающая, то
- неубывающая, то![]() .
.
Следовательно,
![]() выполнены условия 1) и 2), значит,
выполнены условия 1) и 2), значит,![]() выполнено
выполнено
![]() .
Т. е.
.
Т. е.![]()
![]()
![]() .
.
Итак,
![]()
![]() :
:![]() выполняется
выполняется
![]()
![]() .
.
Заметим, что из
условия 1) следует, что ![]() .
.
2) Доказывается аналогично.
Устанавливается,
что
![]() и, следовательно,
и, следовательно,![]() .
.![]()
Теорема 2. 1)
Всякая неубывающая, неограниченная
сверху последовательность
![]() имеет
имеет![]() .
.
2) Всякая
невозрастающая, неограниченная снизу
последовательность
![]() имеет
имеет![]() .
.
Доказательство.
![]() 1)
1) ![]() неограниченная сверху
неограниченная сверху![]() ,
,
![]() неубывающая
неубывающая![]() или
или![]()
![]() .
.
Т.о.
![]()
![]() .
.
2) Доказывается
аналогично, причем
![]() .
.
![]()
§ 8. Принцип вложенных отрезков
Пусть дана последовательность отрезков
![]() an<bn
an<bn
![]()
Определение 1. Последовательность отрезков называется последовательностью вложенных отрезков, если
![]() , (1)
, (1)
то есть каждый последующий отрезок содержится в предыдущем.
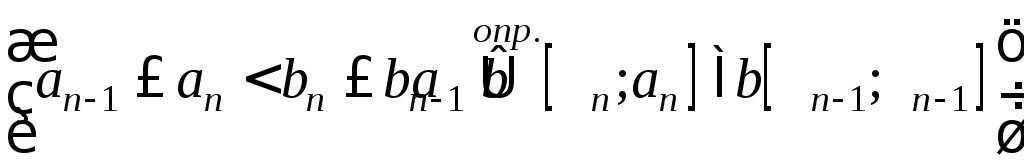
Определение 2.
Последовательность вложенных отрезков
называется стягивающейся,
если длины этих отрезков стремятся к
нулю при возрастании n,
то есть если
![]() .
.
Теорема. (принцип вложенных отрезков).
Для любой
стягивающейся последовательности
вложенных отрезков существует единственная
точка с,
принадлежащая всем отрезкам этой
последовательности, то есть такая, что
![]()
![]() .
.
Доказательство.
![]()
 Левые концы отрезков
последовательности (1) образуют неубывающую
последовательность:
Левые концы отрезков
последовательности (1) образуют неубывающую
последовательность:
![]() ,
а правые концы – невозрастающую
последовательность:
,
а правые концы – невозрастающую
последовательность:![]() Так как
Так как![]()
![]() ,
то
,
то
![]() – ограничена сверху; так как
– ограничена сверху; так как![]()
![]() то
то
![]() - ограничена снизу.
- ограничена снизу.
Так как
![]() - неубывающая и ограничена сверху, то
по теореме 1 § 7 она имеет предел:
- неубывающая и ограничена сверху, то
по теореме 1 § 7 она имеет предел:![]() ,
причем
,
причем
![]()
![]() . (2)
. (2)
По теореме 1 § 7
![]() ,
,![]()
![]() . (3)
. (3)
Тогда из соотношения
![]() .
.
Общее значение
и
обозначим через с.
Из (2), (3) следует, что
![]()
![]() ,
то есть точкас
принадлежит
всем отрезкам последовательности (1).
,
то есть точкас
принадлежит
всем отрезкам последовательности (1).
П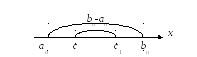 окажем,
чтос
единственная точка, принадлежащая всем
отрезкам последовательности (1). Допустим
противное. Пусть точка
с1с:
окажем,
чтос
единственная точка, принадлежащая всем
отрезкам последовательности (1). Допустим
противное. Пусть точка
с1с:
![]()
![]() .
Следовательно,
.
Следовательно,![]() должно выполняться неравенство
должно выполняться неравенство![]() ,
значит,
,
значит,![]() ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
![]()
Замечание.
Доказанная
теорема становится неверной, если в ней
вместо отрезков рассматривать интервалы.
Например, интервалы последовательности
вложенных интервалов (у
которой
![]() ):
):
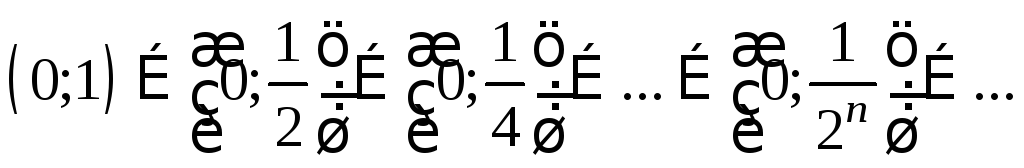
![]()
Интервалы этой
последовательности не имеют ни одной
общей точки, так как какую бы точку
![]() мы ни брали,
мы ни брали,![]() , и интервалы этой последовательности,
начиная с
, и интервалы этой последовательности,
начиная с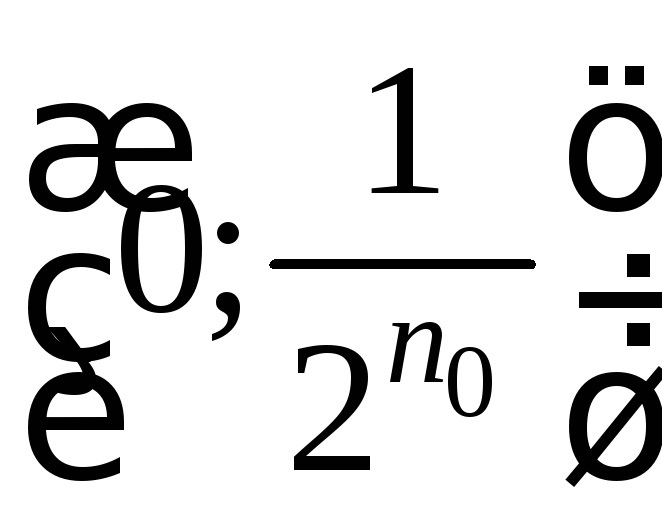 , не содержат т.
, не содержат т.![]() .
Точка 0 является общим левым началом
всех интервалов, но не принадлежит им.
.
Точка 0 является общим левым началом
всех интервалов, но не принадлежит им.
