
- •Введение в анализ
- •§1. Действительные числа
- •1. Понятие действительного числа
- •2. Модуль действительного числа и его свойства Определение. Модулем действительного числа а называется неотрицательное число, обозначаемое |а|, определяемое формулой:
- •Геометрический смысл: Пример 1.А);
- •По свойству 3
- •Число хнаходится от точкиана расстоянии меньшем, чемb.
- •3. Числовые множества. Промежутки. Окрестности
- •§ 2. Ограниченные и неограниченные множества. Верхние и нижние грани числовых множеств
- •§ 3. Предел последовательности
- •2. Предел последовательности. Пусть дана последовательность :(1)
- •3. Единственность предела
- •4. Ограниченность сходящейся последовательности
- •Доказательство.
- •5. Свойства сходящихся последовательностей
- •§ 4. Бесконечно малые последовательности
- •§ 5. Бесконечно большие последовательности (ббп)
- •§ 6. Свойства пределов, связанные с арифметическими операциями над сходящимися последовательностями
- •3. Произведение .
- •§7. Предел монотонной последовательности (признаки существования предела последовательности)
- •§ 8. Принцип вложенных отрезков
- •§ 9. Число е.
- •§10. Подпоследовательности
- •§11. Критерий Коши сходимости числовой последовательности
Введение в анализ
Логические символы:
![]() -
квантор общности;
-
квантор общности;
![]() х
– «для всех х»
(«для любого х»,
« для всякого х»);
х
– «для всех х»
(«для любого х»,
« для всякого х»);
![]() -
квантор существования;
-
квантор существования;
![]() х-
«существует х»;
х-
«существует х»;
![]() (
) – «не существует»;
(
) – «не существует»;
![]() - следствие
(из первого высказывания следует второе);
- следствие
(из первого высказывания следует второе);
![]() - равносильность
утверждений, стоящих по разные стороны
от знака
- равносильность
утверждений, стоящих по разные стороны
от знака
![]() ;
;
: ( | ) – « такой, что » («для которого»);
! – единственный.
§1. Действительные числа
1. Понятие действительного числа
Понятие числа
прошло длинный путь развития. Вначале
в связи с необходимостью подсчёта
предметов возникли простейшие числа -
натуральные
![]() ={1;2;3;4;…;n;…}.
На
={1;2;3;4;…;n;…}.
На
![]() действуют операции сложения и умножения,
то есть
действуют операции сложения и умножения,
то есть
![]() m,n
m,n![]()
![]() ,
m+n
,
m+n![]()
![]() и m
и m![]() n
n![]()
![]() .
.
Введение
вычитания привело к расширению множества
![]() до
до![]() – множествацелых чисел:
– множествацелых чисел:![]() ={0;±1;±2;±3;…}.
={0;±1;±2;±3;…}.
Введение деления
расширило множество целых чисел до
множества рациональных
чисел:
![]() =
=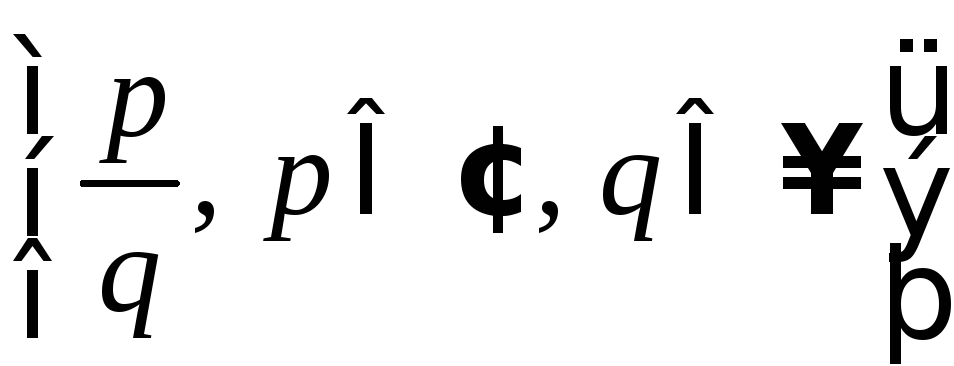 .
.
На множестве
![]() определены операции сложения, вычитания,
умножения, деления (кроме деления на
нуль).
определены операции сложения, вычитания,
умножения, деления (кроме деления на
нуль).![]()
![]() -
упорядоченное
множество, то есть
-
упорядоченное
множество, то есть
![]() a,b
a,b![]()
![]() либоa<b,
либо a>b.
либоa<b,
либо a>b.
![]() -
плотное
множество,
то есть
-
плотное
множество,
то есть
![]() a,b
a,b![]()
![]() :
a<b
:
a<b
![]() промежуточное рациональное числоc,
то есть
промежуточное рациональное числоc,
то есть
![]() c
c![]() :
a<c<b
(например:
:
a<c<b
(например:
![]() ).
).
Ясно, что
![]() a,b
a,b![]()
![]()
![]() бесконечно
много промежуточных рациональных чисел.
бесконечно
много промежуточных рациональных чисел.
![]() не является непрерывным множеством
(если отметить все рациональные числа
точками на числовой оси, то на ней будут
"дыры"- точки, которым не соответствует
никакое рациональное число).
не является непрерывным множеством
(если отметить все рациональные числа
точками на числовой оси, то на ней будут
"дыры"- точки, которым не соответствует
никакое рациональное число).
Необходимость
решать задачи, неразрешимые на множестве
![]() ,
привело к возникновению идеи "дополнения"
множества рациональных чисел. Например:
в
,
привело к возникновению идеи "дополнения"
множества рациональных чисел. Например:
в
![]() неразрешимо уравнение
неразрешимо уравнение
![]() .
То есть, нет такого рационального числа,
квадрат которого равен 2 Для доказательства
этого факта вначале введём определение.
Два рациональных числа
.
То есть, нет такого рационального числа,
квадрат которого равен 2 Для доказательства
этого факта вначале введём определение.
Два рациональных числа![]() и
и![]() называютсяравными,
если
называютсяравными,
если
![]() =
=![]() .
Поэтому каждое рациональное число можно
единственнымобразом
представить в виде несократимой дроби
.
Поэтому каждое рациональное число можно
единственнымобразом
представить в виде несократимой дроби
![]() ,
гдеp
и q
- взаимно простые.
,
гдеp
и q
- взаимно простые.
Утверждение.
![]() х
х
![]()
![]() :
:![]() .
.
Доказательство.
![]() Пусть
Пусть
![]()
![]()
![]() :
:![]() =
=![]() .
Пусть дробь
.
Пусть дробь![]() -
несократима (в противном случае её можно
сократить). Из равенства
-
несократима (в противном случае её можно
сократить). Из равенства![]() (1)
(1)![]()
![]() -
чётное, то есть
-
чётное, то есть![]() =
=![]() (2). Тогда (подставим (2) в (1)):
(2). Тогда (подставим (2) в (1)):![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() -
чётное
-
чётное![]()
![]() -
чётное. Получим, что
-
чётное. Получим, что![]() и
и![]() являются четными, то есть дробь
являются четными, то есть дробь![]() можно сократить. Полученное противоречие
доказывает, что наше допущение неверно
и не существует рационального числа,
квадрат которого равен
можно сократить. Полученное противоречие
доказывает, что наше допущение неверно
и не существует рационального числа,
квадрат которого равен![]() .
.![]()
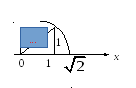 Число
Число
![]() является иррациональным. Изобразим на
числовой оси.
является иррациональным. Изобразим на
числовой оси.
Существуют
различные подходы к определению
иррационального числа. Один из них через
понятие бесконечной десятичной дроби.
Любое рациональное число представимо
в виде конечной или бесконечной
периодической десятичной дроби: (![]() =
=![]() ;
;![]() =
=![]() =
=![]()
![]() ).
Если число представимо в виде бесконечной
непериодической десятичной дроби, то
оно являетсяиррациональным:
(
).
Если число представимо в виде бесконечной
непериодической десятичной дроби, то
оно являетсяиррациональным:
(![]() =1,414213…;
=1,414213…;![]() =1,732050…;
π=3,141592…;
=1,732050…;
π=3,141592…;![]() =2,71828…).
=2,71828…).
Определение 1.
Множеством
действительных чисел называется
совокупность всех рациональных и
иррациональных чисел:
![]() (I- множество иррациональных чисел).
(I- множество иррациональных чисел).
Определение 2. Действительным числом называется любая бесконечная периодическая или непериодическая дробь.
Действительные
числа изображаются точками на числовой
прямой и заполняют всю прямую, без "дыр".
Множество
![]() непрерывно.
непрерывно.
Свойство
непрерывности R.
Пусть
![]() -
произвольные множества из
-
произвольные множества из![]() и
и![]() и
и ![]() выполняется
выполняется
![]() .
Тогда
.
Тогда![]()
![]() и
и ![]() выполняется
выполняется
![]() .
.
