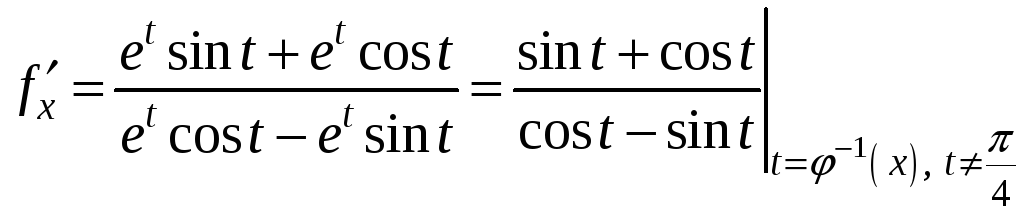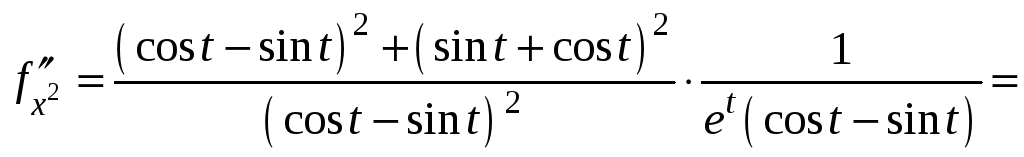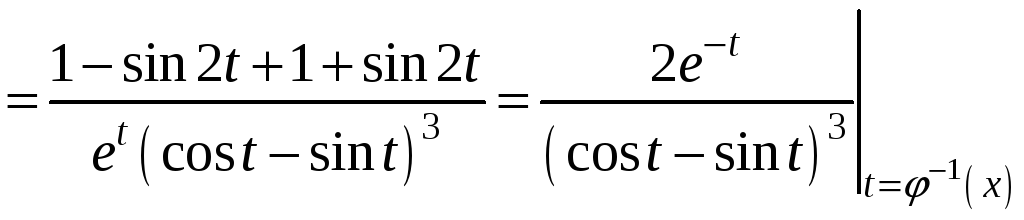Госы 5к Надя / лекции_1 / Кривые и функции

6

Кривые и функции, заданные параметрически

П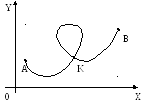усть точка движется по некоторой кривой АВ, то есть каждому моменту времени t соответствует определённая точка М(х;y) кривой АВ. Тогда

x=(t) - закон движения точки по оси ОХ,

y=(t) - закон движения точки по оси ОУ,

.

( и  должны быть дифференцируемы, т. к. существует скорость).

Уравнения (1)

полностью определяют кривую АВ. Переменная t (параметр), входящая в уравнения (1) может выражать не время, а другую физическую или геометрическую величину, то есть t – произвольный параметр.

Определение. Множество точек плоскости, координаты которых х и у удовлетворяют уравнениям (1), где  и  непрерывны на [α;β], называется кривой Жордана.

Уравнения (1) – параметрические уравнения кривой. Уравнения (1) задают не только совокупность точек, принадлежащих кривой, но и устанавливают порядок, в котором эти точки следуют друг за другом (при изменении t от α до β). При этом не исключено, что с одной и той же точкой (на рисунке точка К) движущаяся точка совместится дважды или более раз.

Точка M(x;y)=M((t);(t)) кривой Жордана называется кратной, если она соответствует более, чем одному значению параметра . Если кривая не имеет кратных точек (то есть разным значениям t соответствуют разные точки кривой), то она называется простой кривой.

Если при t=β уравнения (1) определяют ту же точку кривой, что и при t=α, то есть , то кривая (1) называется замкнутой.

Если замкнутая кривая не имеет кратных точек, кроме А=В, то она называется простой замкнутой кривой.

С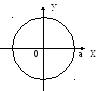истема (1) задаёт некоторую связь переменных х и у (какому-либо значению t соответствует определённое х и определённое у, значит, связь есть). Если из системы (1) удаётся исключить параметр t, то получаем уравнение кривой, связывающее координаты х и у.

Примеры.

1) x=acost,

y=asint, ,

- окружность с центром в точке (0;0) радиуса а.

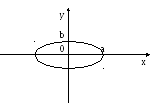
2) x=acost,

y=bsint, ,

- эллипс.

3) x=acost+x₀,

y=asint+y₀, ,

- окружность с центром в точке , радиуса а.

4) x=a(t-sint),

y=a(1-cost).

Пусть по прямой Ох катится окружность радиуса а.

Циклоида - линия, которую при этом описывает каждая точка окружности.

- первая арка циклоиды

При получим всю циклоиду.

5) ,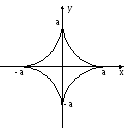

, - астроида (гипоциклоида)

t	0
х	1				0
y	0				1

Построим по точкам.

t
х	-1				0				1
y	0				-1				0

Из примеров видно, что кривая (1) не всегда является графиком некоторой функции, то есть уравнения (1) не всегда определяют функцию y=f(x) (хотя связывают х и у).

Пусть функция x=(t) имеет обратную , xX. Подставляя в функцию y=(t), получим , xX. Таким образом, если для функции x=(t)существует обратная функция, то система (1) определяет функцию y=f(x).

Определение. Задание функции y=f(x) с помощью системы (1) называется параметрическим заданием функции.

Если в параметрически заданной функции уравнение x=(t) разрешимо относительно t (t=t(x)), то параметрическое задание функции можно свести к явному: (но это не всегда можно сделать).

Пример. x=acost,

y=asint, ,

x=(t) монотонно убывает и непрерывна на , . Следовательно, существует обратная функция , определённая на . Значит, 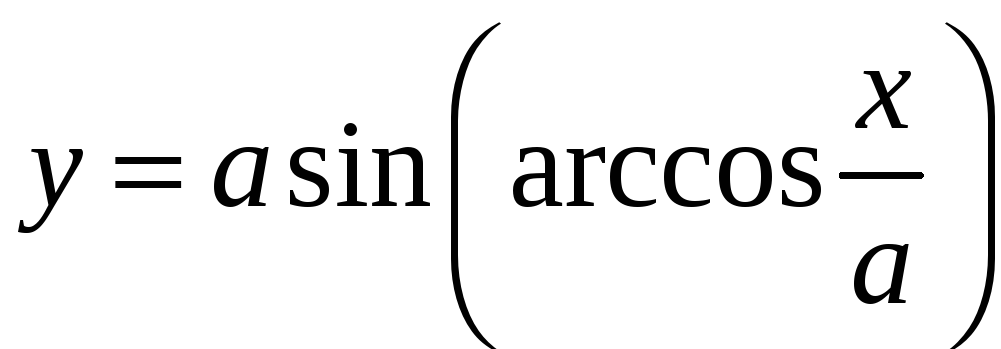- функция от х, определённая на .Так как , то y>0. Значит,

.

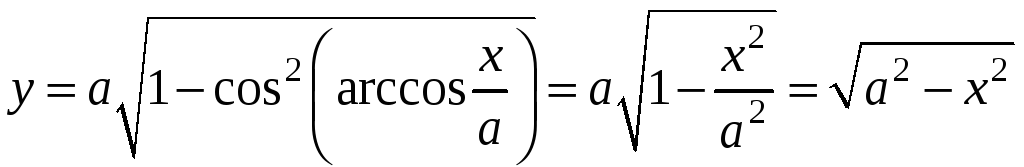Наоборот, всякую функцию y=f(x) можно многими способами представить параметрически в виде (1). Для этого достаточно задать совершенно произвольно функцию x=(t) параметра t. Тогда для y=f(x) становится функцией того же параметра: .

Примеры.

1) , .

Положим . Получаем

x=sint,

, .

2) y=f(x), .

x=t,

y=f(t), .

Таким образом параметрический способ задания функции является более общим.

Теорема 1. Если в системе (1) функции (t) и (t) непрерывны на и (t) на этом промежутке строго монотонна, то система (1) определяет непрерывную функцию y=f(x), определённую на .

Доказательство.

Так как (t) непрерывна на , то по следствию из II теоремы Больцано-Коши. . Так как x=(t) непрерывна и строго монотонна на , то она имеет обратную функцию , непрерывную и строго монотонную на . Тогда - композиция двух непрерывных функций на , следовательно, она является непрерывной на функцией.

Теорема 2. Пусть функция y=f(x) задана системой (1). Если функции  и  непрерывно дифференцируемы на , и на этом отрезке , то функция f дифференцируема на некотором промежутке D и справедлива формула

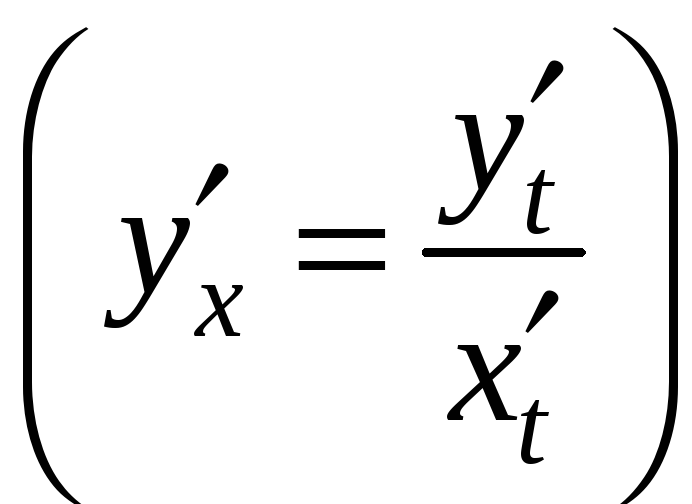(2)

Доказательство.

Так как непрерывна и на , то одного знака на (I теорема Больцано–Коши). Следовательно (это будет доказано позже), (t) строго монотонна на . Значит, существует обратная функция , xD. Так как , то обратная функция дифференцируема .

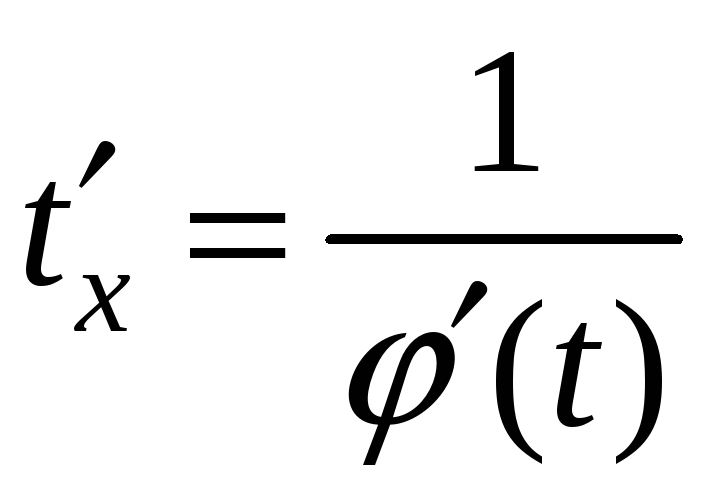Так как y=(t), а , то - сложная функция. Она дифференцируема на D, так как  и  дифференцируемые функции, и её производная: .

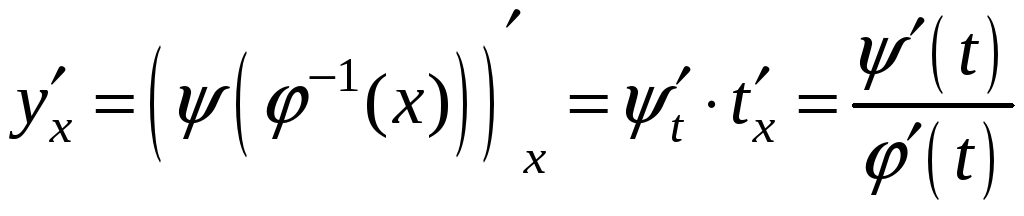Пример. x=acost

y=asint, ,

 (t)=acost, непрерывна на , на ,

(t)=asint, , , , . 

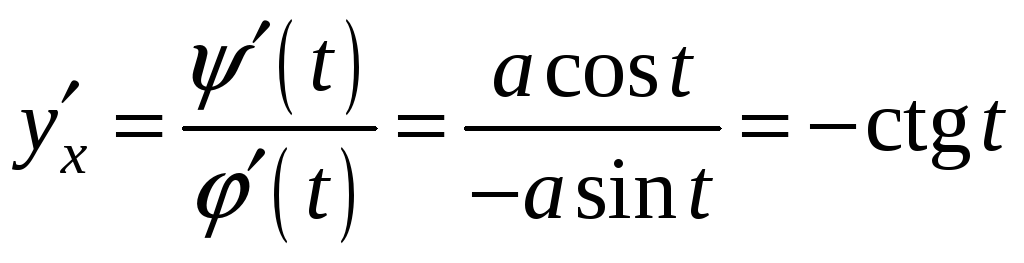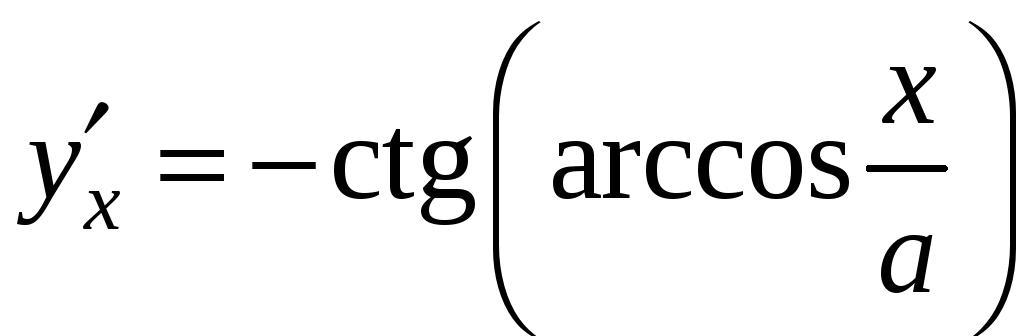Замечание 1. Если , , то .

Если , то в этой точке не определена (хотя это не значит, что не существует).

Например, рассмотрим функцию , , .

Пусть , .

, .

Точке t=0 соответствует точка х=1.

, , не определена.

Если функции (t), дважды дифференцируемы и , то существует :

.

Пример 1.

(*)

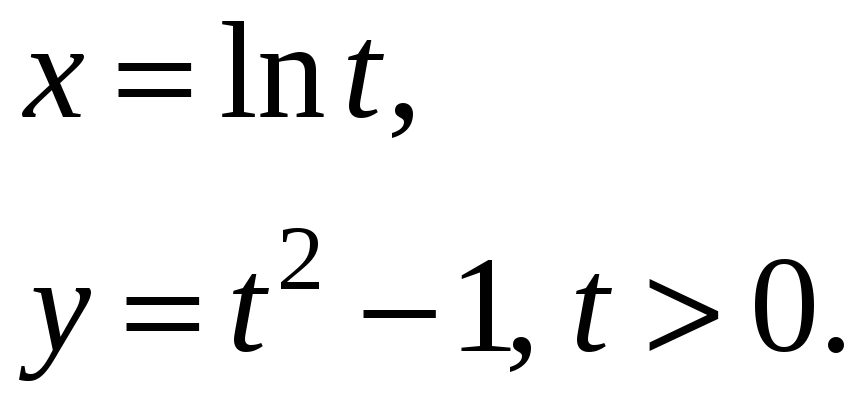x=(t)=lnt - непрерывная, строго монотонная при t>0 существует обратная функция , . Тогда уравнения (*) задают на функцию y=f(x). Найдём .

I способ: , , ,

, ,

, ,

.

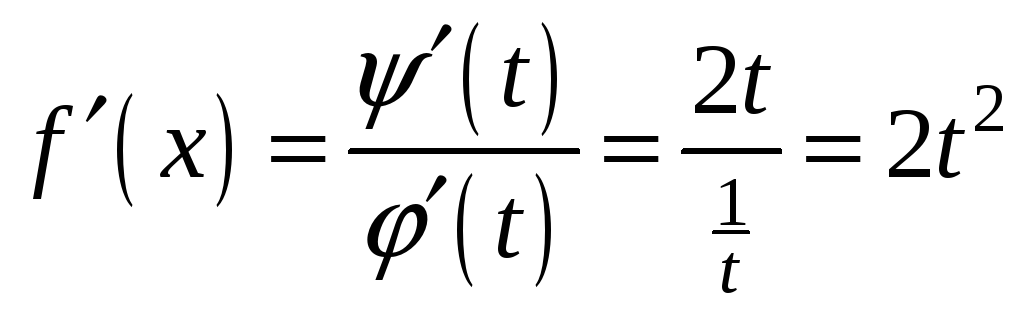II способ:

, (но не всегда выражаются через х).

Пример 2.

, .

На некотором промежутке эти формулы задают функцию y=f(x).