§23. Свойства непрерывных функций
1. Свойства функций, непрерывных в точке
Теорема 1. Если функция f(x) непрерывна в точке x0, то она ограничена в некоторой окрестности V(x0) этой точки.
Доказательство.
Т.к.
f(x)
непрерывна в точке x0,
то согласно определению существует
.
Следовательно, по теореме о том, что
функция, имеющая предел в точке, ограничена
в некоторой окрестности этой точки,
получаем, что f(x)
ограничена в V(x0).
Теорема
2. Если функция
f(x)
непрерывна в точке x0
и
(
),
то
.
Доказательство.
Проведем
доказательство для
.
f(x)
непрерывна в точке x0,
значит, по определению
.
Тогда по определению предела функции
в точке для числа 
>0
выполнено
.
Тогда
.
Прибавим ко всем частям неравенства
,
получим:
xV(x0,
).
Случай
доказывается аналогично.
2. Свойства функций, непрерывных на промежутке
Теорема 3. (первая теорема Больцано-Коши). Пусть f(x) непрерывна на [a;b] и на концах этого отрезка принимает значения разных знаков, тогда существует точка c(a;b), такая, что f(c)=0.
Доказательство.
Пусть
для определенности f(a)<0,
f(b)>0,
разделим отрезок [a;b]
пополам точкой
.
Еслиf(c1)=0,
то теорема доказана и c=c1.
Пусть f(c1)0. Если f(c1)<0, то на концах отрезка [c1;b] f(x) имеет значение разных знаков. Если f(c1)>0, то на концах отрезка [a;c1] функция имеет значение разных знаков. Обозначим через [a1;b1] ту половину [a;b], на концах которой функция принимает значения разных знаков f(a1)<0, f(b1)>0.
Разделим
[a1;b1]
пополам точкой
.
Еслиf(c2)=0,
то c=c2
и теорема доказана. Если f(c2)0,
то положим
или
в зависимости от того, на каком из
отрезков функция принимает значения
разных знаков. Получимf(a2)<0,
f(b2)>0.
Продолжим процесс деления далее. Возможны
два случая:
После конечного числа шагов получим точку
.
Тогда
и теорема доказана.В любой точке деления
.
В этом случае процесс деления продолжается
бесконечно. В результате получим
последовательность отрезков [a1;b1],
[a2;b2],
…[an;bn]…,
которая является последовательностью
вложенных отрезков.
.
Длина n-го
отрезка
.
Следовательно, по теореме о вложенных
отрезках существует точка с
принадлежащая всем отрезкам этой
последовательности, при этом
.
Так
как по условию
,
тоf(x)
непрерывна в точке c[a;b].
По определению по Гейне это означает:
, 
.
Так
как
.
Теорема
4 (вторая
теорема Больцано-Коши). Пусть
и на концах [a;b]
принимает различные значения f(a)=A,
f(b)=B,
AB.
Тогда, каково бы ни было число
: A<<B,
на (a;b)
найдется точка с:
f(c)=.
Доказательство.
Пусть
A<B.
Возьмем
: A<<B.
Рассмотрим вспомогательную функцию
на [a;b],
она непрерывна на [a;b]
как разность двух непрерывных функций.
.
Значит,
для
на [a;b]
выполняется условие первой теоремы
Больцано-Коши. Следовательно,
.
.
Данная теорема утверждает, что любое число, промежуточное между двумя значениями непрерывной функции, также является значением этой функции.
Первая теорема Больцано - Коши является частным случаем второй (с=0).
Следствие. Если функция f(x), заданная на некотором промежутке D, непрерывна на D, то совокупность ее значений f(D) также представляет собой некоторый промежуток.
Доказательство.
Обозначим
(m
и M
могут быть числами или
).
Тогда вf(D)
не может быть y:
y<m
и y>M.
Покажем что
.
Выберем
.
По определению нижней грани
,
по определению верхней грани
.
Получим
,
то есть
.
Тогда по второй теореме Б.-К.
.
Mы
получили, что
.
Концы
промежутка (m;M)
могут как принадлежать, так и не
принадлежать f(D),
т.е. f(D)
может быть интервалом (m;M),
полуинтервалом [m;M),
(m;M]
или отрезком [m;M],
т.е.
Теорема 5 (первая теорема Вейерштрасса). Если f(x) непрерывна на [a;b], то f(x) ограничена на [a;b].
Доказательство.
Предположим
противное, что f(x)
не ограничена на [a;b].
Пусть вначале f(x)
не ограничена сверху на [a;b].
Это значит, что
.
M=1
,
M=2
,
…………………….
M=n
,
……………………..
В
результате получим последовательность
(xn):
,
т.е.
.
Следовательно, (xn)
ограничена, а
.
По
теореме Больцано - Вейерштрасса из
ограниченной последовательности (xn)
можно выделить сходящуюся
подпоследовательность
,
.
В точке с
функция непрерывна, следовательно,
- конечное число. С другой стороны,
.
Полученное противоречие доказывает,
что предположение неверно, значит,f(x)
ограничена сверху на [a;b].
Аналогично
доказывается, что f(x)
ограничена снизу на [a;b].
Следовательно, f(x)
ограничена на [a;b].
Замечание. Теорема 5 справедлива только для отрезка.
Пример.
,
но не ограничена на нем:
.
Действительно,
.
1)
,
возьмем
;
2)
,
возьмемх-
любое из интервала(0;1),
.
Пусть f(x) определена на множестве E.
Определение.
Функция f(x)
имеет в точке
x0
наибольшее
(наименьшее)
значение на
множестве
E,
если xE
выполнено
.
Е
слиf(x)
имеет на E
наибольшее значение M,
то
;
еслиf(x)
имеет на E
наименьшее значение m,
то
.
Обратное не всегда верно:f(x)
может иметь верхнюю (нижнюю) грань, но
не иметь наибольшего (наименьшего)
значения.
Пример.
.
,
но наибольшего и наименьшего значений нет.
Теорема 6 (вторая теорема Вейерштрасса). Если функция f(x) непрерывна на [a;b], то на этом отрезке она достигает своих нижней и верхней граней (или имеет наибольшее и наименьшее значения).
Доказательство.
Так
как
,
тоf(x)
ограничена на [a;b]
(по первой теореме Вейерштрасса).
Следовательно,
,
и х[a;b]
.
Покажем,
что f(x)
достигает наибольшего значения M
на [a;b],
т.е.
.
От противного. Пусть
.
Рассмотрим вспомогательную функцию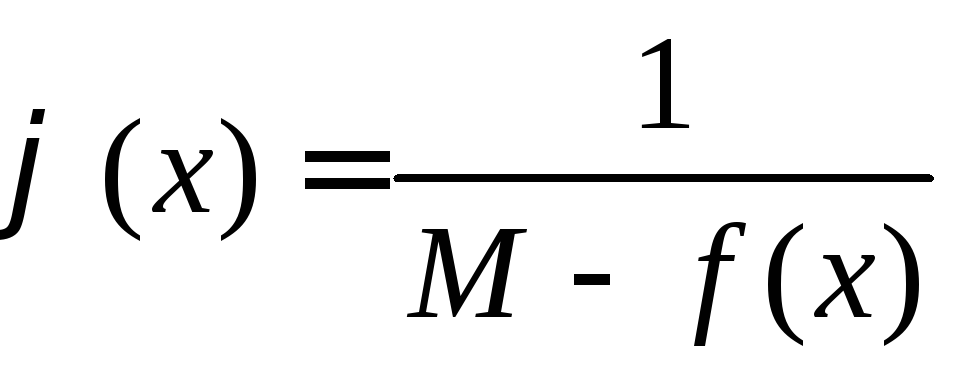
,
непрерывную как частное двух непрерывных
функций (M-f(x)0,
т. к. f(x)<M).
Следовательно, по первой теореме
Вейерштрасса (х)
ограничена на [a;b].
Значит,
:х[a;b]
.
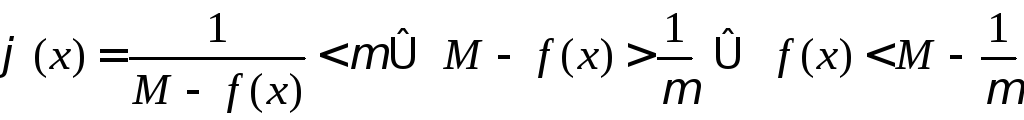Получили,
что число
является верхней границей дляf(x),
но это противоречит тому, что M
– наименьшая верхняя граница функции
f(x)
(по определению sup).
Таким образом, предположение неверно
и, значит,
.
Аналогично
доказывается, что
.
Т.е. непрерывная на отрезке функция
имеет наибольшее и наименьшее значения.
Замечание. Для интервалов и полуинтервалов вторая теорема Вейерштрасса не выполняется.
Например,
,
но не имеет ни наибольшего, ни наименьшего
значения.
Следствие
1. Если
,
то множеством ее значений будет [m;M],
где
.
Следствие
2. 1) Если
f(x)
непрерывна и возрастает на [a;b],
то множеством ее значений будет
.
2)
Если f(x)
непрерывна и убывает на [a;b],
то множество ее значений будет
.