§ 21. Непрерывность функции

1. Основные определения.

Пусть функция f(x) определена в окрестности точки x₀ V(x₀), x₀.

Определение 1. Функция f(x) называется непрерывной в точке x₀, если она в этой точке имеет предел, равный значению функции в этой точке, т.е. если

. (1)

Определение 2. (по Гейне) Функция f(x) называется непрерывной в точке х₀, если ,выполнено.

Определение 3. (по Коши) f(x) называется непрерывной в точке х₀, если выполнено.

Определение 4. (в терминах окрестностей) Функция f(x) называется непрерывной в точке х₀, если выполнено.

Равенство (1)  . (2).

Обозначим - приращение аргумента в точкех₀, - соответствующее приращение функции в точкех₀. Если , то. Значит, (2) .

Следовательно, получим эквивалентное определение.

Определение 5. Функция f(x) непрерывна в точке x₀, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, т.е. .

Определение 6. Если функция f(x) не является непрерывной в точке x₀, (т.е. если не выполняется условие (1)), то она называется разрывной в точке x₀, а точка x₀ называется точкой разрыва функции f(x).

Точку x₀, в которой функция не определена, но определена в , также будем называть точкой разрыва, хотя в ней равенство (1) вообще не определено (нет правой части).

Пример. непрерывна в любой точке.

 Придадим значению аргумента x₀ приращение , получим точку. Тогда функция получит приращение

;

.

Следовательно, непрерывна в любой точке.

Определение 7. Функция f(x) называется непрерывной слева (справа) в точке x₀, если ().

Теорема 1. Для того, чтобы функция f(x) была непрерывна в точке x₀ необходимо и достаточно, чтобы она была непрерывна в этой точке слева и справа.

Доказательство следует из определения непрерывности и теоремы об односторонних пределах (доказать самостоятельно).

Определение 8. Функция f(x)называется непрерывной на множестве Е, если она непрерывна в каждой точке этого множества.

Если Е=[a;b], то функция непрерывна на [a;b], если она непрерывна на (a;b), а в точке а непрерывна справа и в точке b непрерывна слева.

Множество всех точек, непрерывных на отрезке [a;b], обозначается С[a;b].

Например, - значитнепрерывна на [a;b]

Например, непрерывна на(см. пример).

2.Непрерывность суммы, разности, произведения и частного

Теорема 2. Если функции f(x) и g(x), непрерывны в точке x₀, то 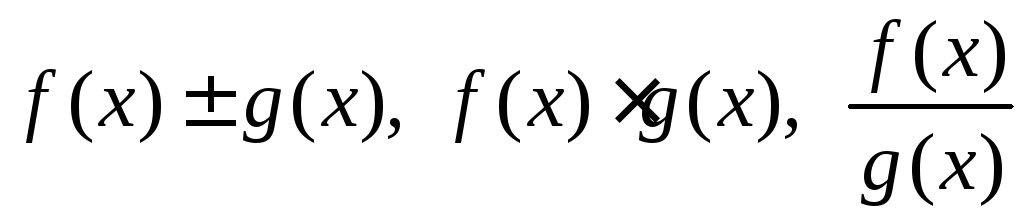(если) непрерывны в точкеx₀.

Доказательство.

Доказательство следует из теоремы арифметических операциях над пределами и определения непрерывности. Докажем для .

Так как инепрерывны в точкеx₀, то по определению 1 и. Тогда по теореме о пределе суммы=.

Следовательно, функция непрерывна в точкеx₀.

Следствие. Если функции f(x) и g(x), непрерывны на D=<a;b>, то на D непрерывны функци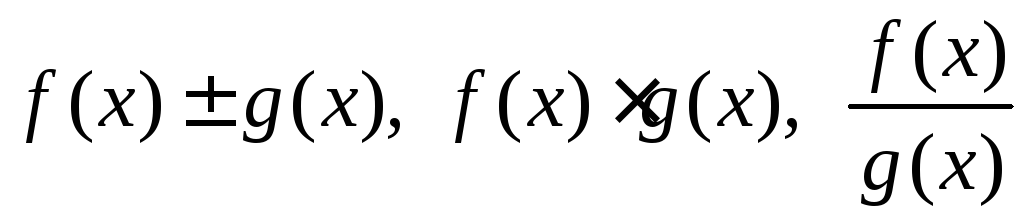и (еслинаD).

3. Непрерывность некоторых основных элементарных функций

1. .

 . Значит, непрерывна на.

2. .

 . Значит, f(x)=x непрерывна на .

3. .

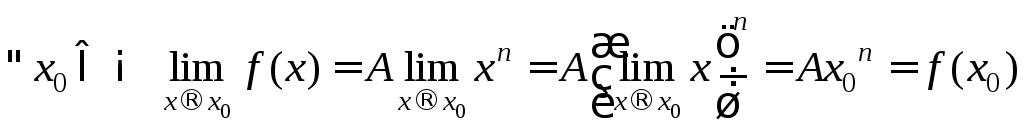 . Следовательно, непрерывна на.

4. .

(из п.3 и т.2). Значит, непрерывна на.

5. 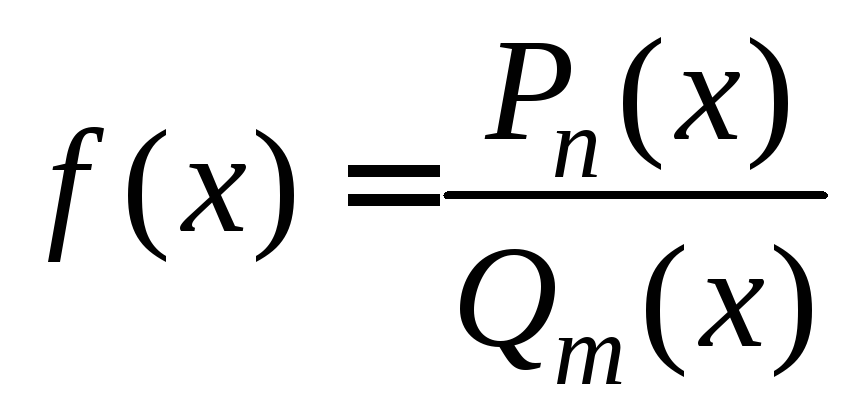-непрерывна , кроме точек, в которых, как частное непрерывных функций.

6. .

 Придадим произвольной точке приращение , получим точку, тогда функция получит приращение:

.

Надо показать, что , т. е.>0 >0: x: |x|<  |f(x₀)|<

 . (*)

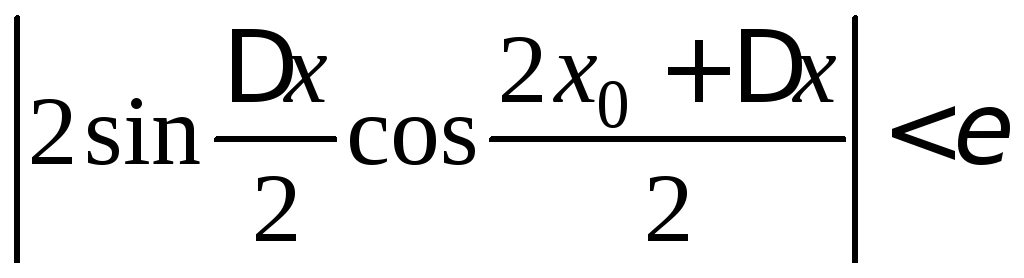Т. к. 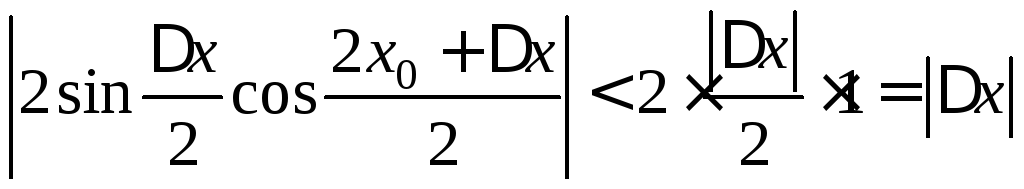, то если |x|<, значит выполнено и неравенство (*). Поэтому надо взять .

Значит, непрерывнанепрерывна на.

7. непрерывна на (доказательство аналогично).

8. 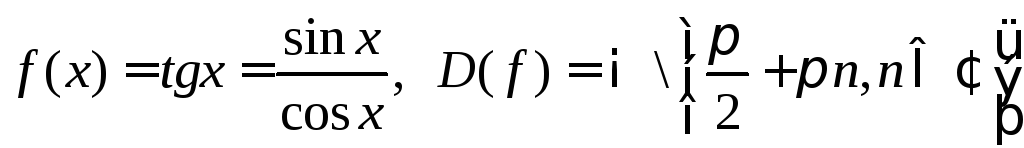непрерывна как частное двух непрерывных функций.

9. непрерывна как частное двух непрерывных функций.

10. ,D(f )=.

 Пусть . Рассмотрим случайa>1 (0<a<1 - аналогично)

1) Докажем, что функция непрерывна в точке x₀ справа, т.е. .

Выберем >0. Найдем >0: x: x₀<x<x₀+  0<x- x₀< выполнено неравенство (3)

.

Т.к. , то, следовательно, неравенство (3) равносильно

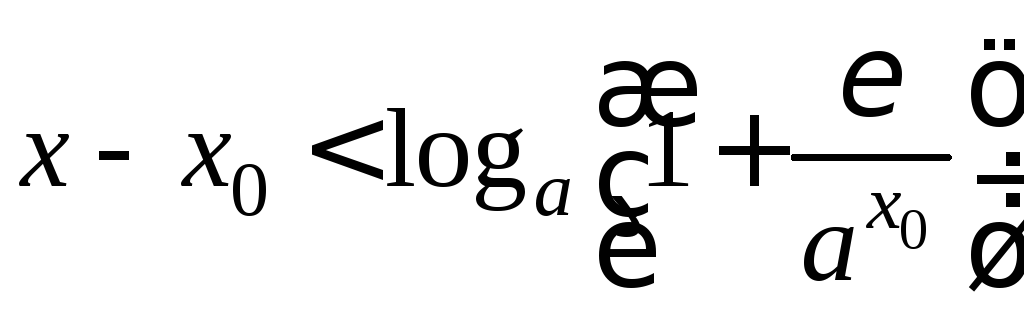. (4)

Положим 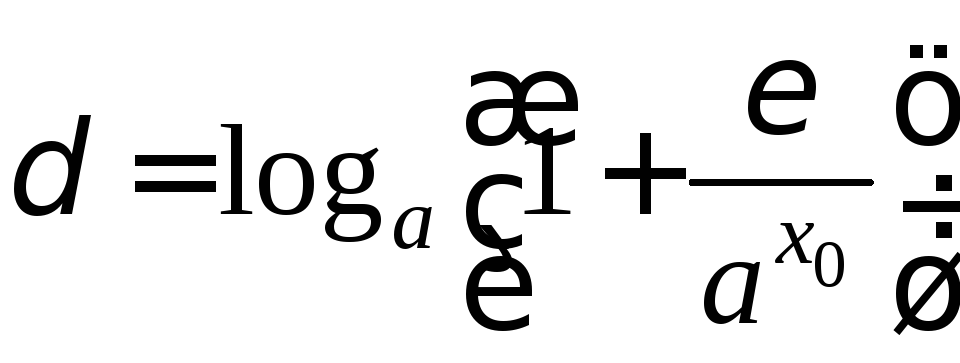. Тогда для всехх, удовлетворяющих неравенству x- x₀< выполнено неравенство (4), а, значит, и неравенство (3). Следовательно, .

2) Докажем что функция непрерывна в точке x₀ слева, т. е. .

Выберем >0. Найдем >0: x: x₀ -<x<x₀  -<x- x₀<0 выполнено неравенство (3).

Т.к. , то EMBED Equation.DSMT4

EMBED Equation.DSMT4 .

Значит, неравенство (3) равносильно EMBED Equation.DSMT4EMBED Equation.DSMT4

. (5)

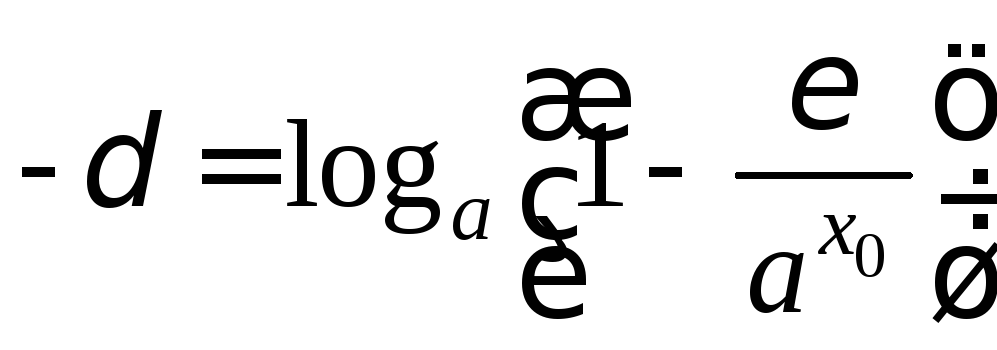
Возьмем 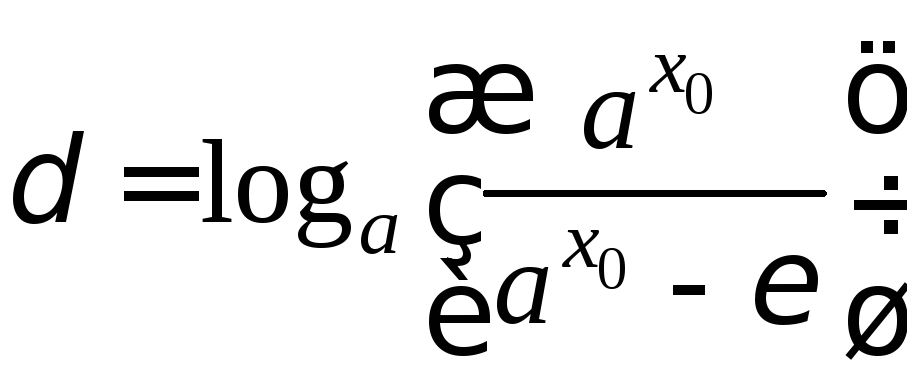 . Тогда для всехх, удовлетворяющих неравенству x- x₀>- выполнено неравенство (5), а, значит, и неравенство (3). Следовательно, .

Из 1), 2) следует что функция f(x)=a^x непрерывна в точке x₀, т. е. . Т. к.x₀  – произвольная точка, то показательная функция непрерывна на . 

11. (a>0, a1), D(f)=(0;+), непрерывна как функция, обратная к показательной ( теорема будет доказана позже).