
РГР по Физике
.pdf
Задача 13. Магнитная индукция В на оси тороида без сердечника (внешний диаметр 60 см, внутренний - 40 см) содержащего 200 витков, составляет 0,16 мТл. Определите силу тока в обмотке тороида.
Дано:
d1 = 60 см = 0,60 м; d2= 40 см = 0,40 м; N = 200;
B = 0,16 мТл = 0,16·10 -3 Тл.
Найти: I = ?
Циркуляция вектора В равна:
R |
= ∫ Bl dl = μ0 |
∑ Ik , |
|
∫ Bdl |
(1) |
||
L |
L |
k |
|
т.е. пропорциональна алгебраической сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция, μ0 - магнитная постоянная. В качестве контура выберем окружность, расположенную так же как и линия магнитной индукции, т.е. окружность некоторыми радиусом r, центр которой расположен на оси тороида. Из условия симметрии следует, что модуль вектора магнитной индукции во всех точках линии магнитной индукции одинаков, а поэтому выражение (1) можно записать в виде:
R R |
2π ×r |
|
∫ Bdl |
= B ∫ dl = 2π × rB = μ0 NI , |
(2) |
L |
0 |
|
(учли, что сила тока во всех витках одинакова, а контур охватывает число токов, равное числу витков тороида). Средняя линия тороида равна:
r = |
(d1 + d2 ) |
. |
(3) |
|
|
||||
|
4 |
|
|
|
Подставив (3) в (2) находим искомую силу тока: |
||||
I = |
π (d1 + d2 )B |
. |
||
|
2μ0 N |
|||
|
|
|
||
После подстановки числовых значений имеем:
I = |
π × (0,60 + 0,40) × 0,16 ×10 |
-3 |
|
2 |
× 4π ×10-7 200 |
= 1A. |
|
|
|
||
Ответ: I = 1A.
41

Задача 14. Протон, пройдя ускоряющую разность потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 0,2 Тл и начал двигаться по окружности. Вычислить радиус окружности.
Дано:
U = 400 В; В = 0,2 Тл;
е = 1,60×10-19 Кл; m = 1,67×10-27 кг;
α = π / 2, sin α = 1;
Найти: R = ?
Решение: На заряженную частицу, влетевшую в магнитное поле, действует сила Fл, называемая силой Лоренца. Она вычисляется по формуле
FЛ = evB sin α,
где е - заряд частицы; v - ее скорость; В - индукция магнитного поля, в котором движется частица; α - угол между направлением векторов скорости и индукции. Поскольку по условию задачи протон движется по замкнутой траектории (окружности), можно заключить, что составляющая вектора скорости в направлении вектора В равна нулю, т. е. α = 90°.
Направление силы Лоренца подчиняется, как известно, пра-
вилу левой руки. Угол между направлениями v и Fл всегда состав-
ляет 900. Следовательно, сила Лоренца является центростремительной силой, т. е. Fл = Fцс или
evB sin α = mv2 , R
где |
m - масса протона; R - радиус окружности, по которой дви- |
|||
жется протон. |
|
|
|
|
|
Отсюда |
|
|
|
|
R = |
mv |
|
|
|
|
. |
(1) |
|
|
eB sin α |
|||
Протон получил скорость, пройдя ускоряющую разность потенциалов. По закону сохранения энергии работа A , совершенная полем при перемещении протона, равна кинетической энергии T, приобретенной протоном, т. е.
А = Т. |
(2) |
42

Работа сил электрического поля при перемещении протона определяется по формуле
A = e U . |
(3) |
||
Кинетическая энергия протона |
|
||
T = |
mv2 |
. |
(4) |
|
|||
2 |
|
|
|
Подставив выражение А по (3) и выражение Т по (4) в (2), получим
eU = |
mv2 |
, откудаv = |
2eU |
. |
(5) |
|
|
||||
2 |
|
m |
|
||
Подставляя выражение для v в (1), получим
R= 
 2emU = 1,45 ×10−2 м. eB sin α
2emU = 1,45 ×10−2 м. eB sin α
Ответ: R = 1,45 ×10−2 м.
Задача 15. Плоская рамка площадью S = 100 см2, содержащая N = 20 витков тонкого провода, вращается в однородном магнитном поле с индукцией В = 100 мТл. Амплитуда э. д. с. индукции Emax = 10 В. Определить частоту вращения рамки.
Дано:
S = 100 см2 = 100 ·10 -4 м2; N = 20
В = 100 мТл=100 ·10 -3 Тл;
Emax = 10 В;
Найти: n =?
Решение: Для определения частоты вращения рамки исполь-
зуем понятие угловой скорости вращения:
ω = 2π = 2πn,
T
где Т - период вращения; n - частота вращения. Отсюда
n = |
ω |
(1) |
|
2π . |
|||
|
|
|
|
Угловую скорость вращения найдем из выражения для ЭДС индукции, возникающей в рамке при вращении его в магнитном поле:
E = NBSω sin ωt, |
(2) |
43

где |
Е — мгновенное значение э. д. с. индукции. |
|
||||
|
Амплитудой Е является значение E0, соответствующее значе- |
|||||
нию sinωt = l. |
|
|
|
|
|
|
|
Из соотношения (2) имеем |
|
|
|
||
|
|
ω = |
|
E0 |
. |
(3) |
|
|
|
|
|||
|
|
|
|
NBS |
|
|
|
Подставив выражение ω по (3) в (1), получаем |
|
||||
|
n = |
E0 |
= 79,5с−1 . |
|
||
|
|
|
|
|||
|
2πNBS |
|
|
|
||
Ответ: n = 79,5с−1.
Задача 16. В цепь переменного тока с действующим значением напряжения U = 220 В и частотой ν = 50 Гц последовательно включены резистор с активным сопротивлением R = 5 Ом и катушка индуктивности. Определите индуктивность L катушки, если амплитудное значение I0 сила тока в цепи равно 2 А.
Дано:
U = 220 В; ν = 50 Гц; R = 5 Ом; I0 = 2 А.
Найти:L = ?
Решение: Индуктивность катушки можно найти из формулы полного сопротивления заданной в задаче цепи переменного тока:
|
|
|
|
|
|
|
Z = R2 + (ωL)2 = R2 + (2πνL)2 , |
(1) |
|||||
(учли, что циклическая частота ω = 2πν). |
|
|||||
Согласно закону Ома, |
|
|||||
|
Z = |
U 0 |
, |
(2) |
||
|
|
|||||
|
|
I0 |
|
|||
где амплитудное значение U0 напряжения связано с действующим значением U напряжения соотношением
U = |
U |
0 |
|
. |
(3) |
|
|
|
|||
|
 2
2
Подставив выражения (1) и (3) в формулу (2), получим
44

R2 + (2πνL)2 = 
 2U ,
2U ,
I0
откуда искомая индуктивность катушки
|
1 |
|
2U 2 |
||
L = |
|
|
|
|
− R2 = 0,495Гн . |
2πν |
|
I 2 |
0 |
||
|
|
|
|||
Ответ: L = 0,495Гн.
Задача 17. Колебательный контур состоит из плоского воздушного конденсатора с двумя пластинами площадью по S=100 см2 каждая и катушки с индуктивностью L = 10-5 Гн. Период колебаний в контуре T = 10-7с. Определить расстояние между пластинами конденсатора.
Дано:
S= 100 см2= 100·10-4 м2;
L= 10-5 Гн;
T= 10-7 с.
Найти: d = ?
Решение: Искомое расстояние может быть найдено из фор-
мулы емкости плоского конденсатора
C = ε0εS , d
где ε0 – электрическая постоянная; ε - диэлектрическая проницаемость среды между пластинами конденсатора; S – площадь пластины конденсатора; d – расстояние между пластинами.
Отсюда
d = |
ε |
0εS |
(1) |
|
. |
C
Емкость конденсатора С найдем из формулы Томсона, определяющей период колебаний Т в колебательном контуре,
T = 2π 
 LC , где L — индуктивность катушки. Отсюда
LC , где L — индуктивность катушки. Отсюда
C = |
T 2 |
|
|
. |
|
4π 2 L |
||
Подставив это выражение С в (1), получим
45

d = |
4π 2ε 0 × ε × S × L |
= 3,49 ×10-3 |
м. |
(2) |
|
||||
|
T 2 |
|
|
|
Ответ: d = 3,49 ×10-3 м.
Задача 18. Определите время t, за которое сила тока замыкания достигнет 0,8 части предельного значения, если источник ЭДС замыкают на катушку сопротивлением 10 Ом и индуктивностью 0,1 Гн.
Дано:
I = 0,8 I0;
R = 10 Ом;
L = 0,1 Гн.
Найти: t = ?
Решение: Сила тока при замыкании цепи, содержащей источник ЭДС:
|
|
|
- |
R |
×t |
|
|
|
|
|
|||
I = I |
|
- e |
|
L |
, |
|
0 1 |
|
|
|
|||
|
|
|
|
|
|
|
где |
R - сопротивление цепи, |
L - |
индуктивность, I0 - установив- |
|||||||||
шаяся сила тока. Подставив |
выражение для силы тока I = 0,8 I0 |
|||||||||||
можем записать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
R |
×t |
|
- |
R |
t |
|
|
0,8I0 |
= I |
|
- e |
L |
0,8 = 1 - e |
|
L |
. |
|||
|
0 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда искомое время
t = - L × ln 0,2 .
R
Подставляя числовые значения находим:
t = - 0,1× ln 0,2 = 16,2 ×10-3 c. 10
Ответ: t = 16,2 мс.
46
Таблица 2.1 Варианты заданий по РГР № 2.1 (в первой строке указаны предпоследняя цифра, а в первом столбце последняя цифра зачетной книжки)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
3.10 |
|
3.101 |
3.102 |
3.103 |
3.104 |
3.105 |
3.106 |
3.107 |
3.108 |
3.109 |
3.110 |
|
3.201 |
3.202 |
3.203 |
3.204 |
3.205 |
3.206 |
3.207 |
3.208 |
3.209 |
3.210 |
|
4.1 |
4.2 |
4.3 |
4.4 |
4.5 |
4.6 |
4.7 |
4.8 |
4.9 |
4.10 |
|
4.101 |
4.102 |
4.103 |
4.104 |
4.105 |
4.106 |
4.107 |
4.108 |
4.109 |
4.110 |
1 |
3.11 |
3.12 |
3.13 |
3.14 |
3.15 |
3.16 |
3.17 |
3.18 |
3.19 |
3.20 |
|
3.111 |
3.112 |
3.113 |
3.114 |
3.115 |
3.116 |
3.117 |
3.118 |
3.119 |
3.120 |
|
3.211 |
3.212 |
3.213 |
3.214 |
3.215 |
3.216 |
3.217 |
3.218 |
3.219 |
3.220 |
|
4.11 |
4.12 |
4.13 |
4.14 |
4.15 |
4.16 |
4.17 |
4.18 |
4.19 |
4.20 |
|
4.111 |
4.112 |
4.113 |
4.114 |
4.115 |
4.116 |
4.117 |
4.118 |
4.119 |
4.120 |
2 |
3.21 |
3.22 |
3.23 |
3.24 |
3.25 |
3.26 |
3.27 |
3.28 |
3.29 |
3.30 |
|
3.121 |
3.122 |
3.123 |
3.124 |
3.125 |
3.126 |
3.127 |
3.128 |
3.129 |
3.130 |
|
3.221 |
3.222 |
3.223 |
3.224 |
3.225 |
3.226 |
3.227 |
3.228 |
3.229 |
3.230 |
|
4.21 |
4.22 |
4.23 |
4.24 |
4.25 |
4.26 |
4.27 |
4.28 |
4.29 |
4.30 |
|
4.121 |
4.122 |
4.123 |
4.124 |
4.125 |
4.126 |
4.127 |
4.128 |
4.129 |
4.130 |
3 |
3.31 |
3.32 |
3.33 |
3.34 |
3.35 |
3.36 |
3.37 |
3.38 |
3.39 |
3.40 |
|
3.131 |
3.132 |
3.133 |
3.134 |
3.135 |
3.136 |
3.137 |
3.138 |
3.139 |
3.140 |
|
3.231 |
3.232 |
3.233 |
3.234 |
3.235 |
3.236 |
3.237 |
3.238 |
3.237 |
3.236 |
|
4.31 |
4.32 |
4.33 |
4.34 |
4.35 |
4.36 |
4.37 |
4.38 |
4.39 |
4.40 |
|
4.131 |
4.132 |
4.133 |
4.134 |
4.135 |
4.136 |
4.137 |
4.138 |
4.139 |
4.140 |
4 |
3.41 |
3.42 |
3.43 |
3.44 |
3.45 |
3.46 |
3.47 |
3.48 |
3.49 |
3.50 |
|
3.141 |
3.142 |
3.143 |
3.144 |
3.145 |
3.146 |
3.147 |
3.148 |
3.149 |
3.150 |
|
3.235 |
3.234 |
3.233 |
3.232 |
3.231 |
3.230 |
3.229 |
3.228 |
3.227 |
3.226 |
|
4.41 |
4.42 |
4.43 |
4.44 |
4.45 |
4.46 |
4.47 |
4.48 |
4.49 |
4.50 |
|
4.141 |
4.142 |
4.143 |
4.144 |
4.145 |
4.146 |
4.147 |
4.148 |
4.149 |
4.150 |
5 |
3.51 |
3.52 |
3.53 |
3.54 |
3.55 |
3.56 |
3.57 |
3.58 |
3.59 |
3.60 |
|
3.151 |
3.152 |
3.153 |
3.154 |
3.155 |
3.156 |
3.157 |
3.158 |
3.159 |
3.160 |
|
3.225 |
3.224 |
3.223 |
3.222 |
3.221 |
3.220 |
3.219 |
3.218 |
3.217 |
3.216 |
|
4.51 |
4.52 |
4.53 |
4.54 |
4.55 |
4.56 |
4.57 |
4.58 |
4.59 |
4.60 |
|
4.151 |
4.152 |
4.153 |
4.154 |
4.155 |
4.156 |
4.157 |
4.158 |
4.159 |
4.160 |
6 |
3.61 |
3.62 |
3.63 |
3.64 |
3.65 |
3.66 |
3.67 |
3.68 |
3.69 |
3.70 |
|
3.161 |
3.162 |
3.163 |
3.164 |
3.165 |
3.166 |
3.167 |
3.168 |
3.169 |
3.170 |
|
3.215 |
3.214 |
3.213 |
3.212 |
3.211 |
3.210 |
3.209 |
3.208 |
3.207 |
3.206 |
|
4.61 |
4.62 |
4.63 |
4.64 |
4.65 |
4.66 |
4.67 |
4.68 |
4.69 |
4.70 |
|
4.161 |
4.162 |
4.163 |
4.164 |
4.165 |
4.166 |
4.167 |
4.168 |
4.169 |
4.170 |
7 |
3.71 |
3.72 |
3.73 |
3.74 |
3.75 |
3.76 |
3.77 |
3.78 |
3.79 |
3.80 |
|
3.171 |
3.172 |
3.173 |
3.174 |
3.175 |
3.176 |
3.177 |
3.178 |
3.179 |
3.180 |
|
3.205 |
3.204 |
3.203 |
3.202 |
3.201 |
3.200 |
3.199 |
3.198 |
3.197 |
3.196 |
|
4.71 |
4.72 |
4.73 |
4.74 |
4.75 |
4.76 |
4.77 |
4.78 |
4.79 |
4.80 |
|
4.171 |
4.172 |
4.173 |
4.174 |
4.175 |
4.176 |
4.175 |
4.174 |
4.173 |
4.172 |
47
Продолжение таблицы 2.1
8 |
3.81 |
3.82 |
3.83 |
3.84 |
3.85 |
3.86 |
3.87 |
3.88 |
3.89 |
3.90 |
|
3.181 |
3.182 |
3.183 |
3.184 |
3.185 |
3.186 |
3.187 |
3.188 |
3.189 |
3.190 |
|
3.195 |
3.194 |
3.193 |
3.192 |
3.191 |
3.190 |
3.189 |
3.188 |
3.187 |
3.186 |
|
4.81 |
4.82 |
4.83 |
4.84 |
4.85 |
4.86 |
4.87 |
4.88 |
4.89 |
4.90 |
|
4.171 |
4.170 |
4.169 |
4.168 |
4.167 |
4.166 |
4.165 |
4.164 |
4.163 |
4.162 |
|
3.91 |
3.92 |
3.93 |
3.94 |
3.95 |
3.96 |
3.97 |
3.98 |
3.99 |
3.100 |
|
3.191 |
3.192 |
3.193 |
3.194 |
3.195 |
3.196 |
3.197 |
3.198 |
3.199 |
3.200 |
9 |
3.185 |
3.184 |
3.183 |
3.182 |
3.181 |
3.180 |
3.179 |
3.178 |
3.177 |
3.176 |
|
4.91 |
4.92 |
4.93 |
4.94 |
4.95 |
4.96 |
4.97 |
4.98 |
4.99 |
4.100 |
|
4.161 |
4.160 |
4.159 |
4.158 |
4.157 |
4.156 |
4.155 |
4.154 |
4.153 |
4.152 |
6 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ РГР №2.2 «Оптика. Атомная и ядерная физика»
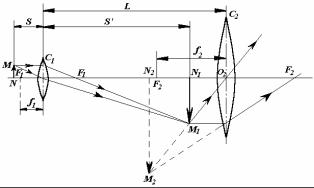
Задача 1. Фокусное расстояние объектива микроскопа F1 = 5 мм, окуляра F2 = 25 мм. Предмет находится на расстоянии s = 5,l мм от объектива (рисунок 7). Вычислить длину тубуса микроскопа и даваемое микроскопом увеличение β.
Дано:
F1= 5 мм = 5 10 -3м ; F2 =25 мм = 25 10 -3 м;
s = 5,l мм = 5,1 10 -3 м.
Найти: β=?, L=?
Решение: Увеличение микроскопа определяется по формуле
β = β1β2 , |
(1) |
где β1 - увеличение, даваемое объективом; β2 - увеличение, даваемое окуляром.
Рисунок 8 Ход лучей в микроскопе
48

Величины β1 и β2 определяются по формулам
β = |
s′ |
, |
(2) |
|||
|
||||||
|
1 |
|
F1 |
|
|
|
|
|
|
|
|
|
|
β2 |
= |
0,25 |
, |
(3) |
||
|
||||||
|
|
F2 |
|
|
|
|
где s' - расстояние от объектива до даваемого им действительного изображения, 0,25 - расстояние наилучшего видения для нормального глаза, м.
С учетом (2) и (3) формула (1) примет вид
β = |
0,25s′ |
. |
(4) |
|
|||
|
f1 f2 |
|
|
Расстояние s' от объектива до изображения можно определить из формулы линзы
1 = 1 + 1 ,
F1 s s¢
где s - расстояние от предмета до линзы. Откуда
s¢ = |
F1s |
= 0,225м. |
s - F |
||
|
1 |
|
Выпишем числовые значения величин, входящие в формулу (4), и вычислим увеличение микроскопа: s'=0,255 М; F1=5 мм =0,005м;
F2= 25 мм = 0,025 м;
β = 0,25 × 0,255 =
510.
0,005 × 0.025
Длину тубуса определим, исходя из следующих соображений. Действительное изображение, даваемое объективом, должно лежать почти в фокусе окуляра, так как окуляр действует как лупа (рисунок 8). Поэтому длина тубуса
L = s′ + F2 . |
(5) |
Подставив числовые значения в (5), вычислим длину тубуса
L = 0,255 м + 0,025 м = 0,28 м.
Если принять, что L ≈ s', то для определения увеличения микроскопа можно также пользоваться приближенной формулой:
49

β = 0,25L .
F1F2
Подставив в эту формулу числовые значения, получим
β = |
0,25 × 28 |
= 560. |
||
0,005 |
× 0,025 |
|||
|
|
|||
Ответ: β = 560 ,L = 0,28 м.
Задача 2. На плоскопараллельную прозрачную пластинку с показателем преломления 1,5 под углом 300 падает параллельный пучок белого света. Определите, при какой наименьшей толщине зеркально отраженный свет наиболее сильно окрасится в красный свет.
Дано: n = 1,5; i = 30;
λ = 670 нм = 670· 10 – 9 м;
Найти: dмин = ?
Решение: Световой луч, падающий под углом i на плоскопараллельную пластинку частично отражается и частично преломляется.
Рисунок 9 Ход лучей на плоскопараллельной пленке показателем преломления
n и толщиной d (Л – собирающая линза, Э- экран)
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки А до плоскости ОС равна:
D = ( АВ + ВС) × n - AO - λ , |
(1) |
2 |
|
50
