ЛАБОРАТОРНАЯ РАБОТА 2 2015

ЛАБОРАТОРНАЯ РАБОТА

Исследование свойств выборочного среднего

Цель работы:

Исследование статистическими методами сходимости по вероятности выборочного среднего.

Основные соотношения:

Выборочное среднее с точки зрения математической статистики есть среднее арифметическое независимых одинаково распределенных случайных величин . Следовательно, если для генеральной существуют конечные математическое ожидание и дисперсия, то для выборочного среднего справедлив закон больших чисел Чебышева.

Теорема (Закон больших чисел в форме Чебышева). Если - последовательность независимых и одинаково распределенных случайных величин, имеющих конечные математическое ожидание и дисперсию , то среднее арифметическое этих величин сходится по вероятности к их математическому ожиданию:

,

или, для любого : при .

Статистически данное утверждение можно проверить следующим образом. Генерируем последовательности случайных величин разной длины, вычисляем среднее значение для каждой последовательности и сравниваем с математическим ожиданием величин (поскольку мы сами генерируем случайные последовательности, то математическое ожидание генеральной совокупности нам известно). Если условия теоремы Чебышева выполняются, то с ростом величина отклонения выборочного среднего от математического ожидания величин должна в среднем уменьшаться. Чтобы учесть случайный характер отклонений, следует для каждой длины последовательности генерировать несколько выборок (последовательностей) значений и сравнивать либо средние значения отклонений для выборок различного объема, либо величины разброса значений . Кроме того, если наблюдается сходимость по вероятности, то всегда можно для заданной величины отклонения и вероятности определить необходимый объем выборки N, так, чтобы . Это можно сделать, например, используя центральную предельную теорему (ЦПТ). Согласно ЦПТ, если - независимые и одинаково распределенные случайных величины, имеющих конечные математическое ожидание и дисперсию , то их среднее (при ) имеет приближенно нормальное распределение с математическим ожиданием и дисперсией . Тогда:

,

где - функция Лапласа. Разрешив уравнение:

относительно n, получим необходимый объем выборки N. Определив N, можно убедиться, что величина отклонения не превышает (с вероятностью ), сгенерировав несколько последовательностей длиной N и подсчитав для каждой из них величину отклонения выборочного среднего от математического ожидания.

Если для генеральной совокупности не существует конечного математического ожидания, то сходимость выборочного среднего в этом случае не должна наблюдаться (то есть разброс значений выборочных средних в этом случае с ростом объема выборок не должен уменьшаться).

Задание.

Задан закон распределения случайной величины (приложение 1). Требуется:

a) Для каждого из , сгенерировать, используя генератор случайных чисел пакета EXCEL, по 10 выборок объемом из генеральной совокупности (для генерации случайных чисел распределенных по законам, которые отсутствуют в генераторе случайных чисел пакета EXCEL см. приложение 2). Для каждой выборки определить среднее: , данные представить в виде таблицы:

Выборочное среднее
N п/п выборки	n=15	n=60	n=240	n=960
1
2
…
10

Таблица 1. Значения выборочных средних для выборок различного объема

Оценить изменение величины разброса с ростом объема выборки. Сделать выводы о сходимости выборочных характеристик.

b) Если наблюдается сходимость выборочного среднего, используя центральную предельную теорему определить для заданной в задании (приложение 1) вероятности и величины отклонения необходимый объем выборки N, так чтобы . Проверить, сгенерировав 10 выборок найденного объема и подсчитав для каждой величину .

Примечание. Указанные в задании действия проделать для каждого из двух законов распределений, указанных в варианте задания.

Приложение 1. Варианты заданий.

Вариант 1.

1. - закон равномерной плотности на (1; 3). , .

2. - закон с плотностью распределения , ., .

Вариант 2.

1. - нормальный закон с параметрами и . , .

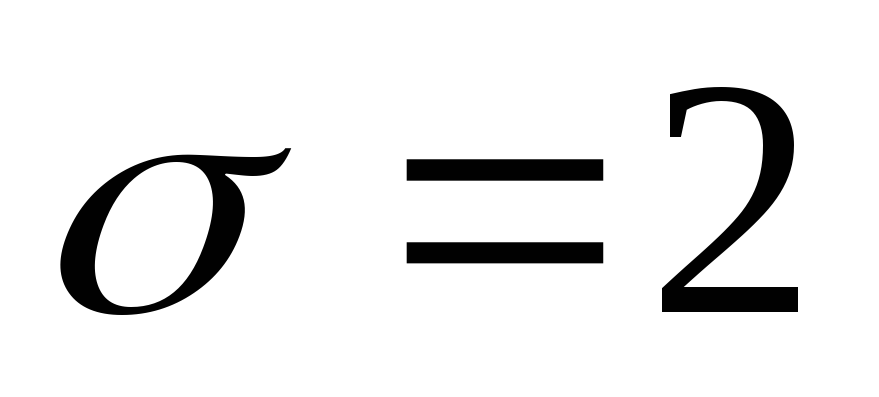2. - закон с плотностью распределения , ., .

Вариант 3.

1. - биномиальное распределение с и . , 9.

2. - закон с плотностью распределения , ., .

Вариант 4.

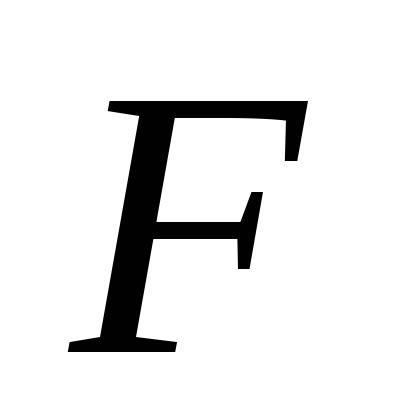1. - закон Пуассона с параметром . , .

2. - закон с плотностью распределения , . , .

Вариант 5.

1. - показательный закон с параметром . , .

2. - закон с плотностью распределения , . ,

Вариант 6.

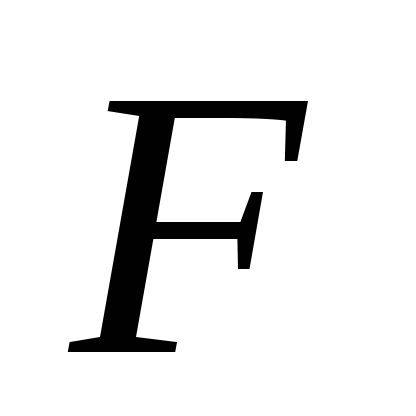1. - показательный закон с параметром. . , .

2. - закон с плотностью распределения , . , .

Вариант 7.

1. - закон Бернулли с параметром . , .

2. - закон с плотностью распределения , . , .

Вариант 8.

1. - нормальный закон с параметрами и . , .

2. - закон с плотностью распределения , . , .

Вариант 9.

1. - биномиальный закон с параметрами и . , .

2. - закон с плотностью распределения , . , .

Вариант 10.

1. - закон равномерной плотности на (-3; 3). , .

2. - закон с плотностью распределения , . , .

Вариант 11.

1. - нормальный закон с параметрами и . , .

2. - закон с плотностью распределения , ., .

Вариант 12.

1. - биномиальное распределение с и . , .

2. - закон с плотностью распределения , . , .

Вариант 13.

1. - закон Пуассона с параметром . , .

2. - закон с плотностью распределения , . , .

Вариант 14.

1. - показательный закон с параметром . , .

2. - закон с плотностью распределения , . , .

Вариант 15.

1. - нормальный закон с параметрами и. , .

2. - закон с плотностью распределения , . , .

Вариант 16.

1. - закон Бернулли с параметром . , .

2. - закон с плотностью распределения , ., .

Вариант 17.

1. - нормальный закон с параметрами и . , .

2. - закон с плотностью распределения , ., .

Вариант 18.

1. - биномиальный закон с параметрами и ., ,.

2. - закон с плотностью распределения , . , .

Вариант 19.

1. - закон равномерной плотности на . , .

2. - закон с плотностью распределения , ., .

Вариант 20.

3. - показательный закон с параметром . ,.

4. - закон с плотностью распределения , . , .

Приложение 2. Генерация случайных чисел.

Генерация случайных чисел при помощи пакета EXCEL.

Для генерации случайных чисел в пакете EXCEL 2003 выберите меню “Cервис”, “Пакет анализа”, ”Генерация случайных чисел”. Если в меню “Сервис” отсутствует подменю “Пакет анализа”, следует зайти в меню “Сервис”, “Надстройки” и подключить “Пакет анализа”. В EXCEL 2007 выберите меню “Данные”, “Анализ данных”. Если в меню “Данные” отсутствует подменю “Анализ данных”, то следует нажать кнопку “Office”, перейти в “Параметры Excel”, выбрать “Надстройки”, нажать “Перейти” и подключить “Пакет анализа”. Параметры генератора случайных чисел “число переменных” и ”число случайных чисел”. определяют соответственно число столбцов и строк для вывода случайных чисел. Можно использовать, например, “число переменных” для того, чтобы получить сразу несколько независимых выборок-столбцов объема, определяемого параметром “число случайных чисел”.

Генерация случайных чисел по законам, отсутствующим в пакете EXCEL.

Для генерации случайных чисел распределенных по законам, которые отсутствуют в генераторе случайных чисел пакета EXCEL, можно использовать следующие приемы.

1. Воспользуемся следующей теоремой из курса “Теория вероятностей”: Если случайная величина имеет непрерывную и строго монотонную функцию распределения , а величина , то , где - функция обратная к . Итак, если - функция распределения непрерывной случайной величины, для которой можно найти обратную , то генерируя случайную величину , равномерно распределенную на , получим величину с требуемой функцией распределения . Данный прием можно использовать для генерации случайных величин, распределенных по показательному закону, по закону Коши и др.

2. Если случайная величина есть композиция других случайных величин, то генерируем эти величины и строим из них искомую величину. Данный прием можно использовать, например, для получения случайных величин распределенных по законам , Стьюдента и др. Так, случайной величиной, имеющей распределение "хи-квадрат" с степенями свободы называют величину равную сумме квадратов независимых стандартных нормальных случайных величин, т.е. , . Случайной величиной , имеющей распределение Стьюдента с степенями свободы называют величину равную , где - случайная величина распределенная по закону , а - независимая от нее случайная величина распределенная по закону хи-квадрат с степенями свободы.

3. Используем “физический” смысл случайной величины. Например, случайная величина, распределенная по геометрическому закону, есть номер первого успешного испытания в бесконечной серии испытаний по схеме Бернулли. Тогда, можно сгенерировать последовательность случайных величин, распределенных по закону Бернулли, и определить порядковый номер всех единиц в этой последовательности, сбрасывая счетчик после появления каждой единицы в ноль. Последовательность номеров, очевидно, будет иметь геометрическое распределение. Приблизительно необходимую длину исходной последовательности можно оценить следующим образом: если - среднее число попыток до наступления успеха, то потребуется в среднем чисел, распределенных по закону Бернулли.