
- •Часть II
- •Введение
- •Методы сетевого планирования и управления
- •1.1.Сетевая модель и ее основные элементы
- •1.2. Параметры сетевой модели с учетом временных характеристик
- •1.3. Методы расчета параметров сетевой модели
- •Вероятностные модели систем
- •2.1. Ориентированный граф состояния системы. Марковские процессы.
- •2.2. Уравнения Колмогорова для вероятностей состояний
- •2.3. Системы массового обслуживания (смо)
- •2.3.1. Общая характеристика смо
- •2.3.2. Математическая модель однофазной смо и показатели ее эффективности.
- •2.3.3. Смо с конечной очередью
- •2.3.4. Смо с отказами
- •2.3.5. Чистая смо с ожиданием.
- •2.3.6. Смешанные системы массового обслуживания
- •2.3.7. Особенности применения моделей массового обслуживания
- •Управление запасами
- •3.1. Системы управления запасами
- •3.2.Управление запасами при детерминированном стационарном спросе
- •3.2.1. Мгновенная поставка, возникновение дефицита не допускается.
- •3.2.2.Мгновенная поставка, возникновение дефицита допускается.
- •3.2.3. Поставка с постоянной интенсивностью
- •3.3. Однокаскадные суз при вероятностном дискретном спросе
- •Методы принятия технических решений
- •4.1. Основная формальная структура принятия решений
- •4.1.1. Матрица решений
- •4.1.2.Оценочная функция
- •4.1.3.Особые случаи
- •4.2. Классические критерии принятия решений
- •4.2.1.Минимаксный критерий
- •4.2.2.Критерий Байеса —Лапласа
- •4.2.3.Критерий Сэвиджа
- •4.2.4.Расширенный минимаксный критерий
- •4.2.5.Применение классических критериев
- •4.3. Производные критерии
- •4.3.1.Критерий Гурвица
- •4.3.2.Критерий Ходжа-Лемана
- •4.3.3.Критерий Гермейера
- •4.3.4.Bl(mm)-критерий
- •4.3.5.Критерий произведений
- •4.3.6.Принятие решений согласно производным критериям
- •Литература
- •Часть II
- •191186, Санкт-Петербург, ул. Миллионная, 5
2.3.6. Смешанные системы массового обслуживания
СМО с ограниченным временем ожидания характеризуется тем, что уменьшение числа заявок в ней происходит как в результате завершения обслуживания одной из заявок, так и в результате ухода заявок из очереди с интенсивностьюv.
Если число заявок в системе k<n,то k,k-1=k.. Если в очереди имеетсяrзаявок(k=n+r),то переход из состоянияSkв состояниеSk-1осуществляется или в результате завершения обслуживания одной изпзаявок, или в результате ухода из очереди одной изrзаявок, то есть

Таким образом, для СМО с ограниченным временем ожидания
![]() (2.45)
(2.45)
Граф состояний системы изображен на рис. 2.6(п=2).
Подставляя выражения (2.45)в формулы (2.16)и 2.17),как и в случае СМО с конечной очередью, получим
 (2.46)
(2.46)
![]() (2.47)
(2.47)

 . (2.48)
. (2.48)
Определим основные показатели эффективности системы. Средняя длина очереди
 (2.49)
(2.49)
На каждую из Lзаявок, находящихся в очереди, действует поток уходов интенсивностиv, то есть в среднем в единицу времени из очереди уходитLvзаявок. Следовательно, абсолютная пропускная способность
![]() ; (2.50)
; (2.50)
относительная пропускная способность
![]() (2.51)
(2.51)
вероятность отказа в обслуживании
![]() ; (2.52)
; (2.52)
среднее число занятых приборов
![]() ; (2.53)
; (2.53)
вероятность того, что любая заявка будет обслужена,
![]()
![]() (2.54)
(2.54)
При вычислениях в формулах (2.46)и (2.49)в качестве приближенного значения для бесконечных сумм берется сумма конечного числа l–1членов, а остаток оценивается следующим образом :
 .
.
Из выражений (2.50) – (2.54)следует, что основные показатели СМО можно вычислить черезРотк, причём для определенияРоткиспользуют таблицы с тремя входами:n, , .
СМО с ограниченным временем пребыванияхарактеризуется тем, что заявка может уйти необслуженной как из очереди, так и после начала обслуживания. Интенсивность перехода данной системы из состоянияSkвSk-1(уменьшения числа заявок)
Подставляя выражения (2.9)и (2.55)в формулы (2.16)и(2.17),можно определить вероятности состояний данной системы.
Если
одновременно накладывается ограничение
на время ожидания (пребывания) и длину
очереди, то число состояний системы
конечно и равно п+т+1, аинтенсивности
переходов определяются формулами
(2.45)или (2.55),в которыхr= 1, 2, . . .,т.Типичным примером системы
данного типа является вычислительное
устройство, которое может одновременно
обрабатыватьпсообщений и имеет
буферную память для хранениятсообщений. Поток сообщений
–простейший поток интенсивности,время
обработки одного сообщения
![]() ,информация теряет свою ценность через
время
,информация теряет свою ценность через
время
![]() .Граф состояний для случаяn=2,m=3 изображен на рис.
2
.Граф состояний для случаяn=2,m=3 изображен на рис.
2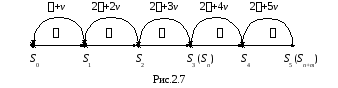 .7.
.7.
2.3.7. Особенности применения моделей массового обслуживания
Рассмотренные модели массового обслуживания находят широкое применение при исследовании надежности технических систем, организации их эксплуатации и использования по назначению, а также при анализе и синтезе автоматизированных систем управления. Достаточно подробно вопросы практического применения моделей СМО рассмотрены в работе [1].
При решении прикладных задач необходимо прежде всего правильно определить, насколько аппроксимирующие предположения, принятые при разработке математических моделей СМО, приемлемы для реальной системы и каким образом ее специфические особенности можно учесть в типовой модели.
Основными аппроксимирующими предположениями при разработке моделей СМО были предположения о том, что все потоки событий являются простейшими. Широкое использование указанных предположений обусловливается следующими факторами.
1.Простейший поток событий, как уже отмечалось, носит предельный характер и поэтому часто встречается в практических задачах. Так, например, Н. М. Седякин показал, что поток отказов элементов технических систем сводится к простейшему, если
 , (2.56)
, (2.56)
где ti –среднее время наработки i-гоэлемента данного типа на отказ, ап – число элементов. Еслиn>10, то это условие выполняется и тогда, когда каждый из элементов отказывает через постоянные интервалы времени.
2.Простейший поток заявок ставит СМО в наиболее тяжелые условия. И. Н. Коваленко показал, что система, рассчитанная на обслуживание простейшего потока, будет обслуживать любой другой поток с одинаковой интенсивностью более надежно.
3.При простейшем потоке заявок показатели эффективности СМО с отказами и ограниченным временем ожидания практически не зависят от вида закона распределения времени обслуживания, а определяются его средним значением. Показатели эффективности реальной СМО при простейшем потоке заявок не хуже значений этих показателей, вычисленных в предположении об экспоненциальном распределении времени обслуживания.
4.При указанных предположениях можно получить аналитическую модель системы и на основе ее исследования найти ее оптимальные параметры. Простая модель позволяет разобраться в основных закономерностях явления, наметить «ориентиры» для построения статистической модели системы, позволяющей учесть те особенности реальной системы, которые трудно (или невозможно) учесть при аналитическом исследовании. Сочетание простых аналитических моделей и статистического моделирования вероятностных систем на ЭВМ —один из основных методов современного научного исследования.
При решении прикладных задач всегда необходимо учитывать возможность использования результатов исследования стационарного режима для оценки эффективности системы на конечных интервалах времени. Характеристики стационарного режима с достаточной для практики точностью можно использовать для процессов длительностью (34)1/ [1].
При исследовании СМО предполагалось, что обслуживающие приборы абсолютно надежны. Если вероятность успешного обслуживания заявки Р<1, то ее влияние на эффективность СМО можно учесть черезPоткВ этом случае
![]() ,
,
где Р0отк —вероятность отказа для системы с абсолютно надежными приборами (Р=1).
Все рассмотренные модели СМО относятся к классу так называемых разомкнутых систем, в которые поступает неограниченный поток заявок и его параметры не зависят от процесса обслуживания. Однако на практике часто встречаются системы, когда поток заявок ограничен и его параметры зависят от процесса обслуживания (замкнутые системы).
Типичным примером замкнутой системы является следующая система. Имеется премонтных мастерских, которые предназначены для обслуживания и ремонтаттехнических систем. Технические системы отказывают только в период эксплуатации с интенсивностью(в период ремонта =0),производительность каждой мастерской. Число возможных состояний данной системыm+1 (k=0, 1, 2, ...,т – число технических систем, требующих ремонта). Граф состояний данной системы дляп=2, т=5 (рис. 2.8)свидетельствует о том, что для ее исследования нельзя использовать ни одну из рассмотренных моделей СМО. При ее исследовании необходимо непосредственно использовать выражения(2.16)и (2.17)для процесса «гибели и размножения».
П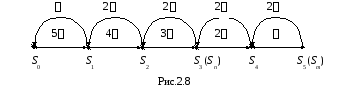 риведенный
пример показывает, что при выборе модели
СМО для решения конкретной задачи ошибки
можно исключить, если построить
размеченный граф состояний. На основе
анализа размеченного графа состояний
в некоторых случаях можно установить,
что для исследования системы, по
формальным признакам не относящейся
к системам массового обслуживания,
можно использовать одну из известных
моделей СМО.
риведенный
пример показывает, что при выборе модели
СМО для решения конкретной задачи ошибки
можно исключить, если построить
размеченный граф состояний. На основе
анализа размеченного графа состояний
в некоторых случаях можно установить,
что для исследования системы, по
формальным признакам не относящейся
к системам массового обслуживания,
можно использовать одну из известных
моделей СМО.
При
решении прикладных задач следует также
всегда отличать показатели эффективности
L,
![]() от ограничений, накладываемых на
параметры СМО:т,
от ограничений, накладываемых на
параметры СМО:т,
![]() .
ПоказателиL,
.
ПоказателиL,
![]() используются для оценки эффективности
СМО, а параметрыт,
используются для оценки эффективности
СМО, а параметрыт,
![]() определяются спецификой процесса
обслуживания и физическими свойствами
заявок (например, емкость хранилищ в
ремонтном органе, время старения
информации и так далее).
определяются спецификой процесса
обслуживания и физическими свойствами
заявок (например, емкость хранилищ в
ремонтном органе, время старения
информации и так далее).
Задачи, решаемые с помощью моделей СМО, можно разделить на два основных класса. К первому классу относятся задачи анализа эффективности систем и определения числа обслуживающих приборов, обеспечивающих требуемые значения показателей ее эффективности. Ко второму классу относятся задачи определения числа и типа (производительности) обслуживающих приборов.
