МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕСИОНАЛЬНОГО ОБРАЗОВАНИЯ

ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

Кафедра физики

Лаборатория механики и молекулярной физики №1(213а)

Лабораторная работа №7

ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ УПРУГИХ КОЛЕБАНИЙ

Отредактировал: Воронцова Е.Н.

Ижевск 2011

ЛАБОРАТОРНАЯ РАБОТА №7

ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ УПРУГИХ КОЛЕБАНИЙ

Цель работы: Определение эффективной массы пружины, установление зависимости периода упругих колебаний от массы. Определение жёсткости пружины.

Приборы и принадлежности: 1) спиральная пружина с кронштейном, 2) набор грузов, 3) электросекундомер.

Рис. 1.

При колебаниях тело совершает движения, периодически возвращающиеся к положению равновесия. Время Т, в течение которого совершается полное колебание, называется периодом колебания. При простом гармоническом колебании смещение x (рис.1) тела от положения равновесия определяется уравнением x =Аsin t, где А – амплитуда колебания,  – циклическая частота колебания,  =2 = 2/Т (1). Амплитуда колебания – наибольшее смещение точки (тела) от положения равновесия. Скорость V при колебательном движении вычисляется методом математического анализа, как производная смещения x по времени: V = . Ускорение при колебательном движении определяется как первая производная скорости V по времени:

Сила, вызывающая колебание, периодически возвращает тело в положение равновесия и поэтому называется возвращающей силой. По второму закону динамики можно написать:

F = ma = – m²x.

Если тело массой m совершает колебания на пружине, то в этом случае возвращающая сила определяется упругими свойствами пружины.

По закону упругих деформаций (закон Гука) между силой упругости и величиной деформации существует зависимость F = - kx, где k –коэффициент жёсткости пружины, знак «-» показывает, что сила F по направлению противоположна смещению x. Приравняв силы, имеем:

- m²x = - kx, т.е. m² = k (2)

откуда .

Подставляя в формулу (2) значение из (1) получим:

Откуда получим период упругих колебаний: (3)

Из этого выражения выразим коэффициент жёсткости:

(4)

При выводе этих уравнений предполагалась невесомость самой пружины. Однако надо считаться с тем, что на практике реальные пружины имеют довольно заметную массу, учёт которой осложняется тем обстоятельством, что масса пружины не сосредоточена на каком-то её конце, например, а более или менее равномерно распределена по всей её длине. В этом случае можно ввести понятие эффективной (действующей) массы пружины следующим образом: если известна жёсткость пружины k, то эффективной массой пружины назовём величину

г

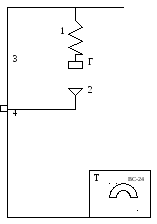
Рис. 2. Установка для изучения упругих колебаний

де Т₀ – период свободных колебаний пружины под действием её собственной силы тяжести (т.е. без грузов и подвеса). В статистическом случае можно эффективную массу определить теоретически. Расчёт даёт

m₀ = 1/2m_пруж, что соответствует и интуитивным соображениям, поскольку пружина растягивается в основном под действием веса её нижней части. В работеm₀ определяется экспериментально. Измерив период колебаний ненагруженной пружины Т₀ , а затем период колебаний Т_п пружины с подвесом массой m_п можно дважды записать выражение (4):

откуда следует: ,

окончательно (5)

где обозначено гдеm_п – масса подвеса.

Используемая в работе установка состоит из спиральной пружины 1, один конец которой жёстко соединён с кронштейном и электромагнита 2, перемещающегося по стойке 3 и закреплённого к стойке с помощью крепления 4 (рис.2). На конце пружины имеется крюк для подвешивания грузов 5.

Под величиной массы m колеблющегося тела в этой установке следует понимать массу подвеса и подвешенных грузов и эффективную массу пружины.