Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Удмуртский государственный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Reshenie tip priemov po matematike_ochnaya

.pdf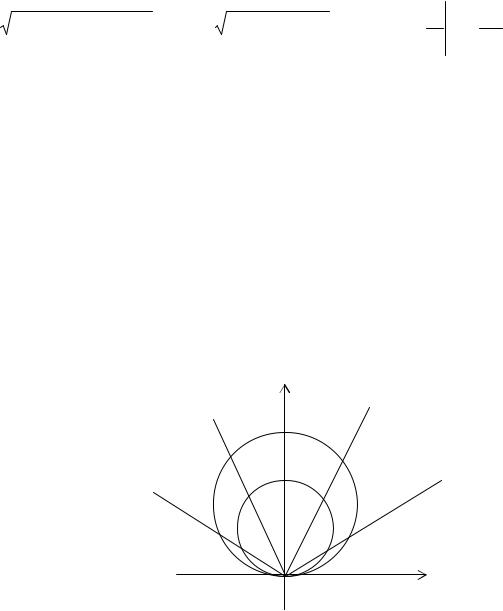

Скачиваний:

Добавлен:

29.05.2015

Размер:

581 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

xt′ = 2t sin t + (t 2 − 2)cost + 2cost − 2t sin t = (t 2 − 2 + 2)cost = t 2 cost,

yt′ = −2t cost + (2 −t 2 )(−sin t) + 2sin t + 2t cost = (−2 +t 2 + 2)sin t = t 2 sin t.

Вычислим длину дуги при 0 ≤t ≤π :

π			π	π		π
π			π	π
l = ∫ t 4 cos2 t +t 4 sin 2 tdt = ∫t 2 cos2 t +sin 2 tdt = ∫t 2dt = t3							=	π 3	ед.
0			0	0	3 0			3
Ответ: l =	π	3	ед.
Ответ: l =	3		ед.
	3
б) Вычислить площадь				фигуры, ограниченной				кривыми
ρ = 6sinϕ , ρ = 4sinϕ , заданными в полярной системе координат.

Решение. Площадь фигуры, ограниченной одной или двумя кривыми, заданными в полярной системе координат, вычисляется по формулам

S =	1	ϕ2	ρ2	(ϕ)dϕ или S =	1 ϕ2	(ρ22	(ϕ)− ρ12 (ϕ))dϕ .

	2	ϕ∫			2 ϕ∫

		1			1

Сделаем чертеж искомой площади, учитывая, что ρ ≥ 0 , поэтому sinϕ ≥ 0 , то есть 0 ≤ϕ ≤π .

π/2

π/3

π/6

ρ1 = 4sinϕ , ρ2 = 6sinϕ .

Так как фигура симметрична относительно прямой ϕ = π2 , то

		π			π
S = 2S = 2	1	2	(ρ2 (ϕ)− ρ2 (ϕ))dϕ =		2	(36sin2 ϕ −16sin2 ϕ)dϕ =
	2	∫			∫
1			2	1
		0			0

π						π							π		π
2						2								2	2
= 20∫sin 2 ϕdϕ =10						∫(1−cos 2ϕ)dϕ					=10			∫dϕ − ∫cos 2ϕdϕ				=
0						0									0
0						0							0		0

		π				π
				1		2		π			1					π
				1		2		π			1					π
=10	ϕ	2	−		sin 2ϕ		=10		−0	−		(0	−0)		=10		= 5π.
=10	ϕ	2	−		sin 2ϕ		=10		−0	−		(0	−0)		=10		= 5π.
		0		2			2				2					2
		0				0
						0

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №4

12. Найти частное решение дифференциального уравнения второго порядка, допускающее понижение порядка (х2 +1)у′′ = 2ху′, удовлетво-

′	=3.
ряющее указанным начальным условиям у(0) =1, у (0)

Решение. Данное дифференциальное уравнение второго порядка не содержит явно функцию у. Положим у′ = р, где р – некоторая функ-

											dp
ция аргумента х. Если у′ = р, то											у′′ = dx , и данное уравнение примет
вид (x2 +1)						dp		= 2xp . Мы получили уравнение первого порядка относи-

						dx
тельно переменных р и х. Решим это уравнение:
	dp		=		2xdx				;
	p					x2 +1
	∫	dp		= ∫			2xdx			;
		p					2
								x +1
ln p = ln(x2 +1)+ ln C ,
				1

p = C1(x2 +1), или y′ = C1 (x2 +1).

Определим численное значение С1 при указанных начальных условиях. Имеем 3 = C1 (0 +1) . Следовательно, C1 = 3 . Теперь решаем уравнение

первого порядка y′ = 3(x2 +1): dy = 3(x2 +1)dx;

y = 3∫(x2 +1)dx =x3 +3x +C2 .

Определим численное значение С2 при указанных начальных условиях.

Имеем 1 = 0 + 0 + С2 ;	С2 =1.
Таким образом,	у = x3 +3x +1 есть частное решение, удовлетво-

ряющее указанным начальным условиям.

13. Найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами у′′+ 4у = 4sin 2x −8cos 2x , удовлетворяющее указанным начальным ус-

ловиям y(0) = 0, y′(0) = 0 .

Решение. Общее решение у данного уравнения равно сумме общего решения уодн однородного уравнения и какого-либо частного решения у данного уравнения, то есть

у = уодн + у.

Для нахождения уодн составим характеристическое уравнение k 2 + 4 = 0 , имеющее комплексные корни k1 = 2i, k2 = −2i . В этом случае

общее решение однородного уравнения ищем в виде

уодн = eαx (C1 cos βx +C2 sin βx),

где α ± βi – комплексные корни характеристического уравнения. Подставив α = 0, β = 2 , имеем:

уодн = C1 cos 2x +C2 sin 2x .

Частное решение у неоднородного дифференциального уравнения ищем в виде y = xeαx (Acos βx + Bsin βx) , так как правая часть неодно-

родного уравнения есть функция f (x) = eαx (a cos βx +bsin βx)								и числа
α ± βi	являются				корнями характеристического		уравнения. При
α = 0, β = 2 имеем:
y = x(Acos 2x + B sin 2x) .
Дважды дифференцируя последнее равенство, находим y′′:
y′′ = (4B −4Ax) cos 2x + (−4A −4Bx) sin 2x .
Подставив в данное уравнение y и y′′, получим:
4B cos 2x − 4Asin 2x = 4sin 2x −8cos 2x ,
откуда A = −1, B = −2 . Следовательно, y = −x(cos 2x + 2sin 2x) и
у = C1 cos 2x +C2 sin 2x − x(cos 2x + 2sin 2x) .
Найдем y′:
у′ = −2C1 sin 2x + 2C2 cos 2x −cos 2x − 2sin 2x − x(−2sin 2x + 4cos 2x) .
Используя начальные условия, получим систему
C = 0,
	1
2C2 −1 = 0,				1
откуда	C = 0, C	2	=	1		.
откуда	C = 0, C		=			.
	1			2
				2		1 sin 2x − x(cos 2x + 2sin 2x) есть
Следовательно,			у =			1 sin 2x − x(cos 2x + 2sin 2x) есть	искомое	частное
					2

решение данного дифференциального уравнения.

14. Классическим методом и методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.

х′−3х− 4у = 0,у′− 4х+3у = 0,

х(0) = у(0) =1.

Решение. Решением этой системы является пара функций х(t) , y(t) , удовлетворяющих системе, причем х(0) = у(0) =1.

1) Классический метод решения.

Продифференцируем первое уравнение по переменной t : x′′−3x′− 4 y′ = 0 .

Из первого уравнения определяем

y =

x′−3x

, следовательно, из второго

уравнения имеем

x′−3x

25x 3x′

′

= 4x

−3y

= 4x −3 4 = 4 − 4 .

Подставляем

y′

в уравнение, полученное после дифференцирования,

приходим к уравнению

3x′

25x

−

x′′−3x′− 4

= 0 ,

x′′− 25x = 0 – линейное дифференциальное уравнение II порядка с постоянными коэффициентами.

Составляем характеристическое уравнение и находим его корни: k 2 −25 = 0,

k 2 = 25,

k1,2 = ±5 – действительные различные корни.

В этом случае общее решение дифференциального уравнения имеет вид

x(t) = C ek1t

ek2t ,

x(t) = C e5t

e−5t .

x′−3x

Ранее определили

y =

. Тогда

e−5t )

5C e5t −5C

e−5t −3(C e5t + C

е5t − 2C2e

−

5t .

y =

Общее решение системы

x(t)

= C e5t + C

e−5t ,

С1

е5t − 2C2e−5t .

y(t)

Находим значения произвольных постоянных, используя начальные условия х(0) = у(0) =1:

1 =	С	+		С			,						С			=	6		,
1 =	С	+		С			,						С			=			,
	1					2									1	5
1 =	С1		−2С						,										1
1 =			−2С						,										1
								2
	2												С2			= −			5	.
																			5
Частное решение системы
		6			5t					1		−5t
x(t) =				e				−			e			,
x(t) =		5		e				−		5	e			,
		5								5
		3								2
		3			5t					2					−5t
y(t) =				е				+			C2e					.
y(t) =		5		е				+		5	C2e					.
		5								5
2) Метод операционного исчисления.
Пусть х(t) =••								X ( p),							y(t) =••			Y ( p) . По теореме о дифференцировании
оригинала получим
′	•
х (t) =• pX ( p) − x(0) = pX ( p) −1,
′	•

y (t) = pY ( p) − y(0) = pY ( p) −1.

•

Следовательно, операторная (изображающая) система имеет вид:

pX ( p) −1−3X ( p) −4Y ( p) = 0,pY ( p) −1− 4X ( p) +3Y ( p) = 0.

Из первого уравнения определяем Y ( p) =

pX ( p) −3X ( p) −1

и подстав-

ляем во второе уравнение:

p(pX ( p) −3X ( p) −1)

−1− 4X ( p) + 3(pX ( p) −3X ( p) −1)= 0,

p2 X ( p) −25X ( p) − p −7 = 0,

X ( p) =

p + 7

X ( p) =

p +7

− 25

( p

−5)( p +

Представим дробь в виде суммы простых дробей:

p + 7

( p −5)( p +5)

p −5

p +5

p + 7 = A( p +5) + B( p −5),

p =5: 12 =10A,

A =

6 ,

p = −5 : 2 = −10B,

B = −

Следовательно, X ( p) =																	6				1		−	1
Следовательно, X ( p) =																					p −5		−	5
																5					p −5			5
По таблице изображений находим
x(t) =		6		e	5t		−		1			e			−5t			.
x(t) =		5		e			−		5			e						.
		5							5
Аналогично:					p +1
Y ( p) =					p +1								,
Y ( p) =				p	2 −25								,
				p	2 −25
Y ( p) =			3					1					+			2				1		,
Y ( p) =			5			p		−5					+			5				p +5		,
			5			p		−5								5				p +5
y(t) =		3		e	5t		+		2				e		−5t			.
y(t) =		5		e			+		5				e					.
		5							5
Частное решение системы
			6			5t				1						−5t
x(t) =					e			−						e					,
x(t) =			5		e			−		5				e					,
			5							5
				3							2
				3		5t					2					−5t
y(t)	=				e			+							e				.
y(t)	=			5	e			+			5				e				.
				5							5

15. Найти изображение F( p) ,

ски.

p +5 .

если оригинал f (t) задан графиче-

f(t)
3		А	В
3				D
2			С	D
2			С
О	α
0		2	4	t
Решение. f (t) = f1 (t) + f2 (t) + f3 (t) , где				f1 (t) – уравнение отрезка
ОА, f2 (t) – отрезка АВ и		f3 (t) – прямой СD.

Для того, чтобы записать оригинал f1(t) , предварительно найдем уравнение прямой ОА. Так как она проходит через начало координат и

имеет угловой коэффициент k = tgα = 32 , то ее уравнение y = 32 t . Выре-

жем из нее отрезок ОА с помощью единичного прямоугольного импульса (σ(t) −σ(t −2)), где σ(t) – единичная функция Хевисайда, а σ(t − 2) –

запаздывающая на две единицы. Тогда оригинал, соответствующий отрезку ОА, запишется в виде

f1(t) = 23 t (σ(t) −σ(t − 2)).

Оригинал, соответствующий отрезку АВ – это прямоугольный импульс высотой 3, то есть

f2 (t) = 3(σ(t −2) −σ(t − 4)).

Прямой CD соответствует запаздывающая на 4 функция Хевисайда высотой 2, то есть

3 f1(t) = 2σ(t − 4) .

Итак:

f (t) =	3 t (σ(t) −σ(t − 2))+3(σ(t − 2) −σ(t − 4))+ 2σ(t − 4)
или	2
или	3			3
	3			3
f (t) =		t σ(t) +	−		t +3 σ(t −2)	−σ(t −4) .
f (t) =	2	t σ(t) +	−	2	t +3 σ(t −2)	−σ(t −4) .
	2			2

Первое и третье слагаемые табличные. Подведем под табличные формулы второе слагаемое.

	−	3					3	(t − 2)σ(t − 2) .
	−	2	t +3 σ(t − 2) = −				2	(t − 2)σ(t − 2) .
		2					2
Тогда				3 t σ(t) −	3
f (t) =				3 t σ(t) −	3	(t − 2)σ(t − 2) −σ(t − 4) .
				2	2

По таблицам находим изображение, учитывая, что второе слагаемое опаздывает на 2 единицы, а третье – на четыре.

F( p) =

−

e−2 p −

e−4 p

Ответ:

F( p) =

−3e−2 p − 2 pe−4 p

2 p2

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №5

16. Найти интервал сходимости степенного ряда

выяснить вопрос о сходимости ряда на концах интервала.

	Решение. Введем				новое	переменное		t = x −5 и
∞	t	n			1			1
∑			, где an =			и an+1	=
	(2n −1)3n			(2n −1)3n
n=1							(2(n +1) −1)3n+1

Найдем радиус сходимости степенного ряда

∑∞ (x −5)n и

n=1 (2n −1)3n

получим ряд

= +1 n+1 . (2n 1)3

1 (2n +1) 3n 3

2n +1

n 2

R = lim

= lim

3 lim

= 3 lim

= 3

(2n −1)

2n −1

n→∞

n+1

n→∞

n 2

−

∞

Таким образом, интервал сходимости ряда ∑

(–3; 3), то есть

t (−3;3) .

n=1 (2n −1)3n

Выясним вопрос о сходимости этого ряда на концах интервала.

При t = −3 ряд принимает вид

∞

(−3)

∞

(−1)

∞

(−1)

∑

=∑

(2n −1)3n

2n −1

n=1

Получили числовой знакочередующийся ряд, применим к нему признак Лейбница:

lim an

= lim

= 0,

2n −1

n→∞

∞

a > a

> a

>..., в самом деле, 1 > 1 > 1 > 1 >...

Значит, ряд сходится и t = −3 – точка сходимости ряда.

∞

При t = 3

получаем ряд ∑

(u) . Сравним его с гармониче-

∞

n=1 2n −1

ским рядом (v)

∑

, который расходится. Применим предельный при-

n=1 n

знак сравнения.

lim

= lim

1 n

= lim

≠ 0.

n→∞ v

n→∞ (2n −1)

n→∞

n 2 −

∞	1
Значит, оба ряда ведут себя одинаково, то есть ряд (u) ∑	1	расхо-
Значит, оба ряда ведут себя одинаково, то есть ряд (u) ∑	2n −1	расхо-
n=1	2n −1

дится и t = 3 – точка расходимости.

∞

Таким образом, область сходимости для ряда ∑

n=1

−3	≤ t < 3.
Перейдем к переменному х:
−3	≤ x −5 < 3 или 5 −3 ≤ x < 5 +3; 2 ≤ x < 8 .

Ответ: Область сходимости x [2;8).

t n

(2n −1)3n

17. Разложить заданную функцию f (x) = π4 − 12 х в ряд Фурье по

синусам на отрезке [0;π] и построить результирующую первых двух гармоник полученного ряда.

Решение. Так как по условию ряд должен содержать только синусы кратных углов, то следует продолжить заданную функцию на отрезок [−π;0] нечетным образом, затем продолжить на всю числовую ось с периодом Т = 2l = 2π . Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:

a20 + ∑∞ (an cos nx +bn sin nx).

n=1

Так как

заданная

функция нечетная, то коэффициенты ряда Фурье

a0 = 0, an = 0 , а bn

вычисляем по формуле

bn =

∫ f (x) sin nxdx

(n =1,2,...)

∞

и ряд Фурье имеет вид ∑bn sin nx .

n=1

Подставляя заданную функцию, получаем

(π − 2x)sin nxdx .

−

x sin nxdx =

2π ∫

∫

Последний интеграл вычисляем методом интегрирования по частям, полагая u =π − 2x, dv = sin nxdx . Отсюда

du = −2dx, v = ∫sin nxdx = −

1 cos nx . Следовательно,

cos nx

bn =

−(π − 2x)

∫cos nxdx

−

2π

−π cosπn

−

sin nx

−

2π

(cosπn +1)−

(sinπn −sin 0)

2π

0, еслип−нечетное,

(cosπn +1)=

2π

еслип

− четное.

Таким образом, искомое разложение имеет вид

π −		1			х = b sin x +b										sin 2x +b							sin 3x +b					sin 4x +b sin 5x +
π −					х = b sin x +b										sin 2x +b							sin 3x +b					sin 4x +b sin 5x +
4	2						1						2						3							4						5
4	2																	1											1
+b		sin 6x +... = 0 sin x +																1	sin 2x +0 sin 3x +										1	sin 4x + 0 sin 5x +...
+b		sin 6x +... = 0 sin x +																	sin 2x +0 sin 3x +											sin 4x + 0 sin 5x +...
6																		2									4
или																		2									4
или					π			− 1 х =			1							1
					π			− 1 х =			1		sin 2x +					1	sin 4x +...
	4						2				2							4
					В					полученном							разложении							возьмем						первые				две гармоники:
y =				1		sin 2x ,					y	2	=	1	sin 4x ; построим их графики; путем сложения y																							и
y =						sin 2x ,					y		=		sin 4x ; построим их графики; путем сложения y																							и
1	2												4																								1
y2 построим график результирующей																										y* = y1 + y2 и данной функции
y =	π −						1 х на отрезке [0;π].
	4						2
							у
0,78 ≈ π																у = π −				1	х
0,78 ≈ π																у = π −					х
							4											4	2
	0,5 =								1
	0,5 =						2
							2
	1/4
							0				π			π			π		π			3π		π				2π				3π	5π				π	х
							0				8		6				4		3			8		2			3					4	6				π	х
											8		6				4		3			8		2			3					4	6
						–1/4
–0,5 = –								1
–0,5 = –
							2
–0,78 ≈ – π
							4
y =			1		sin 2x (– – – – – )										y		=	1	sin 4x (							)		y* =			1	sin 2x +		1	sin 4x (–×––×––×–)
y =					sin 2x (– – – – – )										y	2	=		sin 4x (							)		y* =				sin 2x +			sin 4x (–×––×––×–)
1	2															2		4													2		4
	2																	4													2		4
					18. а) Найти разложение в степенной ряд																											по степеням х решения
дифференциального уравнения																						y	′′	= xy	′	− y + e				x	,					′	= 0 (запи-
дифференциального уравнения																						y		= xy		− y + e					,	y(0) =1, y (0)					= 0 (запи-

сать три первых, отличных от нуля, члена этого разложения).

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.04.20252 Мб3R_12.doc
#
29.05.20151 Мб28Rabochaya_tetrad_molochnoe_delo.doc
#
20.11.2018389 Кб26Ramka_dlya_texta.doc
#
20.08.2019456 Кб7Rastenievodstvo_MetodUkazan-Samost-Agro.doc
#
08.11.201995 Кб9Razvivayushiesya_strany-sovremennoe_sostoyanie_...docx
#
29.05.2015581 Кб11Reshenie tip priemov po matematike_ochnaya.pdf
#
01.07.2025170 Кб1Rezhim_obzhiga.doc
#
25.03.20162 Мб13rgr_-_kopia.doc
#
08.11.2019223 Кб6Rossia_v_mirovom_hozyaystve-sovremennyy_etap_pr...docx
#
14.09.201936 Кб16Russky_yaz_1_2.docx
#
26.11.2019406 Кб12Russky_yazyk_Praktikum.rtf