1.Краткие теоретические сведения.

При изучении автоматических систем широко применяют классификацию элементов по динамическим свойствам. Это позволяет все многообразие физических устройств, из которых состоят автоматические системы, представить сравнительно небольшим числом типовых динамических звеньев. Под элементарным звеном понимают звено, описывающееся дифференциальным уравнением не выше второго порядка; выделяют следующие типовые устойчивые элементарные звенья: усилительное или безинерционное, дифференцирующее, интегрирующее, апериодическое 1-ого порядка или инерционное колебательное, апериодическое 2-ого порядка, консервативное, форсирующее, звено запаздывания.

Интегрирующее звено описывается уравнениями:

(1)

или (2)

При подаче на вход И-звена ступенчатого воздействия («скачка»)

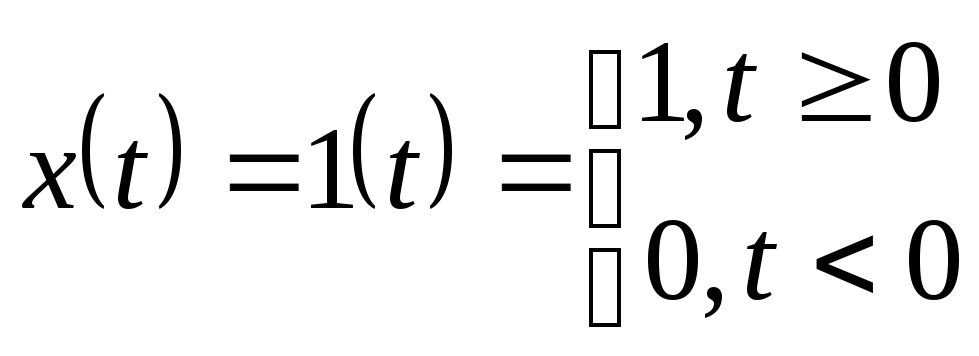(3)

получаем графики (рис.1). Другими словами, при подстановке (3) в (1) имеем решение (1) в виде:

(4)

т.е. получаем тот же график прямой линии с углом наклона β (рис.1)

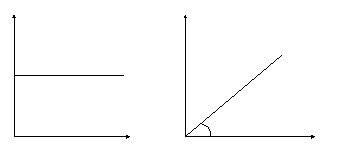
x(t) y(t)

1

β

t t

Рис.1

Изображение уравнения (1) оп Лапласу при нулевых начальных условиях дает операторное уравнение:

и передаточную функцию И-звена:

(5)

где Yp), X(p) – изображение по Лапласу функций y(t) и x(t),

p=α+jω - комплексная переменная

(буквой «р» обозначается также оператор дифференцирования,

- оператор интегрирования),

- постоянная времени интегрирующего звена.

Подставляя в (5) р=jω, получим частотные характеристики И-звена.

Амплитудно-фазо-частотная характеристика (АФЧХ)

(6)

Амплитудно-частотная характеристика (АЧХ)

(7)

Фазо-частотная характеристика (ФЧХ).

(8)

Частотные характеристики И-звена изображены на рис.2

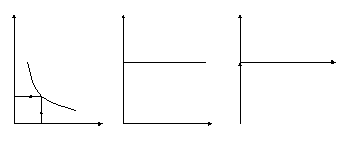
W(ω) φ(ω) jIm(ω)

Re(ω)

0 ω ω=∞

W(ωi) W_и(jω)

ω=0

ω_i ω

Рис.2

По экспериментально снятой временной характеристике (4) можно определить k_и=tgβ и вычислить , используя (6) – (8), построить частотные характеристики И-звена.

Апериодическое звено 1-ого порядка

Апериодическое звено 1-ого порядка описывается дифференциальным уравнением 1-ого порядка.

, (9)

где T и k –постоянная времени и коэффициент передачи А1-звена.

Решение уравнения (9) имеет вид:

(10)

Поэтому (10) имеет вид, показанный на рис.3.

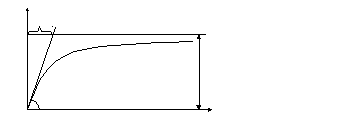y(t)

T

K

β

t

Рис.3.

При определении T учитывалось также, что весь переходный процесс А1-звена продолжается (4-5)T.

Применяя к (9) преобразования Лапласа при нулевых начальных условиях, имеем:

откуда имеем выражение для передаточной функции:

(11)

Подставляя в (11) p=jω получаем частотные характеристики А1-звена

-АФЧХ, (12)

-АЧХ (13)

,- ФЧХ (14)

Частотные характеристики представлены на рис.4

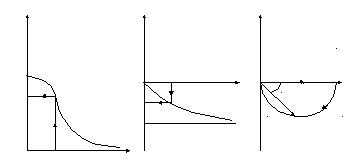
W(ω) φ(ω) jIm(ω)

ω k/2 Re(ω)

k/√2 0 ω=∞ 45˚ ω=0

π/2

0 ω=1/Т ω

Рис.4

По экспериментально снятой временной характеристике можно определить k и постоянную времени звена T , используя (12)-(14), построить частотные характеристики А1-звена.

Колебательное звено

Колебательное звено описывается дифференциальным уравнением второго порядка

, (15)

где 0<ξ<1- коэффициент затухания или демпфирования;

T-постоянная времени,

k- коэффициент передачи.

при ξ=0 уравнение (15) описывает апериодическое звено, имеющее незатухающие колебания;

при ξ≥1 уравнение (15) описывает апериодическое звено второго порядка, колебания на выходе которого отсутствуют.

Решение (15) при 0<ξ<1 имеет вид:

, (16)

где ω_* - мнимая часть корня характеристического уравнения, соответствующего (15); сами корни можно обозначить

- относительное демпфирование (см. рис.6)

- абсолютное демпфирование.

Величины ω_* , k, m могут быть определены экспериментально по полученной временной характеристике (рис.5)-фактически - это экспериментально полученное выражение (16).

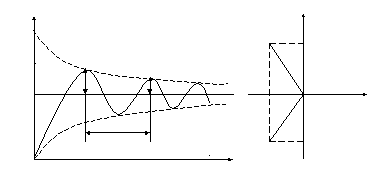
y(t) jIm(p)

-α_*

A1 ω_*

A2 Re(p)

Θ

t

Рис.5

Из рисунка 5 непосредственно видно, что ,

и 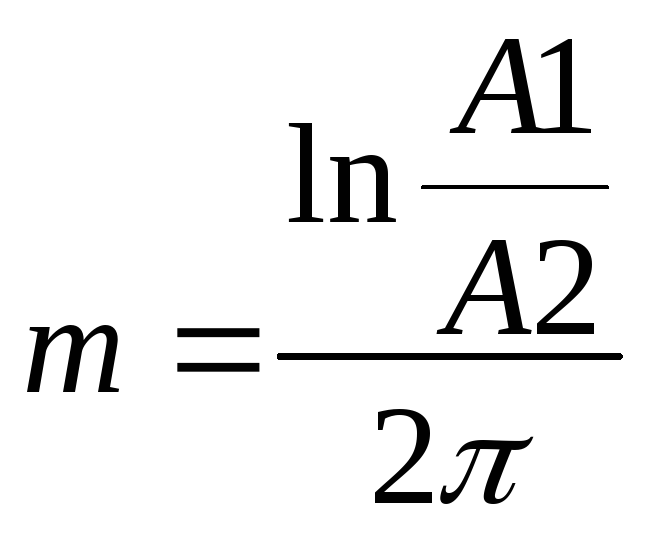, (17)

(18)

Коэффициент k определяется по аналогии с А1- звеном. Из рис.6 можно увидеть, что при m=0 величина α_*=0 и корни p_I,2 находятся на мнимой оси. При этом А1=А2 и временные характеристики не затухают (граница устойчивости).

Если m→∞, то ω_*→0 и корни p_1,2 становятся вещественными и равными, временная характеристика обращается в экспоненту, а К-звено – в апериодическое звено 2-ого порядка. Таким образом, устойчивому колебательному звену отвечают значения m в интервале 0<m<∞, причем, чем больше m, тем меньше колебательность звена.

Применяя к (15) преобразование Лапласа при нулевых начальных условиях имеем:

,

Отсюда получаем:

(19)

Для того чтобы вычислить ξ и T по экспериментальной характеристике, найдем корни характеристического полинома К-звена, т.е. знаменателя W_k(p)

так как ранее эти корни были обозначены:

и ,

то ,.

Тогда из последних равенств можно выразить величины Т, ξ через m, ω_*:

(20)

Подставляя в (19) p=jω, получим частные характеристики К-звена

- АФЧХ (21)

-АЧХ (22)

-ФЧХ (23)

Частотные характеристики К-звена представлены на рис.6.

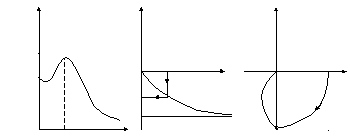W(ω) φ(ω) jIm(ω)

0 ω=1/T ω ω=∞ k ω=0

k Re(ω)

-π/2

-π

ω=1/T ω ω=1/T

Рис.6

Таким образом, по экспериментально снятой временной характеристике К-звена можно определить ω_*, k, m затем ξ и Т.

Используя формулы (21)-(23), построить частотные характеристики К-звена.