
- •5.ЭлЕменты линейной алгебры: системы линейных
- •2.Определители. Базис в пространстве.
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшее
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.ЛинейныЕ операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
4.Аналитическая геометрия в прстранстве: плоскость
и прямая в пространстве; поверхности второго порядка
31. Составить уравнение плоскости, проходящей через точкуМ0 (3,1,-3) параллельную плоскости: 2х-у+5 z-3=0.
32. Составить уравнение плоскости,
проходящей через точку М0(0,-1,2)
и прямую:![]() .
.
33. Составить уравнение плоскости,
проходящей через прямую
![]() перпендикулярно плоскости 3х+у+7z-32=0.
перпендикулярно плоскости 3х+у+7z-32=0.
34. Составить уравнение плоскости, которая проходит через точку М0(-3;0;2)перпендикулярно двум плоскостям:х-2z+3=0, х+3у-z+4=0.
35. Найти расстояние dточкиМ0(2;-1;4) до плоскости4х+7у+4 z+1=0.
36. Найти параметрические уравнения прямой , заданной как линия пересечения двух плоскостей 3х-у-2z+1=0 и х+2у-z+3=0.
37. Даны вершины треугольника А(2;-1;3) В(5;-1;7), С (4;0;5). Составить канонические уравнения биссектрисы его внутреннего угла при вершинеА.
38. Составить каноническое уравнение
прямой, проходящей через точку М0(3;-2;0)параллельной прямой:![]() .
.
39. Найти координаты точки пересечения прямой : х=t, у=2t+1, z=2t+2и плоскости 2х-3у+z-1=0.
40. Найти проекцию точки Р (3;0;4) на
прямую![]() .
.
41. Найти координаты точки Q, симметричной точкеР(3;-1-2) относительно плоскости:х+2у+2z-6=0.
42. Найти координаты точки Qсимметричной точкеР(2;-4;4) относительно
прямой![]() .
.
43. Вычислить расстояниеd
точкиР(-1;0;4)от прямой![]() .
.
44. Составить канонические уравнения
прямой l, которая
проходит через точкуМ0(1;-3;0)и пересекает прямуюl1:![]()
![]() ,l2:
,l2:![]()
![]() используя последовательность действий:
используя последовательность действий:
а) найти координаты нормального вектора
П1(П1х,П1у,П1z),к плоскостиП1проходящей,
через точкуМ0и прямуюl1, взяв
векторное произведение![]() ,
где
,
где![]() (3,-2,-1)
(3,-2,-1)
направляющий вектор прямой l1. М1(2,-1,-1).
точка прямой l1.(см. задачу № 32)
б) найти координаты нормального
вектораП2(П2х,П2у,П2z),к плоскостиП2проходящей,
через точкуМ0и прямуюl2, взяв
векторное произведение![]() ,
где
,
где![]() (2,3,-5)
(2,3,-5)
направляющий вектор прямой l2 М2(5,1,-2).
точка прямой l2.(см. задачу № 32)
в) найти координаты направляющего
вектора
![]() (ах,ау,аz)искомой прямойl, взяв
векторное произведение
(ах,ау,аz)искомой прямойl, взяв
векторное произведение![]() .
.
г) составить канонические уравнения
искомой прямой l,
проходящей через точкуМ0
в направление вектора![]() .
.
45. Даны координаты вершин пирамиды А1(4;7;6), А2(3;7;5), А3(2;5;7), А4(3;3;10).
Найти: 1) угол между ребрами А1А2иА1А4;
2) угол между ребром А1А4; и граньюА1А2А3;
3) уравнение прямой А1А2;
4) уравнение плоскости А1А2А3;
5) уравнение высоты, опущенной из вершины А4на граньА1А2А3.
46. Построить эскиз тела, ограниченного поверхностями:
а) z=4-у2;z=у2+2; х=-1; х=2; б) z= х2+у2+1. Z=0; х=0;у=0; х=4; у=4.
5.Элименты линейной алгебры: системы линейных
уравнений; матрицы; линейное векторное пространство;
линейные операторы
47. Решить систему линейных уравнений методом Гаусса
х1+2х2+3х3+х4=0,
х1+х2+2х3+2х4=0,
2х1+2х2+3х3+х4=0,
48. Найти все вещественные матрицы,
перестановочные с матрицей
![]() .
.
49. Найти матрицу D=3ВА-1+2СВт, где
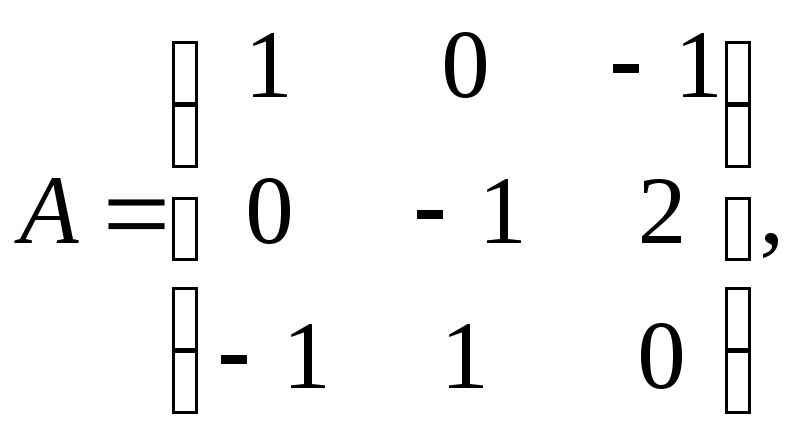


50. Найти ранги матриц: а)
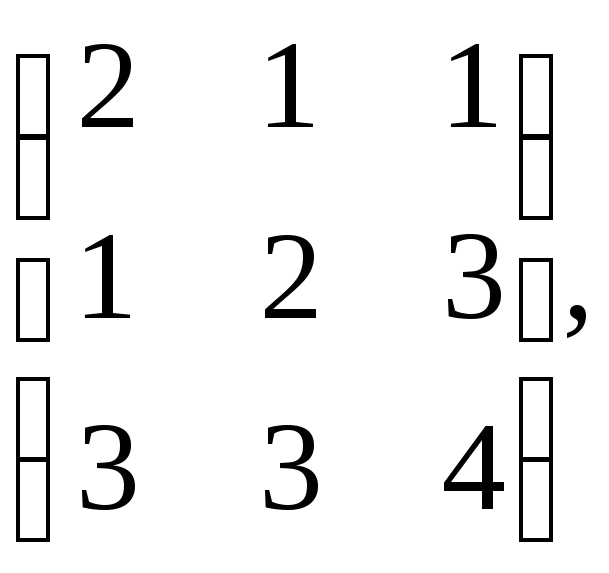 б)
б) .
.
51. Дана система линейных уравнений
х1+х2-х3-=1,
х1-4х2+2х3=-7,
х1-2х2+х3=-4,
Доказать ее совместимость и решить тремя способами:
1) методом Гаусса,
2) средствами метрического исчисления,
по формулам Крамера,
52. Является ли вещественными линейными пространствами:
а) множество всех вещественных матриц
2-го порядка вида
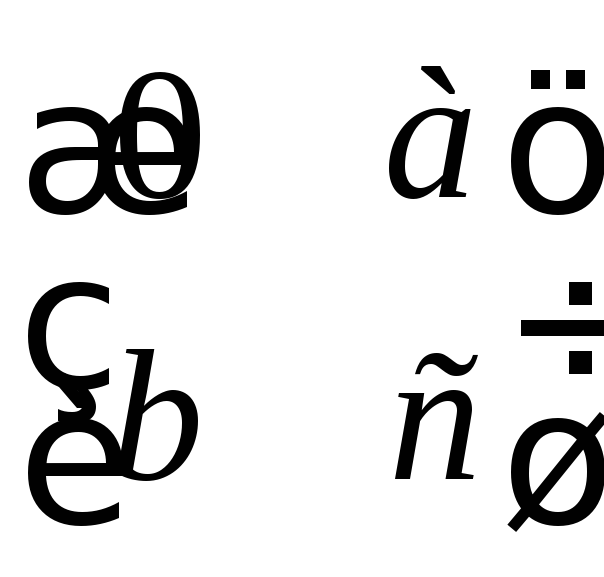 ,
,
б) множество всех вещественных матриц
2-го порядка вида
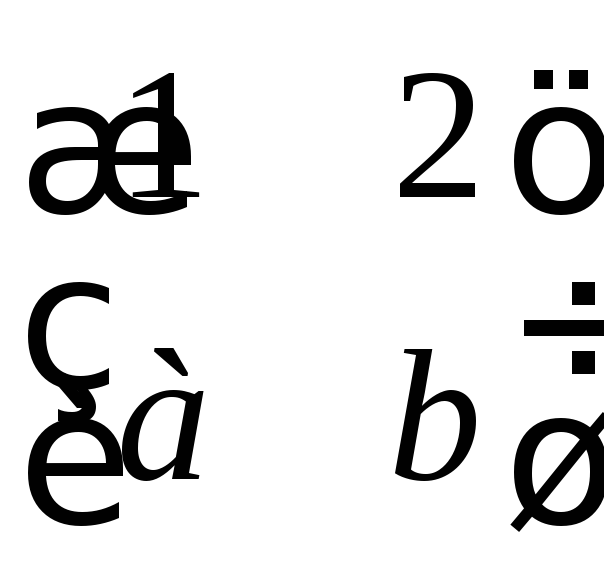 ,
,
53. Найти все значения
![]() ,
при которых вектор
,
при которых вектор![]() линейно выражается через векторы
линейно выражается через векторы![]() ,
если
,
если![]() =(2;1;
=(2;1;![]() );
);![]() =(1;-2;-1);
=(1;-2;-1);
![]() =(2;1;3),
=(2;1;3),
![]() =(3;2;5).
=(3;2;5).
54. Выяснить, является ли данная система векторов из R4 линейно зависимой ?
![]() =(1;2;3;0);
=(1;2;3;0);
![]() =(-1;2;2;-2),
=(-1;2;2;-2),
![]() =(3;-1;0;1),
=(3;-1;0;1),![]() =(4;1;3;1).
=(4;1;3;1).
55. Выяснить геометрический смысл действия
линейных операторов, данных в пространстве
R3, матрицы
которых относительно некоторого
прямоугольного базиса имеют вид: а) б)
б)
56. В пространстве V3задан оператор![]() так:
так:![]()
![]() ,
где
,
где![]() ,
,![]() .
Проверить линейность оператора
.
Проверить линейность оператора![]() и найти его матрицу в базисе (
и найти его матрицу в базисе (![]() ).
).
57. В пространстве
![]() линейный оператор
линейный оператор![]() зеркально отражает векторы относительно
прямой
зеркально отражает векторы относительно
прямой![]() ,
а линейный оператор
,
а линейный оператор![]() ортогонально проецирует векторы на
плоскость
ортогонально проецирует векторы на
плоскость![]() .Найти матрицу оператора
.Найти матрицу оператора![]()
![]() в
базисе (
в
базисе (![]() ).
).
58. Найти собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей

ОТВЕТЫ:
1. 4х+3у-10=0, х+у+3=0, 3х+2у-13=0.2.(3,-3).(2,4),
2х+у-3=0, 2х+у-8=0. 3.х-у=-3, х-у=3, х+у=-3.
4.х-2у-2=0, 3х-у-6=0, (2,0)5.(4;-7) и (5;-5).6.7х-2у-32=0, 5х+у-35=0, 2х-3у-31=0.7.6. 8.5кв. ед.. 9. 1) окружность с центром в полюсе
и радиусом4; 2) луч, выходящий из
полюса, наклоненный к полярной оси под
углом![]() 3)
прямая, перпендикулярная к оси, отсекающая
на ней, считая от полюса, отрезок а=17;
4) прямая расположенная в верхней
полуплоскости, параллельная полярной
оси, отстоящая от нее на расстоянии15;5) окружность с центром С(
3)
прямая, перпендикулярная к оси, отсекающая
на ней, считая от полюса, отрезок а=17;
4) прямая расположенная в верхней
полуплоскости, параллельная полярной
оси, отстоящая от нее на расстоянии15;5) окружность с центром С(![]() ,r=12)
и радиусом12; 6) окружность с центром
С(
,r=12)
и радиусом12; 6) окружность с центром
С(![]() ,r=15) и радиусом15.10.
Эллипс: С(-1;2)
,r=15) и радиусом15.10.
Эллипс: С(-1;2)![]() ,
а=4, в=
,
а=4, в=![]() ,
,![]() .
11.
.
11.![]() .
12. Гипербола:
.
12. Гипербола:![]() .13.
в)парабола:
.13.
в)парабола:![]() .14.
а)2; б)-9; в)-50; г)4.15.
.14.
а)2; б)-9; в)-50; г)4.15.![]() =(2;1;1).16.
=(2;1;1).16.![]() 17.а)
17.а)![]()
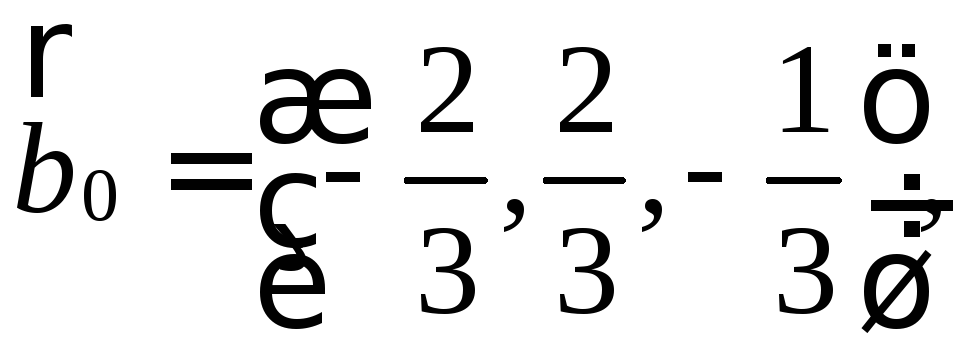
б)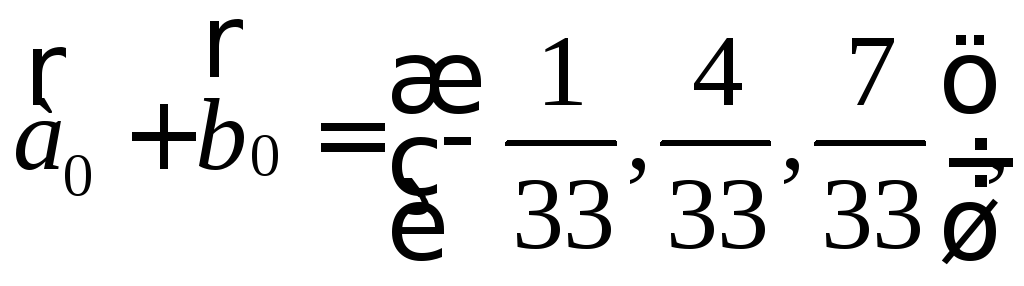 в)
в)![]() (-2,8,14).
18.3. 19. -1. 20.
(-2,8,14).
18.3. 19. -1. 20.![]() =arccos
=arccos
![]() =610031.
21. –56. 22.
=610031.
21. –56. 22.![]() .
23.
.
23.
![]() (3;2;1);
(3;2;1);![]() .
24.S
.
24.S![]() =
=![]() ,h
,h![]() =
=![]() .25.
.25.
![]() .
26. ±16. 27. 5. 28.
.
26. ±16. 27. 5. 28.
![]() левая
тройка векторов. 29.V=22
куб.ед. 30. –30. 31. 2х-у+5z+10=0.
32. 2х+4у-7z+18=0. 33. 3х+у+7z-32=0.
34. 6Х-у+3z+12=0. 35.d=2.
36. Х=5t, у=t+1,z=7t-1. 37.
левая
тройка векторов. 29.V=22
куб.ед. 30. –30. 31. 2х-у+5z+10=0.
32. 2х+4у-7z+18=0. 33. 3х+у+7z-32=0.
34. 6Х-у+3z+12=0. 35.d=2.
36. Х=5t, у=t+1,z=7t-1. 37.![]() .
38.
.
38.![]() .
39. (-1,-1,0). 40.(4,2,6). 41. (5,3,2). 42. (4,0,0). 43=3. 44.
.
39. (-1,-1,0). 40.(4,2,6). 41. (5,3,2). 42. (4,0,0). 43=3. 44.![]() 45. 1)arccos
45. 1)arccos
![]() =1110381.
2)arccos
=1110381.
2)arccos![]()
![]() .
3)
.
3)![]() 4)
-2х+3у+2z-25=0. 5)
4)
-2х+3у+2z-25=0. 5)![]() 47. Х=С
47. Х=С![]() ,
где С
,
где С![]() .
48.
.
48. ,гдеа,а,в
,гдеа,а,в![]() .49.
.49.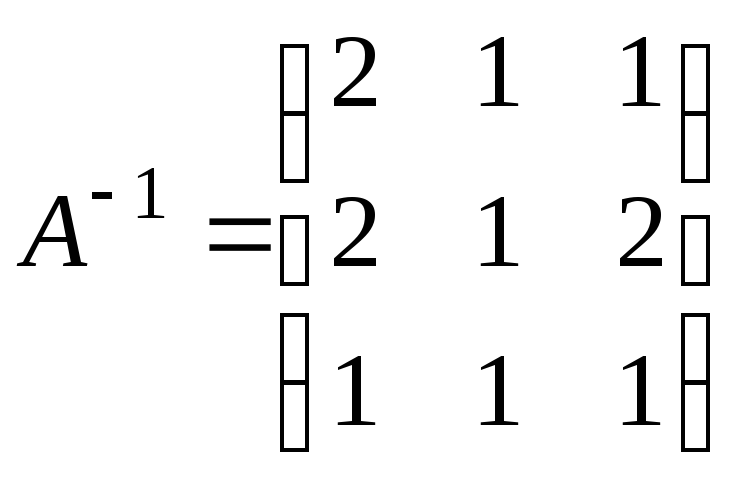

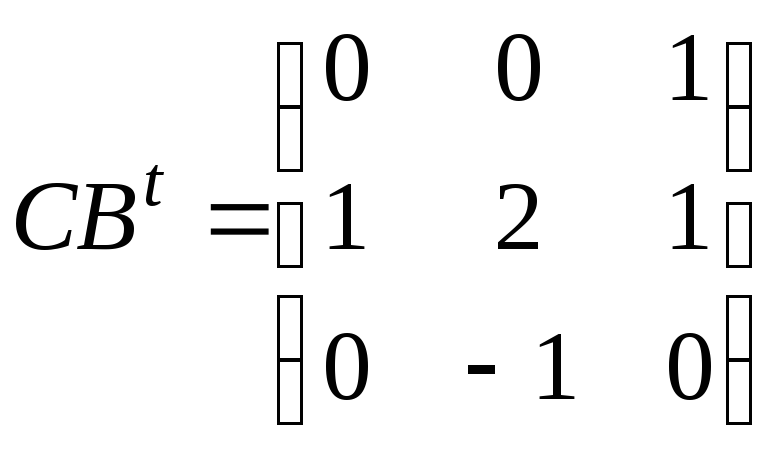 ,
, .
50. а)r=2, б) )r=4.
51. х1=-1, х2=1, х3=-1. 52. а)
да, б) нет.53.
.
50. а)r=2, б) )r=4.
51. х1=-1, х2=1, х3=-1. 52. а)
да, б) нет.53.![]() .54.
да. 55. а)отражение на плоскость относительно
оси Оу, б) поворот трехмерного пространства
на угол 300вокруг оси Оz,
56. Оператор
.54.
да. 55. а)отражение на плоскость относительно
оси Оу, б) поворот трехмерного пространства
на угол 300вокруг оси Оz,
56. Оператор![]() линейный;
линейный; ,
его матрица в базисе (
,
его матрица в базисе (![]() ).57.
А=
).57.
А=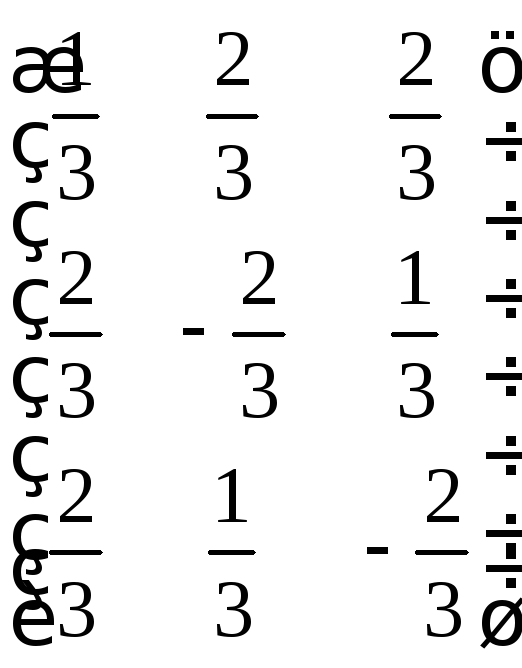 ,
В=
,
В= ,
АВ=
,
АВ=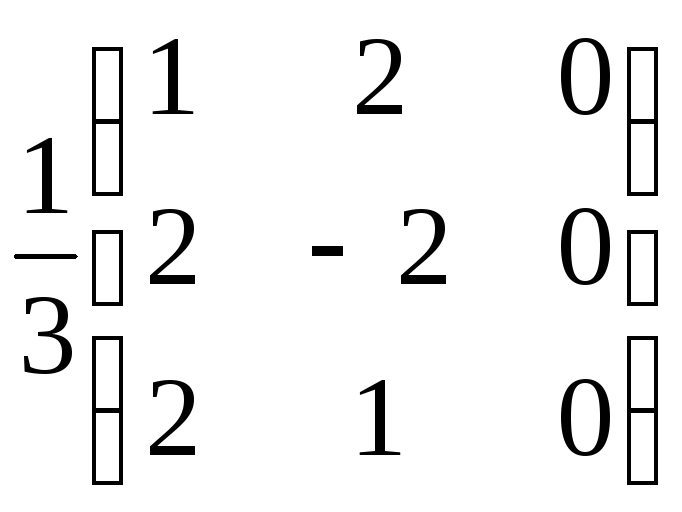 .
58. Собственные значения:
.
58. Собственные значения:![]() =1,
=1,![]() =3,
=3,![]() =-33
Собственные векторы:
=-33
Собственные векторы: ,
,
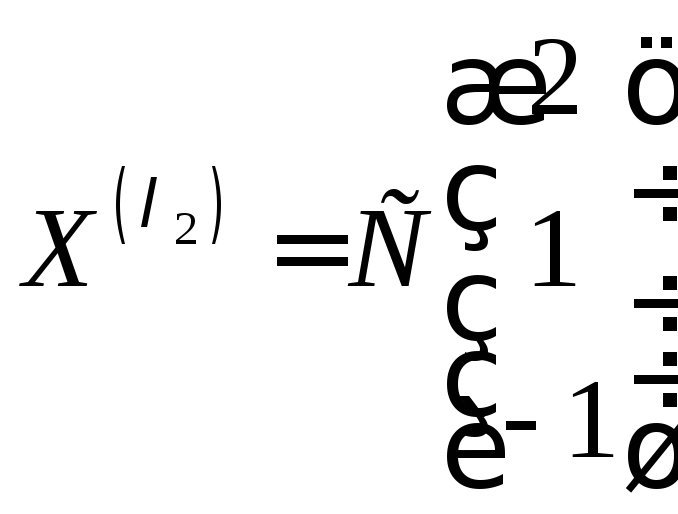 ,
где С
,
где С![]() ,
С
,
С![]() .
.
![]()
ВАРИАНТ 13
