
- •5.ЭлЕменты линейной алгебры: системы линейных
- •2.Определители. Базис в пространстве.
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшее
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.ЛинейныЕ операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
4.Аналитическая геометрия в прстранстве: плоскость
и прямая в пространстве; поверхности второго порядка
31. Составить уравнение плоскости, проходящей через точкуМ (2,-1,-1) параллельную плоскости:3х+у- z+2=0.
32. Составить уравнение плоскости,
проходящей через две параллельные
прямые:
![]() .
.
33. Составить уравнение плоскости,
проходящей через прямую
![]() перпендикулярно плоскостих+у-2z+3=0.
перпендикулярно плоскостих+у-2z+3=0.
34. Составить уравнение плоскости, которая проходит через точку А(2;-3;1)перпендикулярно двум плоскостям:х-у+2=0, 3х+2у+-z+5=0.
35. Найти расстояние dточкиМ(-1;5;7) до плоскости2х-у+2 z-1=0.
36. На оси Охнайти координаты точек, отстоящих от плоскости4х-7у+4z+2=0 на расстоянииd=2.
37. Даны вершины треугольника А(1;2;3) В(-1;3;1), С (-7;6;-1). Составить канонические уравнения биссектрисы его внутреннего угла при вершинеВ.
38. Составить каноническое уравнение прямой, проходящей через точку
М(-1;3;-2)параллельной прямой:х=5t-2, у=2 t+4, z= t-3.
39. Найти координаты точки пересечения
прямой
![]() и плоскостих-3у+2z+1=0.
и плоскостих-3у+2z+1=0.
40. Найти проекцию точки М (-1;-3;0) на прямуюх=t, у=-2t+5, z=5t-3.
41. Найти координаты точки М1, симметричной точкеМ2(-1;5;2) относительно плоскости:2х-у+2z+12=0.
42. Найти координаты точки М1,
симметричной точкеМ2(0;4;3)
относительно прямой:![]() .
.
43. Вычислить расстояниеd
точкиМ(3;-1;3)от прямой![]() .
.
44. Составить канонические уравнения
прямой, которая проходит через точку
М0(8;3;1)параллельно
плоскости П:3х-2у-3z+3=0и пересекает прямуюl:![]()
![]() ,
используя последовательность действий:
,
используя последовательность действий:
а) найти уравнение плоскости П1,проходящей через точкуМ0параллельно плоскостиП(см. задачу 31);
б) найти координаты точки М1пересечения прямойlи плоскостиП1(см. задачу 39);
в) найти канонические уравнения искомой прямой, как прямой, проходящей через точки М0 и М1.
45. Даны координаты вершин пирамиды А1(5;2;-1), А2(4;1;-1), А3(1;-2;-2), А4(2;2;6).
Найти: 1) угол между ребрами А1А2иА1А4;
2) угол между ребром А1А4; и граньюА1А2А3;
3) уравнение прямой А1А2;
4) уравнение плоскости А1А2А3;
5) уравнение высоты, опущенной из вершины А4на граньА1А2А3.
46. Построить эскиз тела, ограниченного поверхностями:
а) z=0; z=х2; 2х-у=0; х+у=9;
б) z2=4-у; х2+у2=4у.
5.Элементы линейной алгебры: системы линейных
уравнений; матрицы; линейное векторное пространство;
линейные операторы
47. Решить систему линейных уравнений методом Гаусса
х1+х2-2х3-х4=0,
х1+2х2+х3-2х4=0,
2х1+3х2+3х3-3х4=0,
48. Найти все вещественные матрицы,
перестановочные с матрицей
![]() .
.
49. Найти матрицу D=3А-1С-ВСт, где

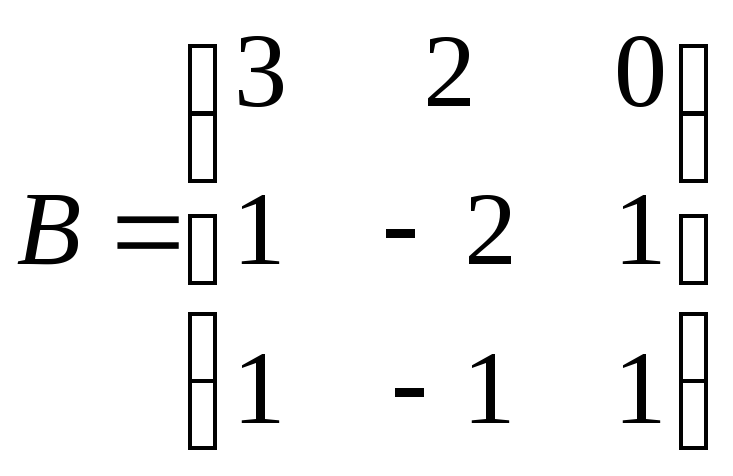 ,
,
50. Найти ранги матриц: а)
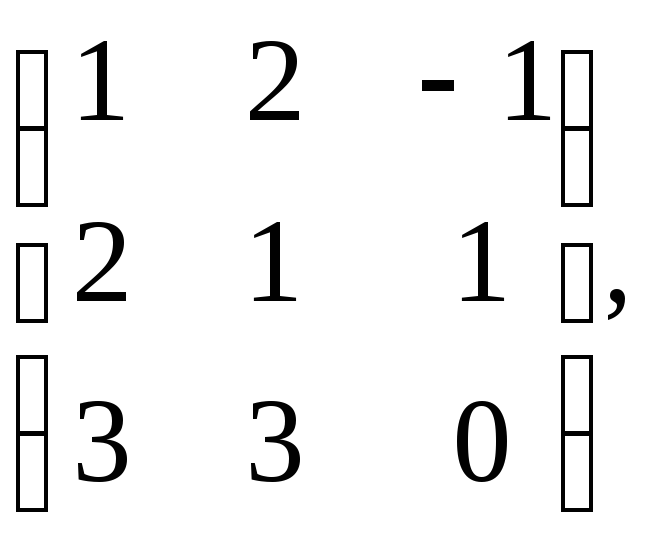 б)
б) .
.
51. Дана система линейных уравнений
х1+9х2-4х3=5,
2х1-8х2+5х3=-3,
4х1-3х2+2х3=8,
Доказать ее совместимость и решить тремя способами:
1) методом Гаусса,
2) средствами матричного исчисления,
по формулам Крамера,
52. Являются ли вещественными линейными пространствами:
а) все векторы (х;у;z)арифметического пространстваR3,координаты которых удовлетворяют уравнениюх-3у+5z=0,
б) все векторы (х;у;z)изR3,, координаты которых удовлетворяют уравнению
х-3у+5z=2.
53. Найти все значения
![]() ,
при которых вектор
,
при которых вектор![]()
![]() линейно выражается через векторы
линейно выражается через векторы![]() ,
если =(1;2;
,
если =(1;2;![]() );
);![]() =(1;2;3);
=(1;2;3);
![]() =(2;-1;1),
=(2;-1;1),
![]() =(-1;1;0).
=(-1;1;0).
54. Выяснить, является ли данная система векторов из R 4 линейно зависимой ?
![]() =(2;1;0;1);
=(2;1;0;1);
![]() =(1;2;1;-1),
=(1;2;1;-1),
![]() =(1;0;0;-2),
=(1;0;0;-2),![]() =(3;1;0;-1).
=(3;1;0;-1).
55. Выяснить геометрический смысл действия
линейных операторов, данных в пространстве
R3, матрицы
которых относительно некоторого
прямоугольного базиса имеют вид: а) б)
б)
56. Показать, что дифференцирование является линейным преобразованием пространства всех многочленов степени ≤4 от одного неизвестного с вещественными коэффициентами и найти матрицу этого преобразования в базисе:f1(х)=1, f2(х)=х, f3(х)=х2, f4(х)=х3, f5(х)=х4.
57. Линейный оператор
![]() - оператор зеркального отражения векторов
плоскости относительно прямойу=-3х,
а оператор
- оператор зеркального отражения векторов
плоскости относительно прямойу=-3х,
а оператор![]() - оператор поворота плоскости вокруг
начала координат на угол
- оператор поворота плоскости вокруг
начала координат на угол![]() .
Найти матрицы операторов
.
Найти матрицы операторов![]() ;
;![]() ;
;![]()
![]() в базисе(
в базисе(![]() .
.
58. Найти собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей

ОТВЕТЫ:
2. 4х+у+10=0. 3.(-7;0). 4.(2;-2) и (-2,-4).
5.(-2;-5) и (-3;-4).6.2х-5у+4=0, 2х-5у-25=0,
7х-3у-15=0.7.х+2у+5=0, х-1=0, х-4у+11=0. 8.d=![]() .9. 1) окружность с центром в полюсе и
радиусом 1; 2) луч, выходящий из полюса,
наклоненный к полярной оси под углом
.9. 1) окружность с центром в полюсе и
радиусом 1; 2) луч, выходящий из полюса,
наклоненный к полярной оси под углом![]() ;
3) прямая, перпендикулярная к оси,
отсекающая на ней, считая от полюса,
отрезока=3; 4) прямая расположенная
в верхней полуплоскости, параллельная
полярной оси, отстоящая от нее на
расстоянии 5; 5) окружность с центромС(
;
3) прямая, перпендикулярная к оси,
отсекающая на ней, считая от полюса,
отрезока=3; 4) прямая расположенная
в верхней полуплоскости, параллельная
полярной оси, отстоящая от нее на
расстоянии 5; 5) окружность с центромС(![]() ,r=2)
и радиусом 2; 6) окружность с центром С(
,r=2)
и радиусом 2; 6) окружность с центром С(![]() ,r=1) и радиусом 1. 10.
Гипербола:
,r=1) и радиусом 1. 10.
Гипербола:
![]() ,
С(1;-2),полуосиа=
,
С(1;-2),полуосиа=![]() ,
,![]() =
=![]() ,
,![]() .11.
.11.
![]() .
12. Парабола:(у+1)2=8(х-5).13. в) левая ветвь гиперболы:
.
12. Парабола:(у+1)2=8(х-5).13. в) левая ветвь гиперболы:
 .
14. а) -7; б) –12; в) 6; г) 2. 15.
.
14. а) -7; б) –12; в) 6; г) 2. 15.![]()
![]() =(2;-1;-3).16.
=(2;-1;-3).16.![]() 17.а)
17.а)![]()
 б)
б)
в)![]() (10,2,-20).
18.
(10,2,-20).
18.
![]() .19.–3. 20. arccos
.19.–3. 20. arccos
![]() =1000.
21. ±(6;4;0).22.
=1000.
21. ±(6;4;0).22.
![]() .23.
.23.
![]() (-1;5;2);
(-1;5;2);![]() .
24.S
.
24.S![]() =
=![]() ,h
,h![]() =
=![]() .25.
±1.26.
.25.
±1.26.
![]() =(-6;6;0).27.-11.28. Компланарны. 29.V=8
куб.ед. 30.–18. 31.3х+у-z-6=0.32.2х+5у+4z+19=0.
=(-6;6;0).27.-11.28. Компланарны. 29.V=8
куб.ед. 30.–18. 31.3х+у-z-6=0.32.2х+5у+4z+19=0.
33. 9х-7у+z-28=0.34.х+у+5z-4=0. 35.d=2.36.(4;0;0) и
(-5;0;0). 37.![]() .
38.
.
38.![]() .
39.(11,6,3). 40.(1,3,2).41.(-5,7,-2).42.(-6,10,-3).43. d=3.
44.
.
39.(11,6,3). 40.(1,3,2).41.(-5,7,-2).42.(-6,10,-3).43. d=3.
44.![]() 45. 1)arccos
45. 1)arccos![]() .2)arccos
.2)arccos![]() -
-![]() .
3)
.
3)
![]() 4)х-у+1=0.5)
4)х-у+1=0.5)
![]() 47.Х=
47.Х=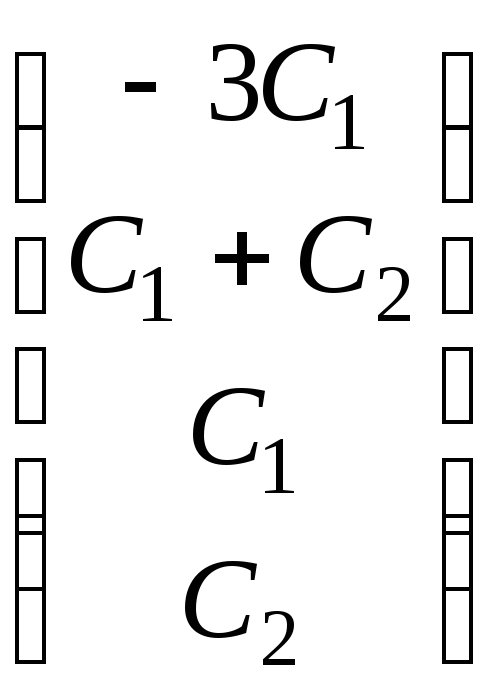 ,
гдеС1,С2
,
гдеС1,С2![]() .48.
.48. ,
гдеа,в
,
гдеа,в![]() .49.
.49. ,
,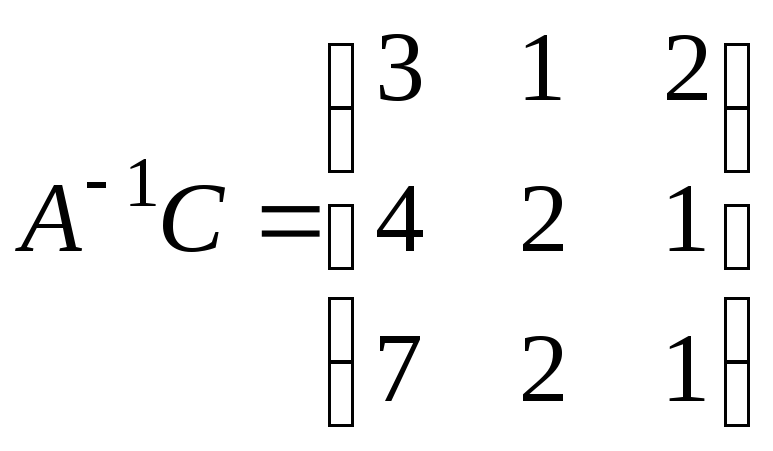 ,
,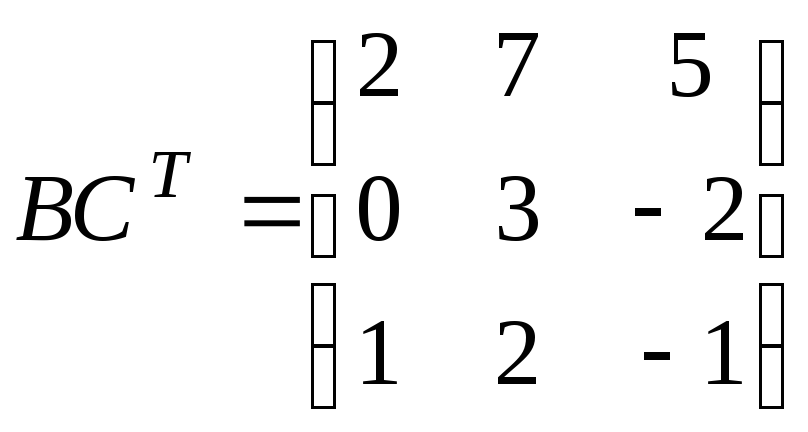 ,
, .
50.а) r=2, б) ) r=3.
51.х1=3, х2=-2,
х3=-5. 52. а) да, б) нет. 53.
.
50.а) r=2, б) ) r=3.
51.х1=3, х2=-2,
х3=-5. 52. а) да, б) нет. 53.
![]() .54. да. 55. а) проектирование на
плоскость
.54. да. 55. а) проектирование на
плоскость![]() б)
проектирование на плоскость
б)
проектирование на плоскость![]() с
последующим относительно начала
координат. 56.
с
последующим относительно начала
координат. 56. .
57. А=
.
57. А=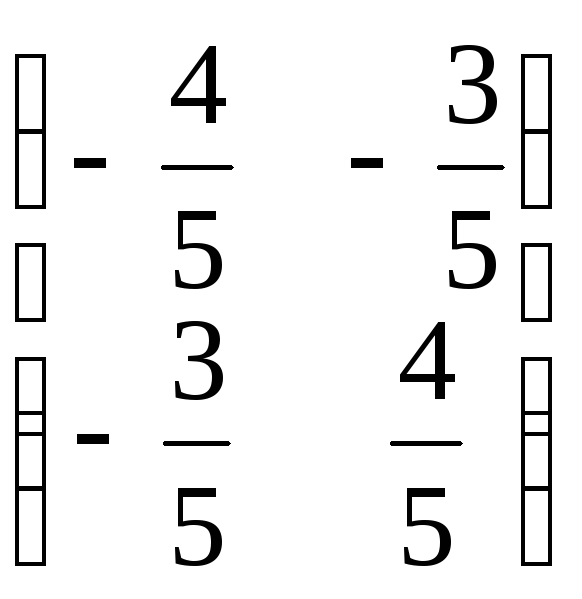 ,
В=
,
В=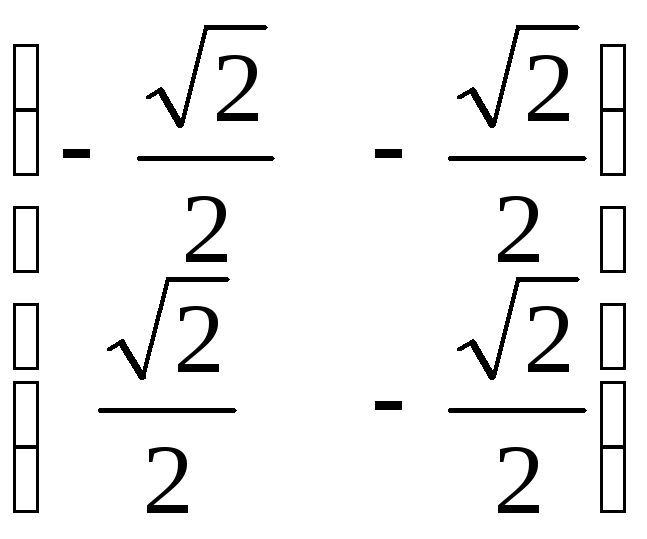 ,
АВ=
,
АВ=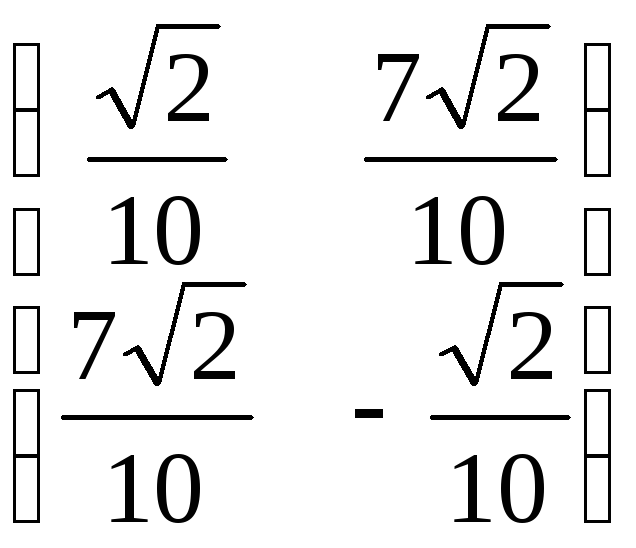 .
58. Собственные значения:
.
58. Собственные значения:![]() =0,
=0,![]() =6,
=6,![]() =3.
Собственные векторы:
=3.
Собственные векторы: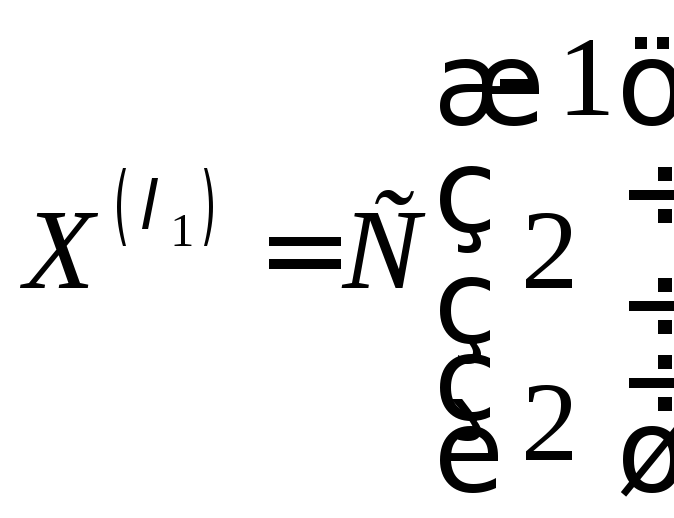 ,
, ,
,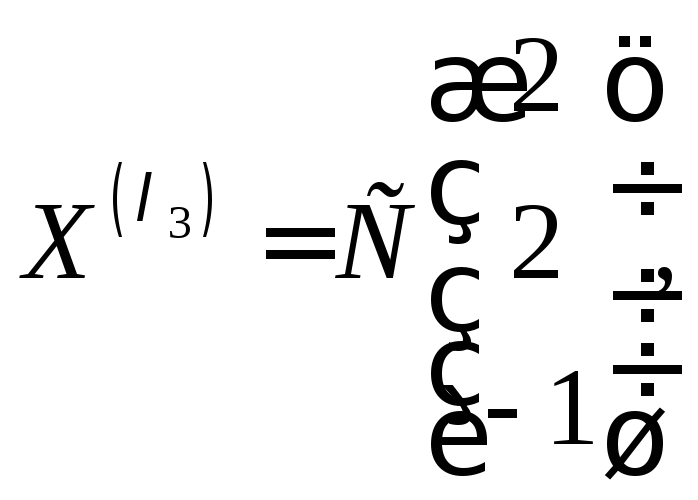 С
С![]() ,
,![]() .
.
![]()
ВАРИАНТ 11
