
- •5.ЭлЕменты линейной алгебры: системы линейных
- •2.Определители. Базис в пространстве.
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшее
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.ЛинейныЕ операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.Элименты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
- •1.Аналитическая геометрия на плоскости: простейшИе
- •2.Определители. Базис в пространстве.
- •3.Линейны операции над векторами, проекция вектора
- •4.Аналитическая геометрия в прстранстве: плоскость
- •5.ЭлЕменты линейной алгебры: системы линейных
1.Аналитическая геометрия на плоскости: простейшее
задачи аналитической геометрии на плоскости; прямая
на плоскости; линии второго порядка на плоскости.
Доказать, что точки А (-1,1), В (-4,5), С (-8,2) и D (-5,-2)являются вершинами квадрата.
Даны вершины треугольника А (-2,-2), В (-5,0), С (0,4). Составить уравнение перпендикуляра, опущенного из вершиныАна медиану, проведенную из вершиныВ.
Найти координаты точки М, симметричной точкеМ2 (3,2)относительно прямой , проходящей через точкиА (-2,1), В (-1,-4).
Даны две смежные вершины параллелограмма А (-6,2), В (-2,4)и точка пересечения его диагоналейМ (-2,0).Определить координаты двух других вершин.
Отрезок, ограниченный точками А (-1,-6), В (-4,-3), разделен на три равные части. Определить координаты точек деления.
Даны уравнения двух сторон прямоугольника 5х+2у+10=0, 5х+2у-19=0и уравнение его диагонали3х+7у+6=0.Составить уравнение остальных сторон и второй диагонали этого прямоугольника.
Даны две вершины А (-7,1) и В (1,-3) и точкаД (0,1) пересечения высот треугольника. Составить уравнение его сторон.
Найти расстояние от точки М (-7,1)до прямой, проходящей через точки
А (-4,1)иВ (-2,5).
Установить, какие линии определяются в полярных координатах следующими уравнениями ( построить их на чертеже):
![]() 2)
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]() ,
5)
,
5)![]() ,
6)
,
6)![]() .
.
Установить, какая линия определяется уравнением 3х2-7у2-6х-28у-46=0. Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.
Точка М1(4,-2) является концом малой оси эллипса, фокусы которого лежат на прямойу+4=0. Составить уравнение этого эллипса, зная его эксцентриситет ε=
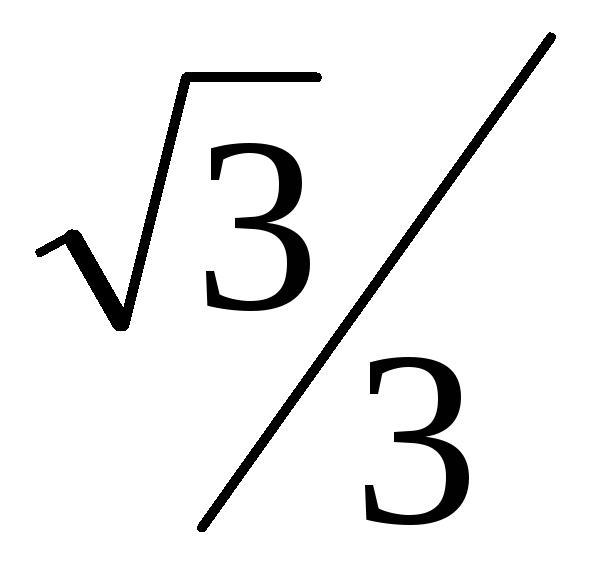 .
.Составить уравнение линии, каждая точка которой равноудалена от точки А (7,-1)и от прямойх-3=0.Определить какая это линия, сделать чертеж.
Линия задана уравнением
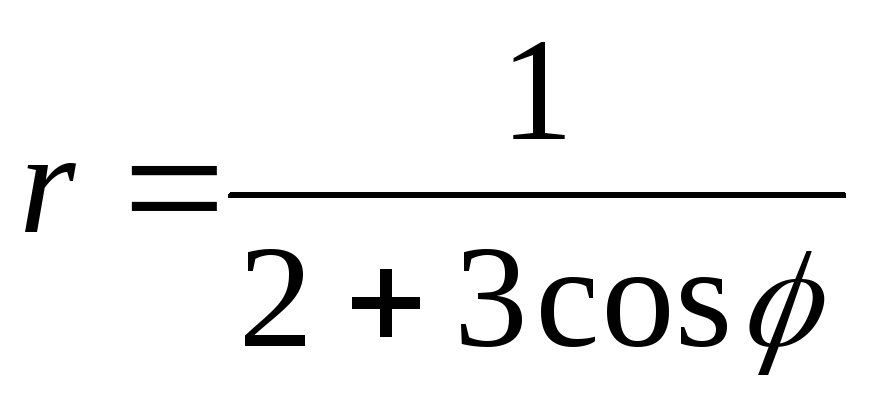 в полярной системе координат. Требуется:
а) построить линию по точкам, начиная
от
в полярной системе координат. Требуется:
а) построить линию по точкам, начиная
от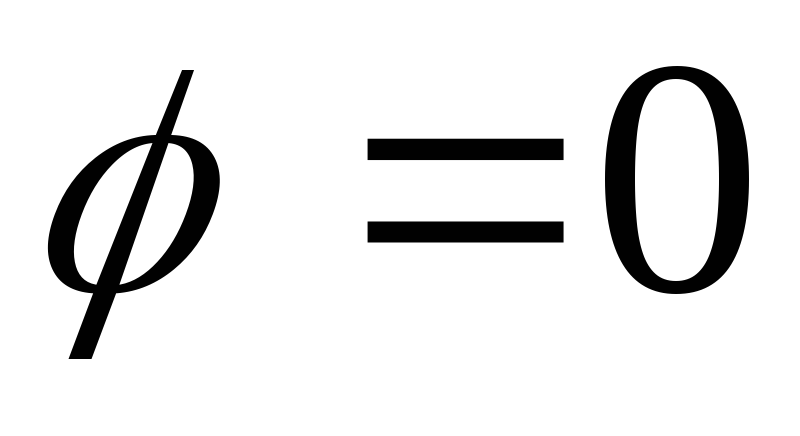 до
до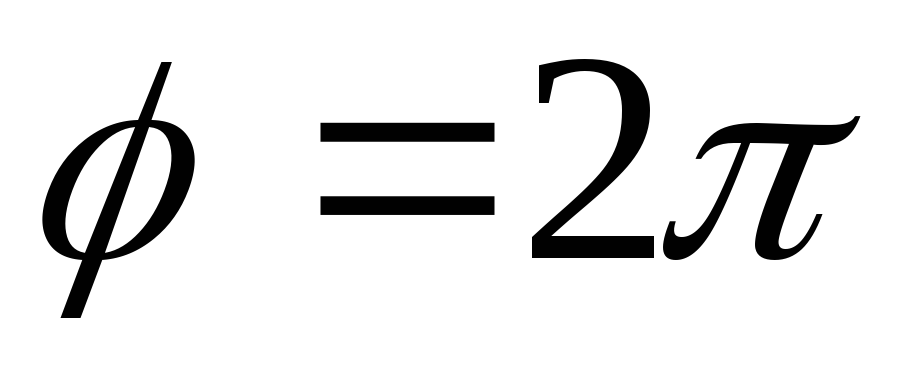 придавая
придавая значения через промежуток
значения через промежуток ;
;
б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
в) по полученному уравнению определить, какая это линия .
2.Определители. Базис в пространстве.
координаты вектора.
Вычислить определители:
а) по правилу треугольника;
б) разложением по элементам первой строки;
в) разложением по элементам второго столбца;
г) сведением к треугольному виду:
а) ;
б)
;
б)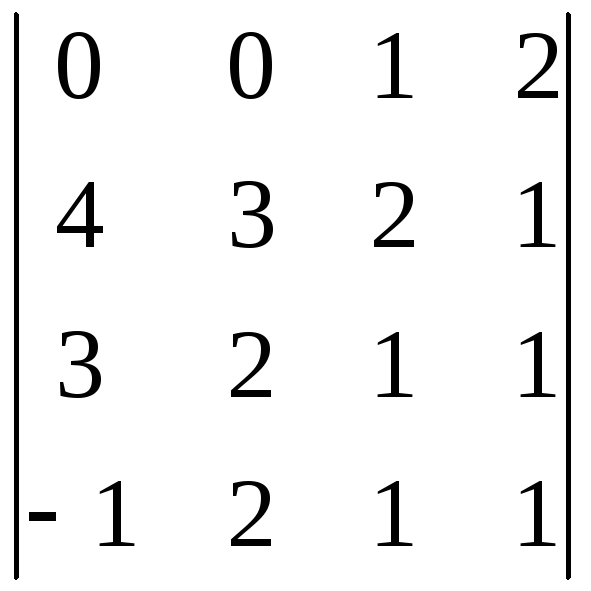 ;
в)
;
в)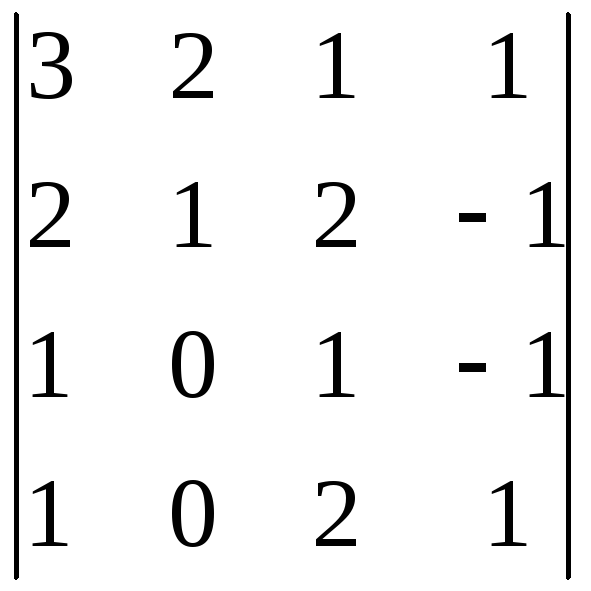 ;г)
;г)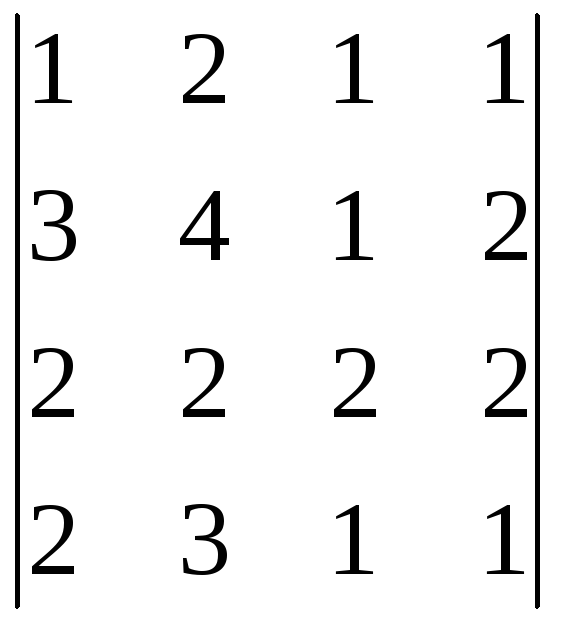 .
.
Даны векторы:
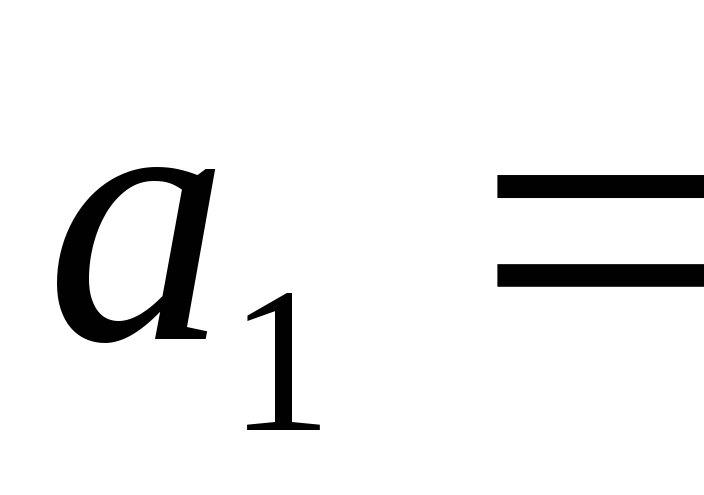 (1,2,-1),
(1,2,-1), =(0,-3,1),
=(0,-3,1), =(2,1,0),
=(2,1,0),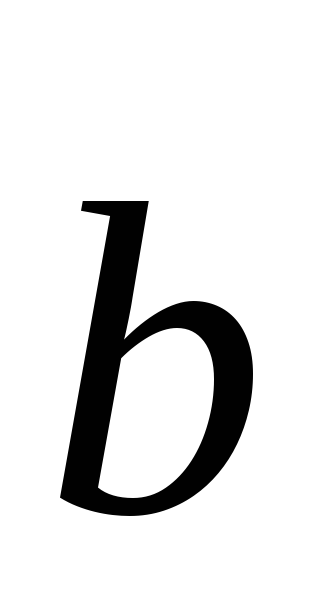 =(-4,4,-3)в некотором базисе. Показать, что первые
три вектора сами образуют базис и найти
координаты векторов
=(-4,4,-3)в некотором базисе. Показать, что первые
три вектора сами образуют базис и найти
координаты векторов
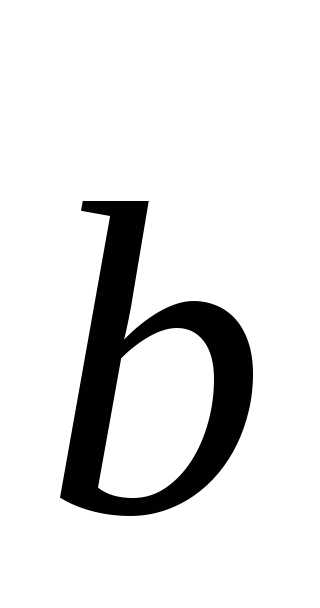 в этом базисе.
в этом базисе.
3.Линейны операции над векторами, проекция вектора
на ось, скалярное, векторное и смешаные произведения
векторов
Найти координаты единичного вектора (орта)
 ,
сонаправленного с вектором
,
сонаправленного с вектором =
(1,1,-3).
=
(1,1,-3).Два вектора
 =(6,-3,2)
и
=(6,-3,2)
и  =(-7,4,-4)
приложены к одной точке. Найти
координаты:
=(-7,4,-4)
приложены к одной точке. Найти
координаты:
а) ортов
![]() и
и![]() векторов
векторов![]() и
и![]() ;
;
б) вектора
![]() +
+![]() ;
;
в) вектора
![]() ,
направленного по биссектрисе угла между
векторами
,
направленного по биссектрисе угла между
векторами![]() и
и![]() при условии, что
при условии, что![]() =6
=6![]() .
.
Найти проекцию вектора
 =(3,2,5)на направление вектора
=(3,2,5)на направление вектора =2i-2j+3k.
=2i-2j+3k.Найти проекцию вектора
 =(3;-1;-4
=(3;-1;-4 )на ось, составляющую с координатными
осямиОх и Оу углы
)на ось, составляющую с координатными
осямиОх и Оу углы ,
а с осьюОу –острый угол
,
а с осьюОу –острый угол .
.В четырехугольнике ОАВСугол при вершинеОимеет величину 600, а диагональОВявляется биссектрисой этого угла. Известно, что
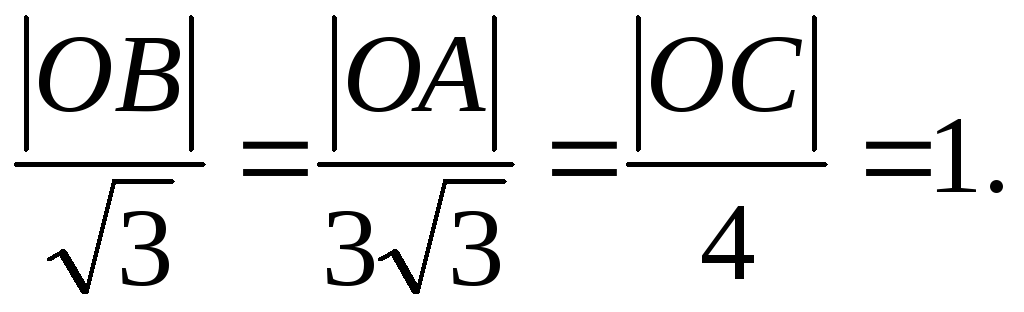 Найти величину угла между векторами
Найти величину угла между векторами и
и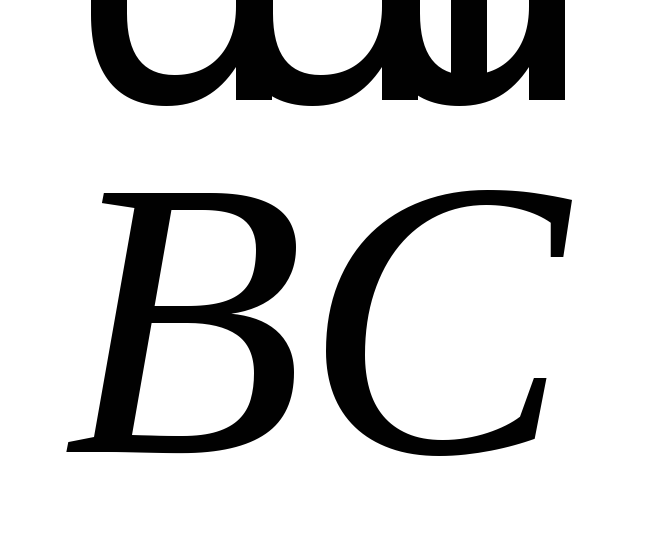 ,
используя последовательность действий:
,
используя последовательность действий:
а) ввести декартову прямоугольную
систему координат
![]() с
началом в точкеОтак, чтобы осьОхбыла направлена по сторонеОСчетырехугольника (в связи с этим сторонуОСжелательно расположить на рисунке
горизонтально);
с
началом в точкеОтак, чтобы осьОхбыла направлена по сторонеОСчетырехугольника (в связи с этим сторонуОСжелательно расположить на рисунке
горизонтально);
б) найти в этой системе координаты точек А,В,С;
в) найти координаты векторов
![]() и
и![]() ;
;
г) найти
![]() по формуле
по формуле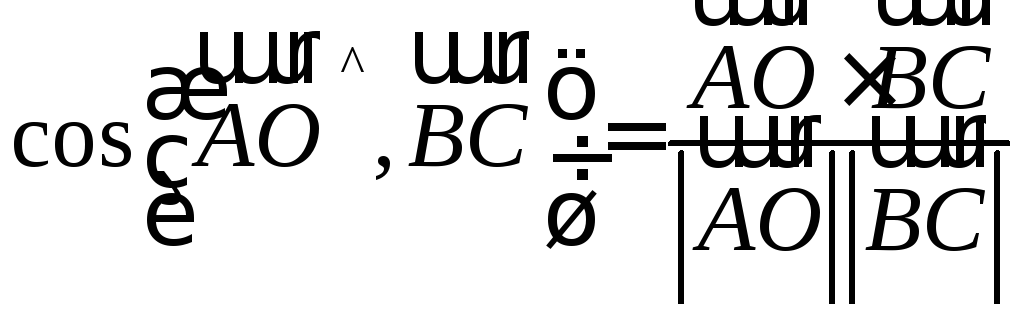
д) подсчитать искомый угол по формуле
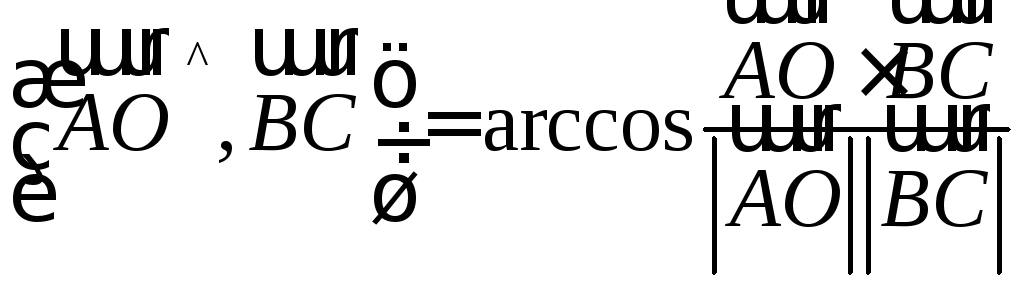
В плоскости ХОУ найти вектор
 ,
перпендикулярный вектору
,
перпендикулярный вектору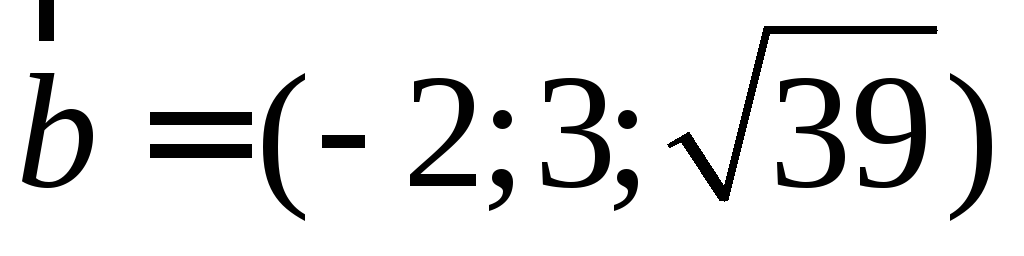
 и
имеющий одинаковую с ним длину.
и
имеющий одинаковую с ним длину.На векторах
 и
и построен треугольник. Найти длину
медианы, проведенной из вершины А, если
построен треугольник. Найти длину
медианы, проведенной из вершины А, если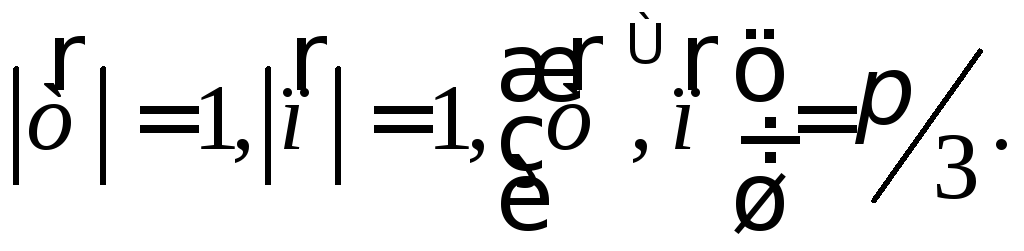
Вычислить координаты векторного произведения
 и его длину
и его длину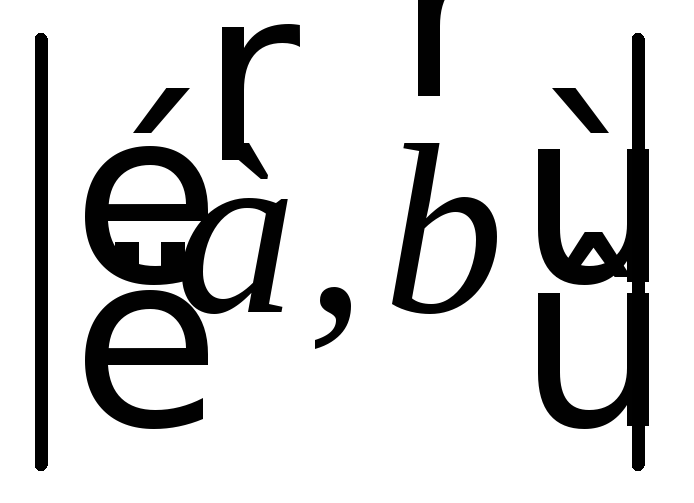 ,
если
,
если
 =(2;0;1),
=(2;0;1), =
= .
.Даны вершины треугольника АВС:А(7;5;3), В(9;6;2), С(3;8;-1). Найти площадь треугольника и длину высоты, опущенной из вершиныА.
25. Вычислить
![]() ,
если
,
если
![]() =1,
=1,![]() =2,
=2,![]() =
=![]() .
.
26. Найти вектор
![]() ,
ортогональный векторам
,
ортогональный векторам![]() =
=![]() ;
;![]() =
=![]() ,
если
,
если![]() 2
гдес=(1;2;-2).
2
гдес=(1;2;-2).
27. Вычислить смешанное произведение
векторов
![]() =(2;-1;-1),
=(2;-1;-1),![]() =(1;0;3),
=(1;0;3),
![]() =(2;1;2).
=(2;1;2).
28. Установить, компланарны ли векторы
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
.
29. Вычислить объем пирамиды, вершины которой: А (2;4;4), В (10;8;5), С (4;2;5), D (6;4;7).
30. Вектор
![]() перпендикулярен к векторам
перпендикулярен к векторам![]() и
и![]() ;
;![]() .
Зная, что
.
Зная, что
![]() =2,
=2,![]() =3
=3![]() ,
,
![]() =3,
найти
=3,
найти![]()
![]()
![]() ,
если тройка векторов
,
если тройка векторов![]() ,
,![]() ,
,![]() - правая.
- правая.
