Электротехника 50 вариант

Вариант 50

Задача 1

Для электрической цепи, показанной на рис. 1.1 – 1.10, составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа, определить токи во всех ветвях, пользуясь любым известным методом расчета электрических цепей постоянного тока. Правильность решения задачи проверить, составив уравнение баланса мощности. Исходные данные приведены в табл. 1.

№ Варианта	Рис.	E1, B	E2, B	E3, B	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
50	1.10	17	39	31	11	11	12	1	16	17

1.10

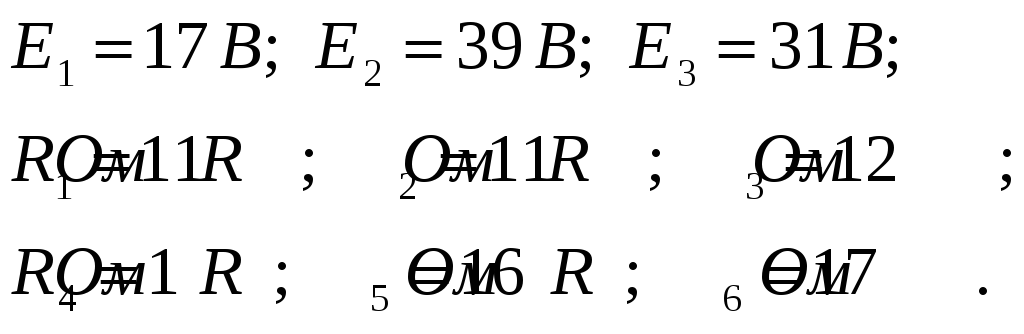
Решение.

1. Составление системы уравнений по законам Кирхгофа.

Выберем направления токов в ветвях и направления обхода контуров.

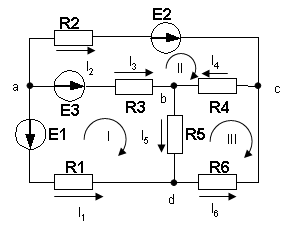
В схеме 4 узла и 3 независимых контура, 6 ветвей. Составляем 4-1=3 уравнения по 1-му закону Кирхгофа и 6-3=3 уравнения по второму закону.

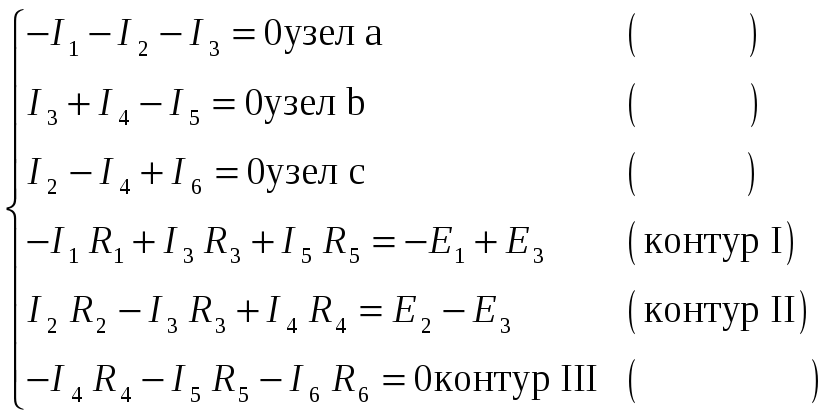
2. Определение токов в ветвях методом контурных токов.

Система уравнений по методу контурных токов в общем виде:

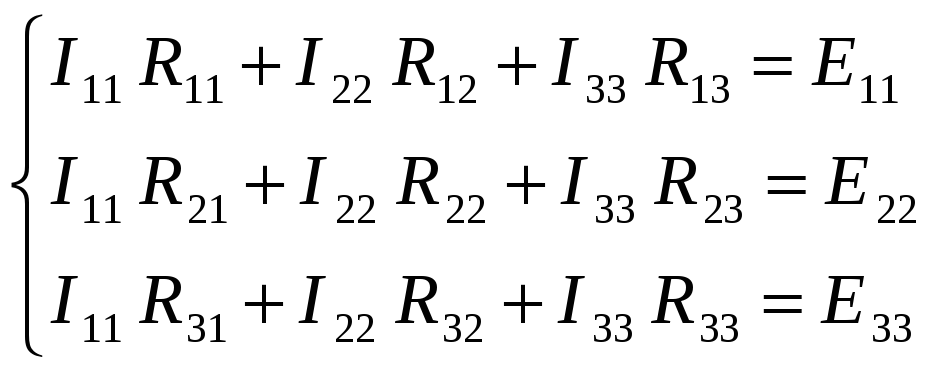
Контурные сопротивления:

Взаимные сопротивления контуров:

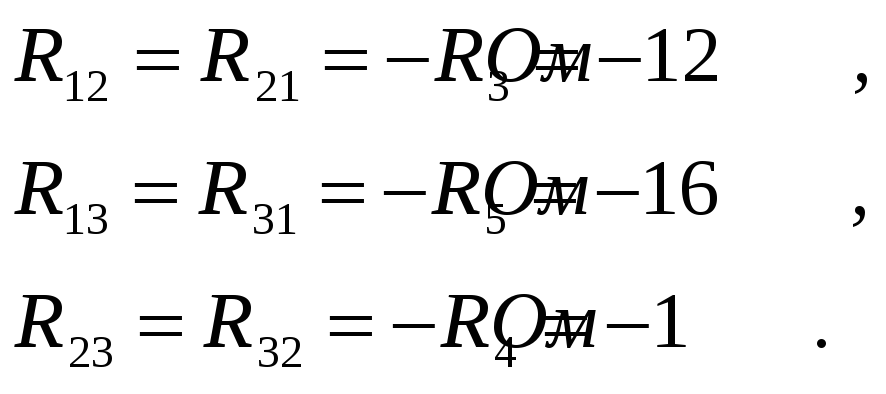
Контурные ЭДС:

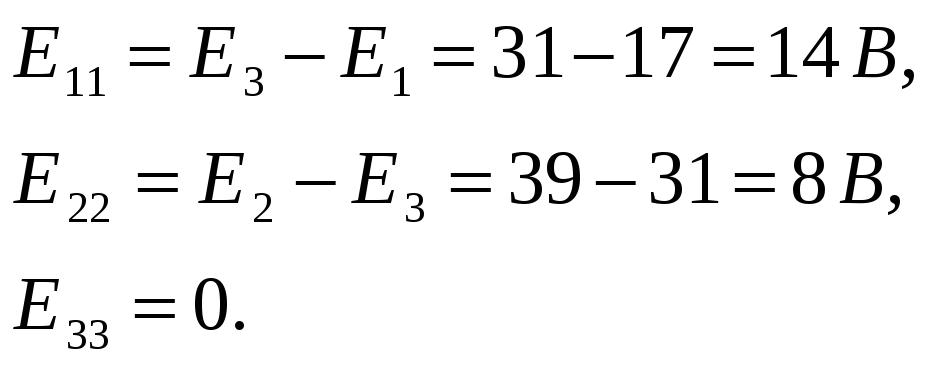
Подставим в систему:

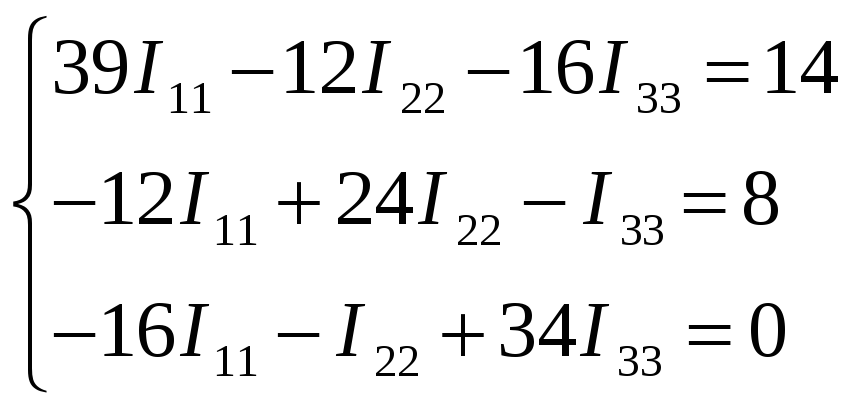
Решим систему методом Крамера.

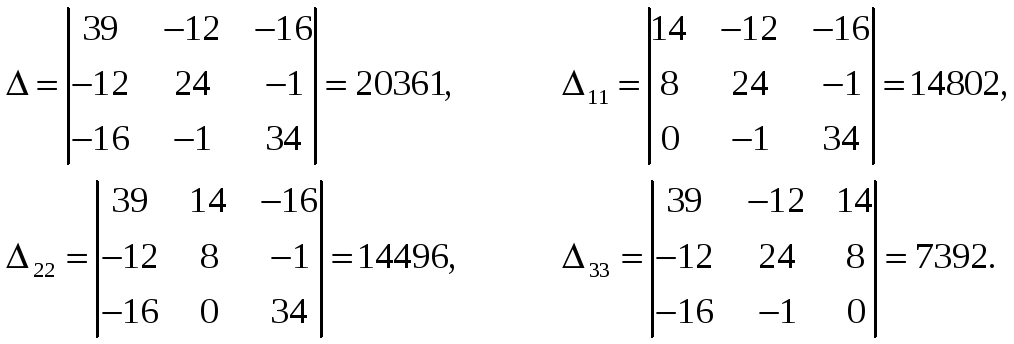
Контурные токи:

Токи в ветвях:

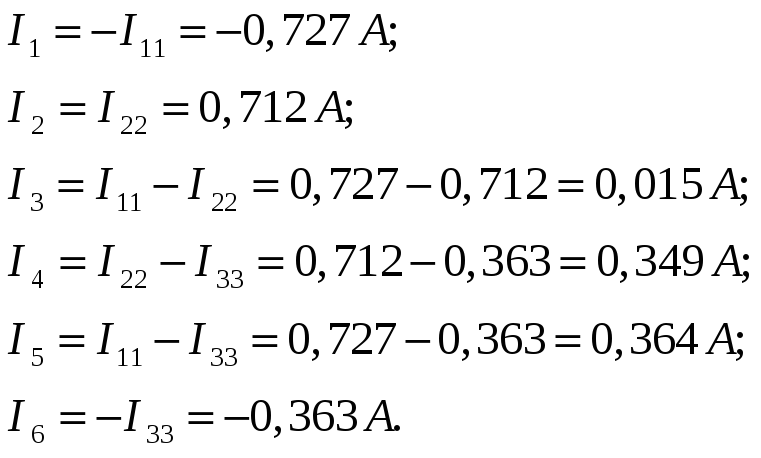
Знаки "-" показывают, что токи I₁ и I₆ направлены противоположно показанному на рисунке.

3. Баланс мощности.

Мощность источников ЭДС

.

Мощность, потребляемая в цепи

.

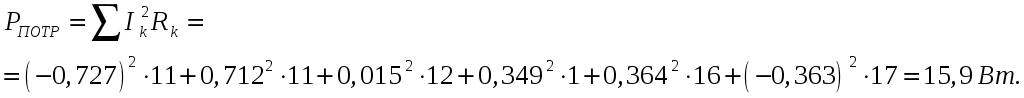
Баланс мощности в цепи соблюдается. Токи определены правильно.

Задача 2

На рис. 2.1 – 2.10 представлена сложная электрическая цепь однофазного синусоидального тока. Частота питающей сети 50 Гц. Параметры цепи указанны в табл. 2. Определить токи, напряжения, мощности на всех участках цепи. Построить в масштабе векторные диаграммы токов и напряжений. Правильность решения проверить, составив уравнения баланса активной, реактивной, полной мощностей.

№ Варианта	Рис.	E, B	R1, Ом	R2, Ом	R3, Ом	C1, мкФ	C2, мкФ	C3, мкФ	L1, мГн	L2, мГн	L3, мГн
50	2.10	175	—	133	—	42.60	24.78	—	—	—	617

2.10

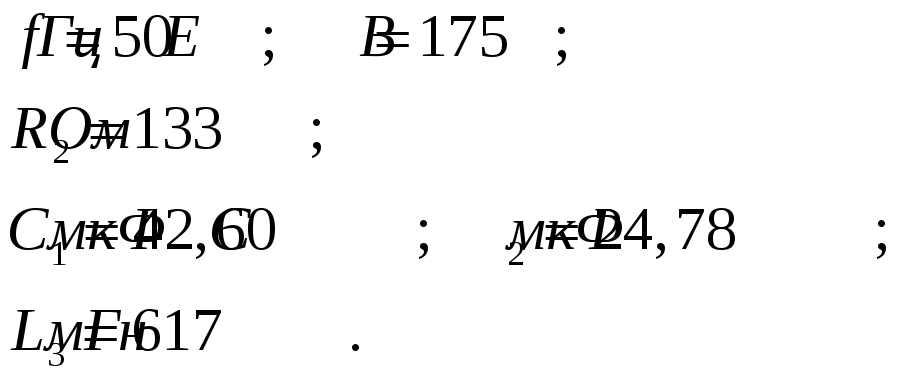
Решение.

.

.

Сопротивления реактивных элементов:

Комплексные сопротивления ветвей:

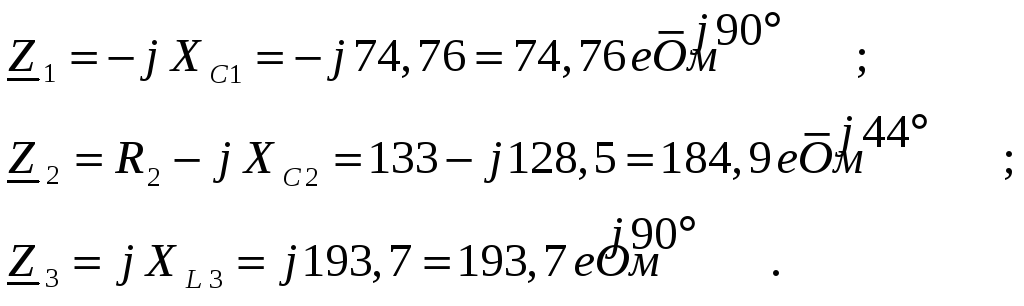
Полное сопротивление цепи относительно зажимов источника ЭДС:

Ток в неразветвленной части цепи:

.

Токи в параллельных ветвях:

Напряжения на участках цепи:

Полная комплексная мощность источника ЭДС

.

Активная, реактивная и полная мощности источника

.

.

Активные и реактивные мощности на участках цепи:

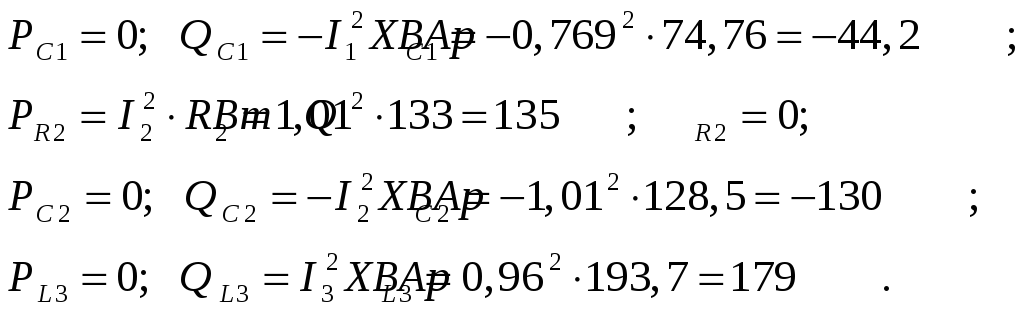
Баланс активной мощности:

.

Баланс реактивной мощности:

.

Баланс полной мощности:

.

Баланс мощности соблюдается.

Векторные диаграммы токов и напряжений:

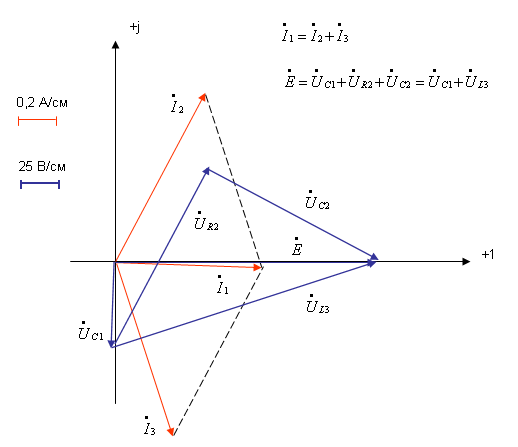
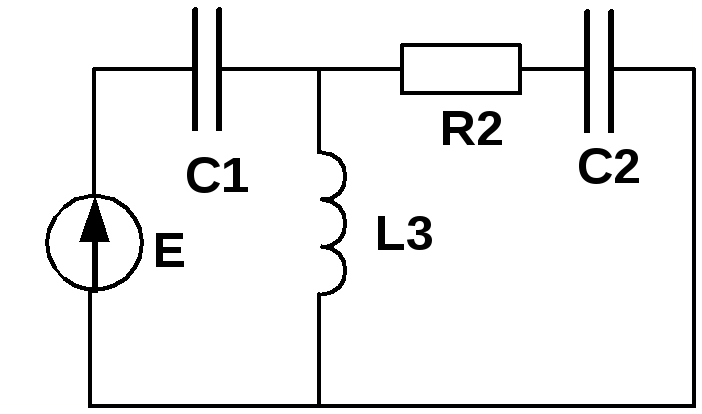
Задача 3

Рассчитать линейную электрическую цепь с несинусоидальной ЭДС, изменяющейся по закону:

Данные для расчета и схема электрической цепи такие же, как в задаче 2. Амплитуда гармоники тройной частоты и постоянная составляющая определяются следующим образом:

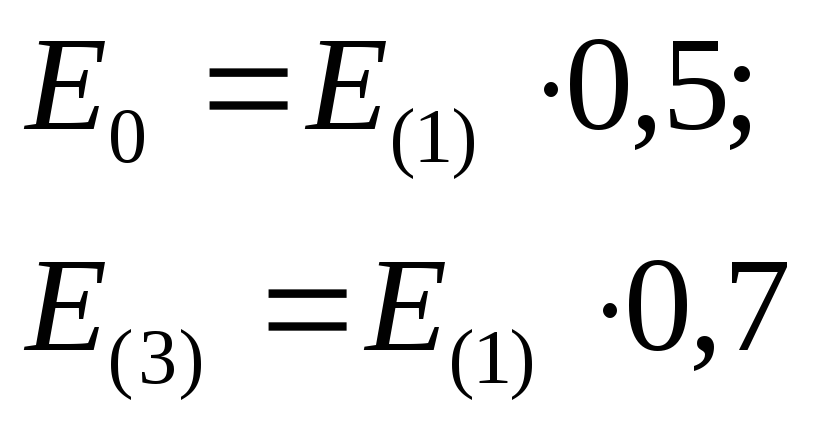
По результатам расчета построить графики изменения токов в ветвях, определить полную, активную, реактивную мощности, мощность искажения цепи.

2.10

Решение.

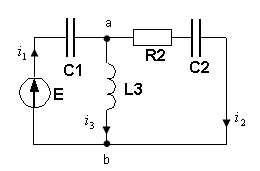
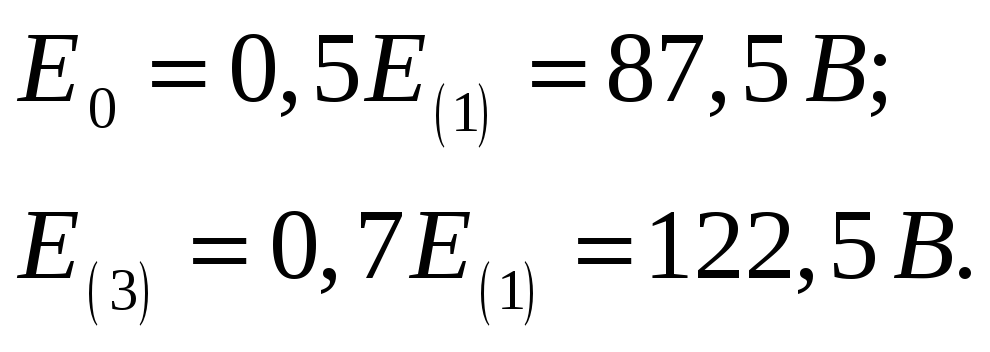
Амплитуды первой и третьей гармоник ЭДС

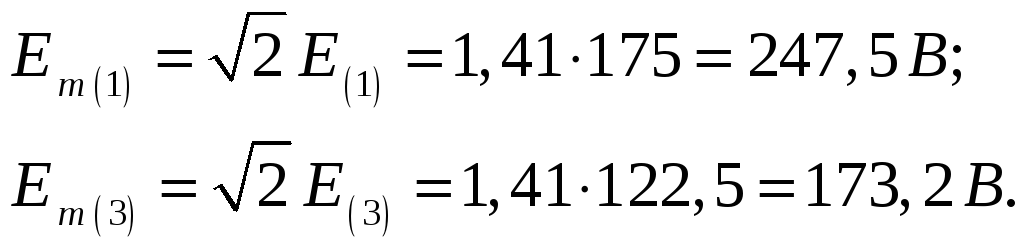
Несинусоидальная ЭДС

.

.

1. Расчет постоянной составляющей.

Постоянная составляющая ЭДС .

Сопротивление емкостей по постоянному току .

Сопротивление индуктивности по постоянному току .

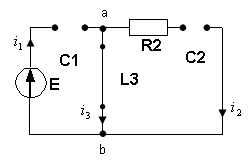
Цепь разомкнута, токи в ветвях равны нулю.

.

2. Расчет 1-й гармоники .

.

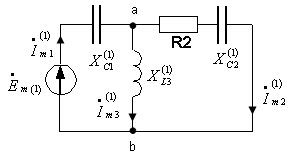
Сопротивления реактивных элементов (вычислено в задаче 2):

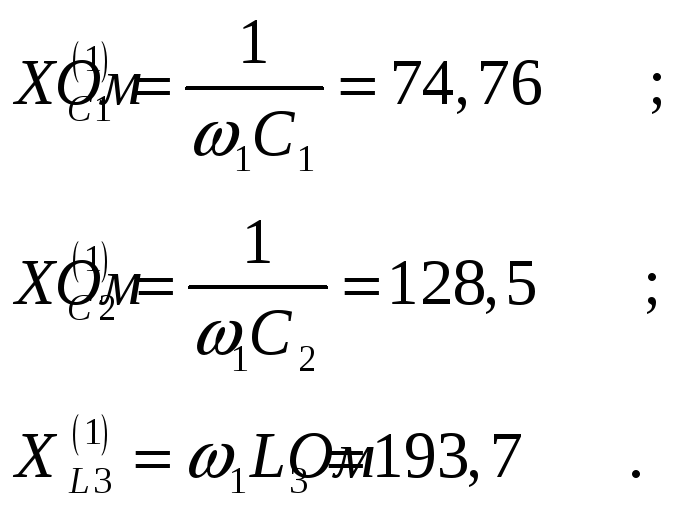
Комплексные сопротивления ветвей (вычислено в задаче 2):

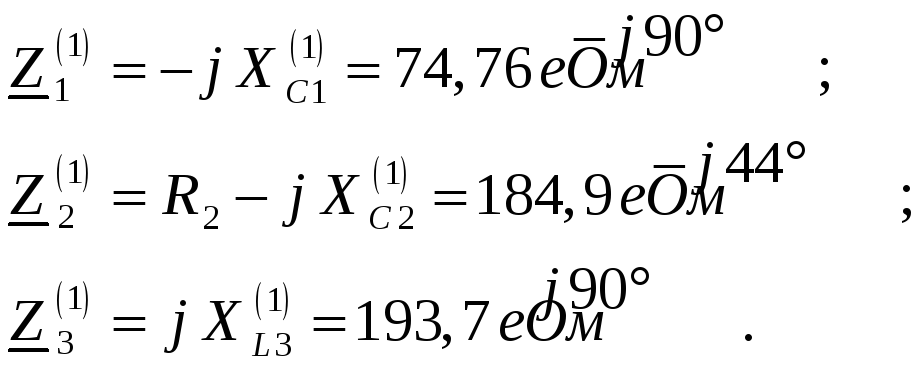
Полное сопротивление цепи относительно зажимов источника ЭДС (вычислено в задаче 2):

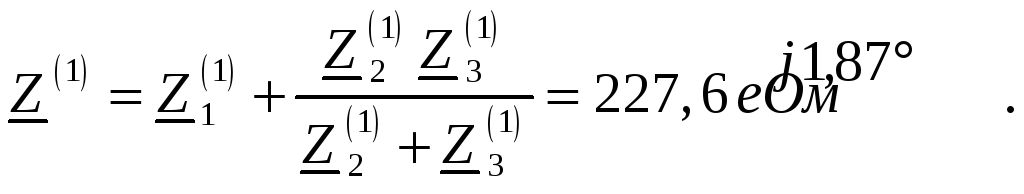
Амплитуда первой гармоники тока в неразветвленной части цепи:

.

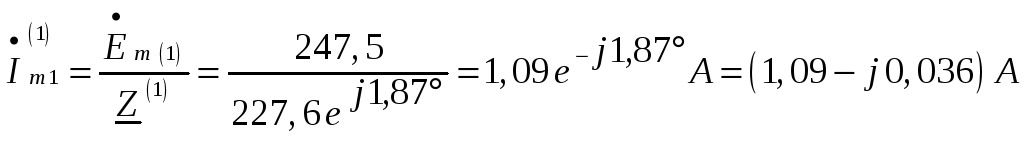Амплитуды первой гармоники токов в параллельных ветвях:

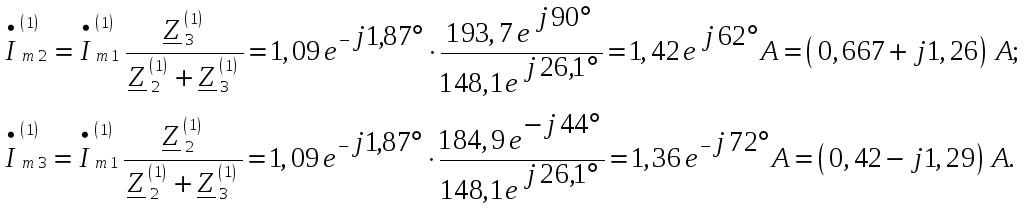
Первые гармоники токов

3. Расчет 3-й гармоники .

.

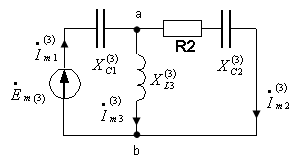
Сопротивления реактивных элементов:

Комплексные сопротивления ветвей:

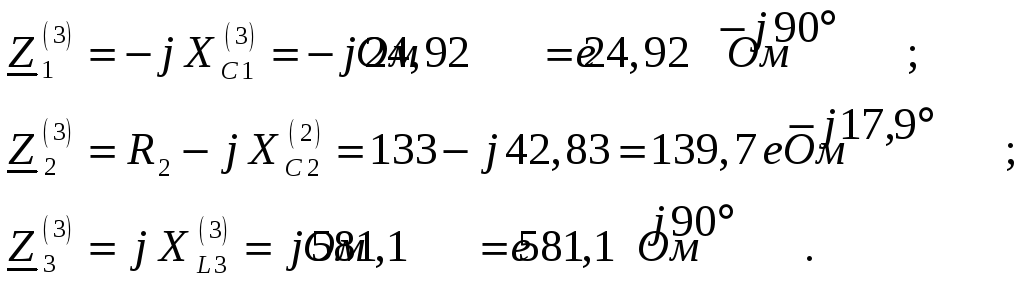
Полное сопротивление цепи относительно зажимов источника ЭДС:

Амплитуда третьей гармоники тока в неразветвленной части цепи:

.

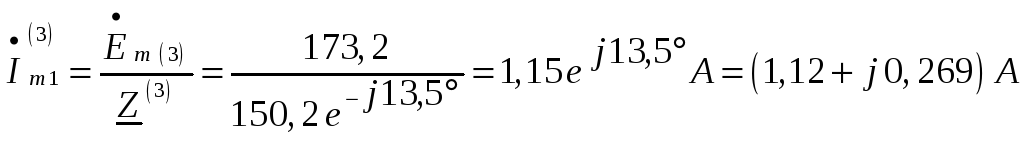Амплитуды третьей гармоники токов в параллельных ветвях:

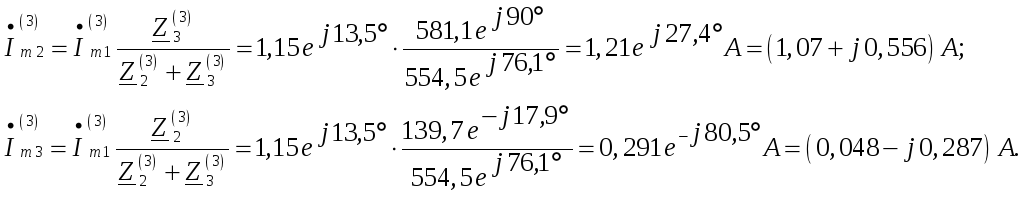
Третьи гармоники токов

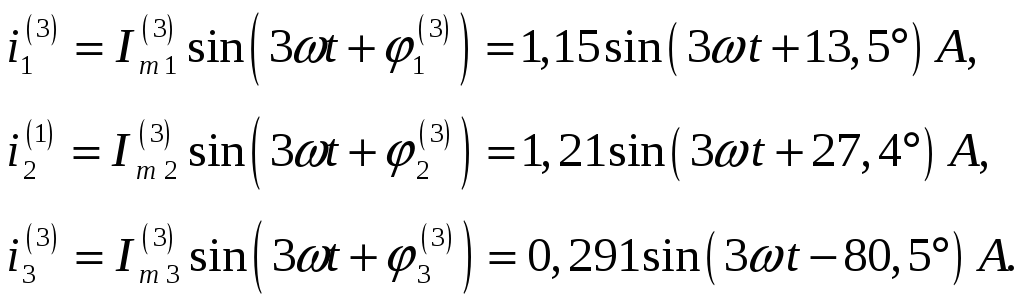
4. Полные токи

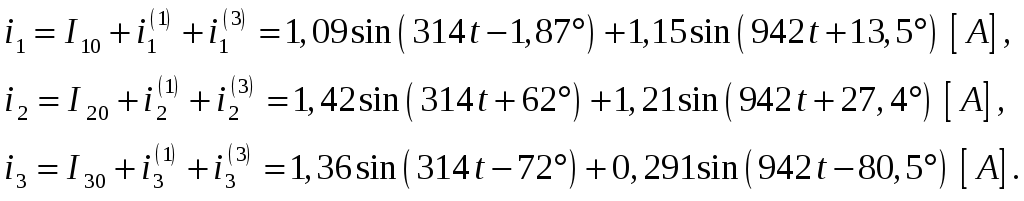
5. Действующее значение ЭДС

.

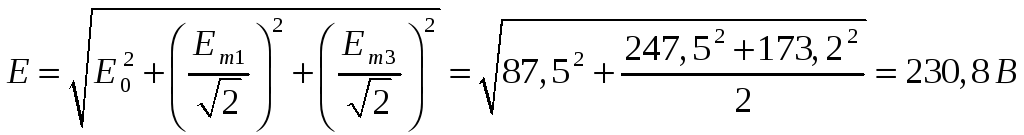Действующее значение входного тока

.

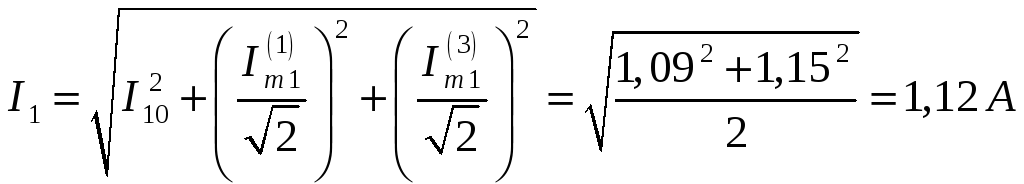Полная мощность цепи

.

Активная мощность цепи

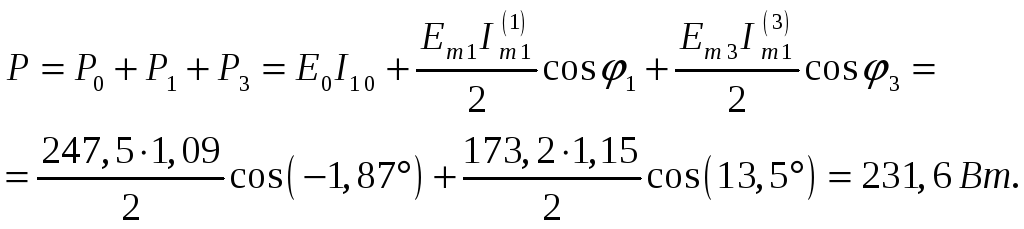
Реактивная мощность цепи

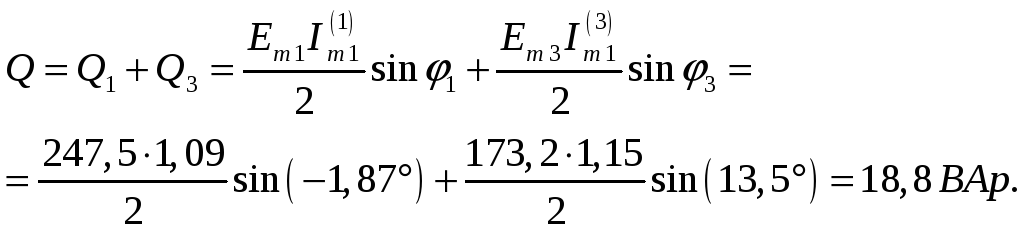
Мощность искажения

.

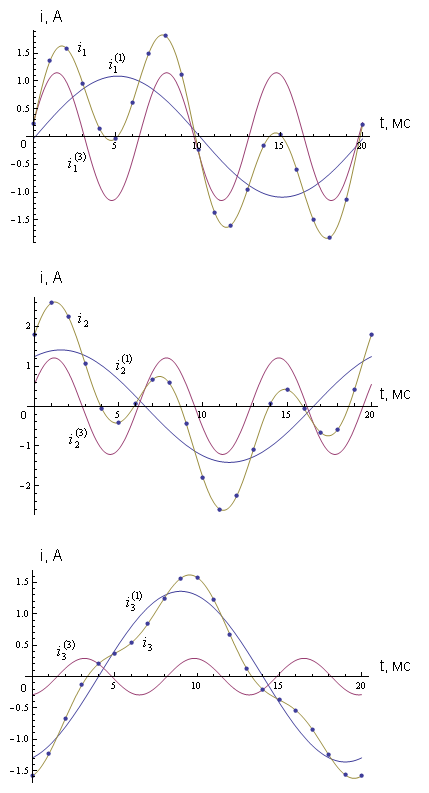
6. Графики изменения токов в ветвях.

Период первой гармоники .

Период третьей гармоники .

t, мс	0	1	2	3	4	5	6	7	8	9	10
i1, A	0,23	1,59	0,15	0,6	1,82	-0,23	-1,59	-0,15	-0,6	-1,82	0,22
i2, A	1,8	2,25	-0,07	0,06	0,58	-1,8	-2,25	0,06	-0,06	-0,58	1,79
i3, A	-1,58	-0,67	0,2	0,52	1,25	1,58	0,67	-0,2	-0,54	-1,25	-1,58

t, мс	11	12	13	14	15	16	17	18	19	20
i1, A	1,59	0,16	0,6	1,82	-0,21	-1,6	-0,16	-0,59	-1,82	0,23
i2, A	2,26	-0,06	0,05	0,58	-1,78	-2,26	0,05	-0,05	-0,59	1,8
i3, A	-0,67	0,2	0,54	1,24	1,58	0,67	-0,2	-0,53	-1,24	-1,58