2.7. Волновая и квантовая оптика

Пример 1. В опыте Юнга отверстия освещались монохроматическим светом с длиной волны  = 600 нм. Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана l = 3 м. Найти положение на экране четырех первых светлых полос.

Решение. В опыте Юнга наблюдается явление интерференции света, которое выражается в его ослаблении или усилении. Так как по условию задачи выполняется одно из условий интерференции: ld, то можно воспользоваться формулой для нахождения координат максимумов интенсивности света

,

где k = 0,1,2,3,...

Все параметры формулы заданы условием задачи. Проведем расчеты при различных значениях k:

(светлая, самая яркая полоса напротив отверстия);

;

3,610^-3 м =

=  3,6 мм;

мм.

Светлые полосы располагаются симметрично отно-сительно центральной полосы (k = 0).

Пример 2. На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки d, чтобы в направлении совпадали максимумы двух линий: нм и нм?

Решение. При прохождении света через дифракционную решетку максимум будет наблюдаться при условии

,

где k - порядок дифракционного максимума.

Знаки "" указывают, что максимумы симметричны относительно нулевого (k = 0, ).

Из условий задачи следует, что

,

или . Отсюда =656,3/410,2=1,6.

Так как числа k₁ и k₂ должны быть обязательно целыми, то полученному отношению удовлетворяют значения k₁ = 5 и k₂ = 8. Тогда

м.

Пример 3. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, равна мкм. Определить энергетическую светимость R_T тела.

Решение. По закону Стефана – Больцмана энергетическая светимость абсолютно черного тела пропорциональна четвертой степени термодинамической температуры и рассчитывается по формуле

, (1)

где  - постоянная Стефана-Больцмана;

T - термодинамическая температура.

Температуру T можно выразить, используя закон смещения Вина:

, (2)

где м/К - постоянная Вина.

Используя формулы (1) и (2), получаем

.

Произведем вычисления:

Вт/м².

Пример 4. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовым излучением с длиной волны нм.

Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта

, (1)

где h - постоянная Планка;

с - скорость света в вакууме;

А - работа выхода электронов, определяемая по таблице (табл. 6 приложения);

m - масса покоя электрона.

Отсюда

. (2)

Подстановка значений констант и значений вели-чин, заданных в условии задачи, в формулу (2) дает

=

= 1,0810⁶ м/с.

2.8. Физика атома и атомного ядра

Пример 1. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность по-тенциалов U. Найти длину волны де Бройля , если: 1) U₁ = 51 В; 2) U₂ = 510 кВ.

Решение. Длина волны де Бройля частицы зависит от ее импульса р и рассчитывается по формуле

, (1)

где h - постоянная Планка.

Импульс частицы можно определить, если известна ее кинетическая энергия . Связь импульса с кинетической энергией различна для нереляти-вистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда они сравнимы между собой).

В нерелятивистском случае

, (2)

где - масса покоя частицы.

В релятивистском случае

, (3)

где - энергия покоя частицы.

В нерелятивистском случае из формулы (1) и соот-ношения (2) следует:

. (4)

В релятивистском случае из формулы (1) и соот-ношения (3) следует:

. (5)

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U₁ = 51 В и U₂ = 510 кВ, с энергией покоя электрона Е_о = m_oc² = 0,51 МэВ и в зависимости от этого решим, какую из только что полученных формул следует применить для вычисления длины волны де Бройля.

Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна E_k = еU.

В первом случае МэВ, что много меньше энергии покоя электрона. Следовательно, для вычисления можно применить формулу (4). Для упрощения расчетов заметим, что Подставив это выражение в формулу (4), перепишем ее в виде

.

Учитывая, что есть комптоновская длина волны , получаем

.

Подставив сюда значение пм, находим

155 пм.

Во втором случае кинетическая энергия МэВ, т.е. равна энергии по-коя электрона. Для вычисления необходимо при-менить формулу (5):

1,27 пм.

Пример 2. Кинетическая энергия электрона в атоме водорода составляет величину порядка =10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.

Решение. Соотношение неопределенностей для координаты и импульса имеет вид

xp  , (1)

где х - неопределенность координаты частицы (в данном случае электрона);

р - неопределенность импульса электрона;

- постоянная Планка (h/2).

Из соотношения неопределенностей следует, что, чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с

неопределенностью

х = l/2.

Соотношение неопределенностей (1) можно записать в этом случае в виде

(l/2)р  ,

откуда

l  p.

Неопределенность импульса не должна превышать значение самого импульса р, т.е. р  р. Импульс р связан с кинетической энергией соотношением . Заменим р значением . (Такая замена не увеличит величину l.) Переходя от неравенства к равенству, получим

= /. (2)

Проверим размерность . Для этого в правую часть формулы (2) вместо символов величин подставим их единицы измерения:

= м.

Найденная единица измерения является единицей измерения длины.

Произведем вычисления:

м.

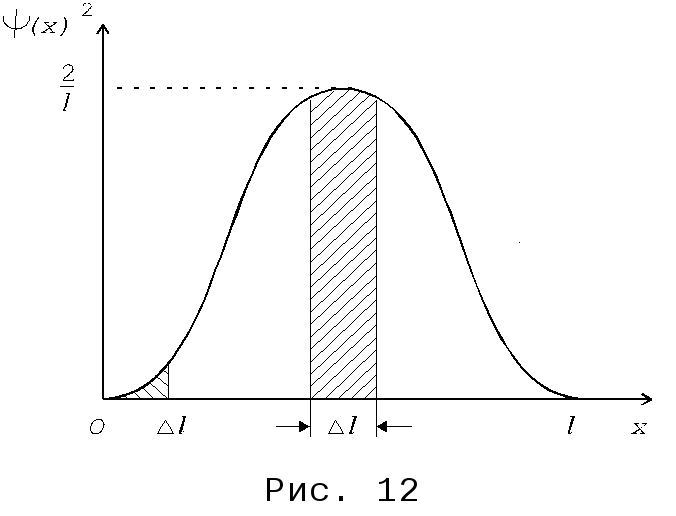
Пример 3. Волновая функция описывает состояние частицы в бесконечно глубокой потенциальной яме шириной l. Вычислить вероятность

нахождения частицы в малом интервале l, состав-ляющем 1% от ширины ямы, в двух случаях:

1) вблизи стенки (0  х  l);

2) в средней части ямы (l/2 - l/2  х  l/2 + l/2).

Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до x + dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние:

.

В первом случае искомую вероятность можно найти путем интегрирования в пределах от 0 до 0,01l (рис. 12):

. (1)

Знак модуля в выражении (1) опущен, так как функция в данном случае не является комплексной. Поскольку x изменяется в интервале 0  x  0,01l, то x/l  1 и, следовательно, справедливо приближенное равенство

. (2)

С учетом формулы (2) выражение (1) принимает вид

.

После интегрирования получаем

.

Во втором случае нет необходимости в интегрировании, так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (l = 0,01l) практически не изменяется. Искомая вероятность определяется выражением

l,

или

.

Пример 4. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

Решение. Энергия фотона определяется по формуле

.

Здесь неизвестной величиной является частота , которая может быть рассчитана по спектральной формуле

,

где R – постоянная Ридберга (R = 1,110⁷ м^-1);

с – скорость света в вакууме (с = 31 м/с);

m – номер орбиты, на которую перешел электрон;

n – номер орбиты, с которой перешел электрон.

Следовательно, энергия фотона выражается форму-лой

E = hRс.

Подставим в данную формулу значения величин:

Дж.

Пример 5. Вычислить дефект массы и энергию связи ядра Li.

Решение. Масса ядра всегда меньше суммы масс свободных протонов и нейтронов. Дефект массы ядра m определяется по формуле

m = Zm_п + (A - Z)m_н - m_я , (1)

где Z - зарядовое число (атомный номер, или число протонов в ядре);

A - массовое число (число нуклонов, состав-ляющих ядро);

m_п, m_н, m_я - массы протона, нейтрона и ядра соответственно.

В формуле (1) неизвестна масса ядра лития, которая определяется из соотношения

m_я = m_а - Zm_e, (2)

где m_а - масса атома;

m_e - масса электрона.

Подставим соотношение (2) в формулу (1):

m = Zm_п + (A - Z)m_н - m_а + Zm_e. (3)

Массы нуклонов, электрона и атома выразим в атомных единицах массы (а.е.м.), приняв во внимание, что 1 а.е.м.= 1,6610^-27 кг. Тогда после подстановки соответствующих значений в формулу (3) получим

m = 31,00728+41,00867-7,01601+30,00065 = 0,04216 а.е.м.

Выразим m в килограммах:

m = 0,042161,6610^-27 = 710^-29 кг.

Энергия связи определяется по формуле

Е_св = mс² = 710^-29(310⁸)² = 6310^-13 Дж.

Пример 6. Имеется радиоактивный препарат Мg массой m = 0,2 мкг. Определить начальную активность препарата А_о и активность препарата А через t = 5 ч. Период полураспада магния = 10 мин.

Решение. Активность изотопа характеризует скорость радиоактивного распада и равна отношению числа ядер dN, распавшихся за интервал времени dt, к этому интервалу:

А = - dN/dt. (1)

Знак "-" показывает, что число радиоактивных ядер N со временем убывает. Для нахождения отношения dN/dt воспользуемся законом радио-активного распада

, (2)

где N - число радиоактивных ядер, содержащихся в изотопе в момент времени t;

N_о - число радиоактивных ядер в момент времени, принятый за начальный (t = 0);

- постоянная радиоактивного распада.

Продифференцируем выражение (2) по времени:

. (3)

Из формул (1) и (3) следует, что активность препарата A в момент времени t равна

. (4)

Если в формулу (4) подставить t = 0, получим на-чальную активность препарата А_о:

А_о=N_о. (5)

Постоянная радиоактивного распада связана с периодом полураспада соотношением

. (6)

Число радиоактивных ядер N_о, содержавшихся в изотопе в момент времени, когда его масса была равна m, определяется соотношением

, (7)

где - молярная масса изотопа;

N_А - число Авогадро.

С учетом выражения (7) формулы (5) и (4) принимают вид

;

. (8)

Произведем вычисления, учитывая, что:

1) = 10 мин = 600 с;

2) ;

3) t = 6 ч = 63,610³ с = 2,1610⁴ с.

Бк;

Бк.