Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Вологодский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodichka_po_Vysshey_Matematike_4_semestr

.pdf

Скачиваний:

Добавлен:

28.05.2015

Размер:

777.55 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Математика : метод. указания и контрол. задания для студентов заоч. формы обучения: (IV семестр): ФЗДО: спец. инженер.-техн./ А. А. Аваев, С. А. Иконникова

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра высшей математики

МАТЕМАТИКА

Методические указания и контрольные задания для студентов заочной формы обучения

(IV семестр)

Факультет заочного и дистанционного обучения

Специальности инженерно-технические

Вологда

2010

Вологодский государственный технический университет. Научно-техническая библиотека

УДК: 517.3

Математика: методические указания и контрольные задания для студентов заочной формы обучения (IV семестр). – Вологда: ВоГТУ, 2010. – 36 с.

В методических указаниях рассматриваются основные типы задач курса математики, изучаемые в IV семестре студентами заочной формы обучения всех инженерно-технических специальностей Вологодского государственного технического университета. Решения всех типов задач разобраны с достаточно подробными комментариями. Контрольные задания содержат варианты задач для самостоятельного решения.

Утверждено редакционно-издательским советом ВоГТУ

Составители: А.А. Аваев, канд. техн. наук, доцент кафедры высшей математики; С.А. Иконникова, ст. препод. кафедры высшей математики

Рецензент О.И. Микрюкова, канд. физ.-мат. наук, доцент кафедры высшей математики

Вологодский государственный технический университет. Научно-техническая библиотека

Введение

Настоящие методические указания служат руководством для студентовзаочников при самостоятельном выполнении контрольных заданий, запланированных в IV учебном семестре. С их помощью в условиях дефицита учебной литературы по математике студент-заочник может самостоятельно разобраться в основных типах задач и без посторонней помощи справиться с выполнением контрольных заданий.

1. Теория поля

1.1. Дана функция z = 6 × x × 3 y × z 2 и точки M1 (1;1;2), M 2 (− 1;2;1). Вычислить:

1) производную от этой функции в точке M1 по направлению вектора

M1M 2 ;

2) (gradu )M1 .

		Решение.
Известно,	что производная от функции u(x, y, z ) в точке M1 по направле-
		находится по формуле
нию вектора M1M 2
	¶u	= u¢x (M1 )× cosa + u¢y (M1 )× cosb + u¢z (M1 )cos g ,

	¶l M1

где cosα,cosβ,cos γ − направляющие косинусы вектора M1M 2 или проек-

ции единичного вектора l 0


		M1M 2

	0 =		=		- 2i		+ j - k				= -	2		+		1				-	1
l																						k
													i						j
				(- 2)2 + 12 + (-1)2									i						j
		M1M 2		(- 2)2 + 12 + (-1)2						6			6					6
на оси координат, т.е.
		cosa = -			2	, cosb =			1	, cos g = -					1		.
		cosa = -				, cosb =		6		, cos g = -							.
				6				6					6

С учетом того, что

Вологодский государственный технический университет. Научно-техническая библиотека

u¢

(x, y, z )

= 6 ×

× 3 y × z 2 =

3 × 3 y × z 2

2 x

u¢ (M

) = u¢ (1;1;2) =

3 × 3 1 × 22

=12 ,

u¢

(x, y, z ) = 6 × x ×

× y − 2 3 × z 2 =

2 × x × z 2

u¢ (M

) = u¢ (1;1;2) =

2 × 1 × 22

= 8 ,

3 12

u¢

(x, y, z )

= 6 × x × 3

y × 2z =12 × x × 3 y × z ,

u¢z (M1 ) = u¢z (1;1;2) =12 × 1 × 3 1 × 2 = 24 ,

получим

¶u			2		1			1		40
	=12 ×	-		+ 8 ×		+ 24 ×	-		= -		.

¶l M1			6		6			6		6

Т.к. градиент функции u(x, y, z ) в точке M1 находится по формуле

(gradu)M1 = u¢x (M1 )× i + u¢y (M1 )× j + u¢z (M1 )× k ,

′

(M1 ),

′

(M1 ), получим

то, используя найденные ранее значения ux

(M1 ), u y

(gradu)M1 =12i

+ 8

= {12;8;24}.

+ 24k

¶u

; (gradu)M1

= {12;8;24}.

Ответ:

= -

¶l M1

1.2. Вычислить поток Π векторного поля

F (x, y, z ) = (x + 2 y - z )i + (y + 2z ) j - 2xk

через часть плоскости p : x + 3y + 2z − 6 = 0 , ограниченную координатными плоскостями.

Решение.

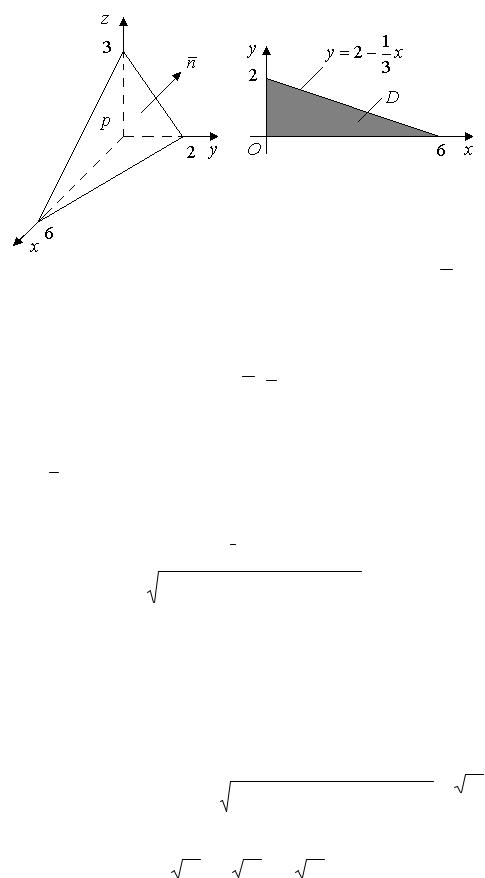
Рассматриваемая часть плоскости p и ее проекция D на плоскость xOy

изображены на рисунке.

Вологодский государственный технический университет. Научно-техническая библиотека

Поток Π векторного поля, заданного векторной функцией F (x, y, z ), че-

рез поверхность S находится с помощью интеграла по площади поверхности

Π = ∫∫(F × n )dS ,

где S − в данном случае часть плоскости p , ограниченной координатными плоскостями, n − единичный нормальный вектор поверхности S .

Если поверхность S описывается уравнением z = ϕ(x, y), то

- j¢x (x, y)× i

- j¢y (x, y)×

+ k

n =

(j¢x (x, y))2 + (j¢y (x, y))2 + 1

при этом

составляет с осью Oz острый угол.

Т.к. в рассматриваемом случае

z = j(x, y) =

6 − x − 3y

то

j¢x

(x, y ) = -

, j¢y (x, y) = -

, (j¢x (x, y))2 + (j¢y

(x, y ))2 + 1 =

При этом

Вологодский государственный технический университет. Научно-техническая библиотека

F × n = 1 [(x + 2 y - z )×1 + (y + 2z )× 3 + (- 2x)× 2]= − 3x + 5 y + 5z = f (x, y, z ). 14 14

Т.к. известно,													что интеграл по площади поверхности S																																			может быть вы-
числен с помощью двойного интеграла по области D по формуле
∫∫ f (x, y, z )dS = ∫∫ f (x, y,j(x, y))×																											(j¢x (x, y))2 + (j¢y (x, y))2 +1 × dxdy ,
S																D
то
Π = ∫∫(												×			)dS = ∫∫						1		- 3x + 5 y + 5 ×											6 - x - 3y												×		14	×dxdy =
									F
														n
														n							14																											2
		S																	D		14																			2								2
		S																	D
																																	2−			1	x
																														6			2−				x
					1																								1	6					3
	= -				1			∫∫(11x + 5 y - 30)dxdy = -																					1	∫dx					∫(11x + 5 y - 30)dy =
	= -							∫∫(11x + 5 y - 30)dxdy = -																						∫dx					∫(11x + 5 y - 30)dy =
			4							D																		4		0					0
										D																				0					0
																		6																	2 −			1		x		dx =
																																						1

																= - 1 ∫ 11xy + 5 y 2 - 30 y																					3
																																					3

																		4								2											0
																		0
											6
						1					6										1			5						1		2													1
	= -										∫		11x ×					2 -				x	+			× 2	-				x				-		30 × 2 -										x dx			=
	= -					4					∫		11x ×					2 -				x	+	2		× 2	-				x				-		30 × 2 -								3		x dx			=
						4					0										3			2						3															3
											0
	1	6									61					2		86										1				61					3					43		2							6
	1	6									61					2		86										1				61					3					43		2							6
= -		∫ -													x		+			x - 50 dx = -										-					x					+			x			-		50x				= 7 .
= -	4	∫ -									18				x		+	3		x - 50 dx = -								4		-		54			x					+		2	x			-		50x				= 7 .
	4	0									18							3										4				54										2									0
		0
Ответ: Π = 7 .
1.3. Вычислить поток Π векторного поля, заданного функцией
							(x, y, z ) = (x2 z - y)× i																		+ (2 y + z 2 + 1)×																+ (xy - z )× k								,
				F			(x, y, z ) = (x2 z - y)× i																		+ (2 y + z 2 + 1)×														j		+ (xy - z )× k								,

через замкнутую поверхность

S : z =1 - x2 - y 2 ; x + y =1; x = 0; y = 0; z = 0 .

Решение.

Рассматриваемая поверхность и ее проекция D на плоскость xOy изо-

бражены на рисунке.

Вологодский государственный технический университет. Научно-техническая библиотека

Известно, что поток Π векторного поля, заданного векторной функцией

F (x, y, z ) через замкнутую поверхность S в направлении внешней нормали

(т.е. изнутри наружу), может быть вычислен по формуле ОстроградскогоГаусса

Π = ∫∫∫divF × dv ,

где V − часть пространства, ограниченная замкнутой поверхностью S ; divF − дивергенция векторного поля.

Если F (x, y, z ) = P(x, y, z )× i + Q(x, y, z )× j + R(x, y, z )× k , то

	= ∂P +	∂Q +		∂R .
divF	= ∂P +	∂Q +		∂R .
	¶x	¶y		¶z
В рассматриваемом случае:
P(x, y, z ) = x2 z - y;			∂P = 2xz;
			¶x
Q(x, y, z ) = 2 y + z 2 + 1;				∂Q = 2;
				¶y
R(x, y, z ) = xy - z;			∂R = -1;
			¶z

divF = 2xz + 1.

Таким образом

Π = ∫∫∫(2xz +1)dv =

Вологодский государственный технический университет. Научно-техническая библиотека

	1	1− x 1− x 2 − y 2
	= ∫dx ∫ dy		∫(2xz + 1)dz =
	0	0	0
1	1− x
= ∫dx ∫(1 + x - x2 + x5 - y 2 - 2xy2 + 2x3 y 2 + xy 4 )dy =
0	0

Ответ: Π = 2 . 5

1.4. С помощью формулы Стокса вычислить циркуляцию Ц векторного

поля, заданного функцией

F (x, y, z ) = (x2 + y 2 + z 2 )× i + (x2 - y 2 + 3z 2 )× j + (- x2 + 2 y 2 - z 2 )× k ,

по контуру ABCA треугольника с вершинами A(1;0;0), B(0;1;0),C(0;0;1).

Решение.

Рассматриваемый треугольник и его проекция D на плоскость xOy

изображены на рисунке.

Циркуляция Ц векторного поля, заданного векторной функцией

F (x, y, z ) = P(x, y, z )× i + Q(x, y, z )× j + R(x, y, z )× k ,

по замкнутому контуру L может быть рассчитана по формуле Стокса

Ц = ∫ P(x, y, z )dx + Q(x, y, z )dy + R(x, y, z )dz = ∫∫(rotF × n )dS ,

L S

где rotF - ротор (вихрь) векторного поля; n − единичный нормальный вектор поверхности S , натянутый на контур L .

Вологодский государственный технический университет. Научно-техническая библиотека

Известно, что

rotF =

¶x

¶y

¶z

P(x, y, z )

Q(x, y, z )

R(x, y, z )

¶R

¶Q

¶R

¶P

¶Q

¶P

× j

× k .

× i -

¶y

¶x

¶z

¶x

¶z

¶y

При использовании формулы Стокса предполагается, что если смотреть с конца вектора n вдоль него, то обход контура L будет виден совершающимся против движения часовой стрелки.

Т.к. в рассматриваемом случае

P(x, y, z ) = x2 + y 2 + z 2 , Q(x, y, z ) = x2 - y 2 + 3z 2 , R(x, y, z ) = -x2 + 2 y 2 - z 2 ,

то

rotF =

¶x

¶y

¶z

x2 + y 2 + z 2

x2 - y 2 + 3z 2 - x2 + 2 y 2 - z 2

= (4 y - 6z )× i

+ (2x + 2z )×

+ (2x - 2 y )× k

На контур L в данном случае натянут

треугольник ABC , при этом

уравнение плоскости S , в которой он расположен, можно описать как урав-

нение плоскости «в отрезках»

=1 z =1 - x - y S :z = j(x, y ) =1 - x - y .

Т.к.

- j¢x (x, y )× i

- j¢y (x, y )×

+ k

n =

, j¢x (x, y ) = -1, j¢y (x, y) = -1,

(j¢x

(x, y))2 + (j¢y

(x, y ))2 + 1

то

× k

× i

Вологодский государственный технический университет. Научно-техническая библиотека

При этом

Ц = ∫∫(rot		×		)dS =	2	× ∫∫(2x + y - 2z )dS .
	F
			n
					3
S						S

Т.к. при переходе от интеграла по площади поверхности S к двойному интегралу по области D − проекции S на координатную плоскость xOy

используется известная формула

∫∫ f (x, y, z )dS = ∫∫ f (x, y,j(x, y))×			(j¢x (x, y))2 + (j¢y (x, y))2 + 1 × dxdy ,
S		D
то в данном случае
Ц =	2	× ∫∫(2x + y - 2(1 - x - y))×	3 × dxdy = 2 × ∫∫(4x + 3y - 2)dxdy =
	3
		D	D

11− x

=2 × ∫dx ∫ (4x + 3y - 2)dy = 1 .3

0 0

Ответ: Ц = 1 . 3

2. Элементы теории функций комплексной переменной и операционного исчисления

2.1. Определить действительную u(x, y ) и мнимую v(x, y ) части функции w = 4z - 2iz 2 + 3z3 .

Решение

Т.к. z = x + iy ( x = Re z, y = Im z − действительная и мнимая части комп-

лексного числа z , соответственно; i = -1 - мнимая единица), то w = 4 × (x + iy) - 2i × (x + iy)2 + 3 × (x + iy)3 =

= 4x + 4iy - 2i × (x2 + 2ixy - y 2 )+ 3 × (x3 + 3ix2 y - 3xy 2 - iy3 )= = 4x + 4xy + 3x3 - 9xy 2 + i × (4 y - 2x2 + 2 y 2 + 9x2 y - 3y3 ).

При этом с учетом того, что w = u(x, y ) + iv(x, y ), получим u(x, y ) = 4x + 4xy + 3x3 - 9xy 2 ,

Вологодский государственный технический университет. Научно-техническая библиотека

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.08.2019206.34 Кб1METODIchka_po_kulturologii2009_1 (1).doc
#
14.11.20196.2 Mб10metodichka_po_labam.doc
#
28.05.2015256 Кб26Metodichka_po_Metrologii.doc
#
23.09.2019310.78 Кб5Metodichka_po_mirovoy_k_FEPO.doc
#
28.05.2015897.02 Кб18Metodichka_po_TOE.doc
#
28.05.2015777.55 Кб3Metodichka_po_Vysshey_Matematike_4_semestr.pdf
#
24.09.2019264.19 Кб1Metodichka_Prav_obesp_sots-kult_servis_i_tur.doc
#
07.09.2019349.7 Кб5metodichka_russky_z_o_2008.doc
#
28.05.2015632.58 Кб6metod_recomendazii[1].pdf
#
08.11.2018329.73 Кб3metod_ukazania.doc
#
25.03.201662.98 Кб11metod_ukazania_po_kurs_proekt-yu.doc