3. Переход к задаче с однородными граничными условиями

W(x,t)=V(x,t) + U(x,t) (9)

Здесь

U(x,t) = ₁(t) + x/l(₂(t) - ₁(l)) =Ae^t(1-x/l)Sin(t) (10)

удовлетворяет неоднородным граничным условиям. V(x,t) – новая неизвестная функция.

Подставляя (9), (10) в (6)-(8), получим неоднородное уравнение V_{tt +}(²-²)V - a²V_xx = f(x,t), (11)

где

f(x,t) = Ae^t(1-x/l)(²-²).

Начальные условия

V(x,0) =0

V_t(x,0) = -A(1-x/l) . (12)

Однородные граничные условия

V(0,t)=0

V(l,t)=0 (13)

Здесь имеет место перенос неоднородности из граничных условий в уравнение.

4. Решение однородной граничной задачи. Решение уравнения (11) представим в виде:

V(x,t)=V⁰(x,t)+V^*(x,t) (14)

V⁰- удовлетворяет однородному уравнению и неоднородным начальным условиям; V^*- удовлетворяет неоднородному уравнению и однородным начальным условиям. a² V⁰_xx – V⁰_tt – (² - ²) V⁰ = 0. (15)

Начальные условия

V⁰(x,0)=0

V⁰_t(x,0)=-A(1-x/l). (16)

Граничные условия

V⁰(0,t)=0

V⁰(l,t)=0 (17)

Решение уравнения (15) ищем методом Фурье, представляя его в виде

V⁰(x,t) = X(x) T⁰(t) (18)

Подставим(18) в (15) и разделим на XT, получим

(19)

или

(20)

Тогда

(21)

Подставляем (18) в граничные условия (16), получим

(22)

Соотношения (21) и (22 ) представляют собой задачу Штурма-Лиувилля.

Общее решение уравнения(21) имеет вид

(23)

Подставляя (23) в (22), получим

(24)

Для существования ненулевого решения необходимо, чтобы выполнялось

Условие С₁0.

Тогда

sin(l)=0

_nl=n, где n=1,2,3…

Собственные числа задачи равны

Собственные функции при С₁=1 будут иметь вид

(25)

Из уравнения (20) получим

Обозначим

Тогда (26)

Решая дифференциальное уравнение (26) получим

(27)

Решения уравнения (16) представим как сумму частных решений

(28 )

Подставляя (27) в начальное условие (12), получим

(29)

Разложим в ряд Фурье правую часть второго равенства

,

где

Тогда начальные условия (29) будут иметь вид

(30)

Подставляя решение (28) в условия (30), определим A_n и B_n

,.

Тогда

(31)

Подставляя (31) в (27) будем иметь (32)

5. Решение неоднородного учп с однородными начальными и граничными условиями

Представим решение неоднородного уравнения в виде ряда по собственным функциям

(33)

При этом функция удовлетворяет уравнению

(34)

и начальным условиям

Разложим в ряд Фурье правую часть уравнения (34) и подставив в него выражение (32), приравняем коэффициенты при одинаковых . Получим неоднородное обыкновенное дифференциальное уравнение

. (35)

и однородные начальные условия

(36)

Общее решение уравнения (34) представим в виде

T_n(t)=T_n^*(t)+T_n^**(t) , (37)

где T_n^*(t) – общее решение уравнения (35),

T_n^**(t) – частное решение уравнения (35).

Учитывая решение(27) уравнения (26), получим

(38)

Частное решение ищем по виду правой части уравнения (34)

(39)

Подставляя (38) в (34) и прирaвнивая коэффициенты при и, получим

Отсюда находим

, ,

где

(40)

Подставляя (36), (37), (38) в граничные условия (35) определим постоянные A_n^* и B_n^*

(41)

Подставляя (37), (38) и (40) в (36) получим

(42)

Подставляя (42) в(32), а затем в (14) получим

(43)

6. Сборка решения и построение графиков.

Подставляя (43) и (10) в (9), затем в (5),получим окончательное решение

(44)

Определяем производные

(45)

(46)

Для построения графиков зададим параметры задачи

Полученные графики представлены на рис. (2)-(5). На графиках можно проследить распространение и отражение разрывных фронтов от закрепленного края струны. Число членов рядов устанавливалось путем численного эксперимента принималось для функции равным 100, а для производных – 200.

P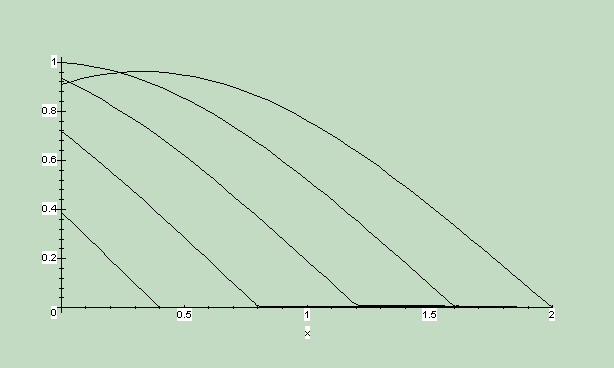ис.2. График функции u(x,t) для t[0,2].

Рис. 3. График функции u(x,t) для t[2,4].

Рис. 4. График производной u_t(x,t) t[0,2]

Рис. 5. График производной u_t(x,t) t[2,4]

Рис. 6. График производной u_x(x,t) t[0,2]

Рис. 7. График производной u_x(x,t) t[2,4]

Пример 2

u

Q₀ x

Рис. 8.