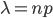9. Определение вероятности. (Достоверное, невозможное, случайное событие.)

Вероя́тность — степень возможности наступления некоторого события.

Достоверное= событие которое точно произойдет его вероятность Р=1

Невозможное- событие которое точно не произойдет его вероятность

   Случайными событиями называются такие события, которые могут произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данных событий.

10. Элементы комбинаторики: число перестановок, размещений, сочетаний.

Вариант упорядочивания данного множества называется перестановкой(Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА)

Если из множества n элементов выбирают m в определенном порядке, это называется размещением(Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ)

Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием(Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ)

11. Совместные и несовместные события; зависимые и независимые события. Полная группа событий. Условная вероятность.

Совместные и несовместные события события которые одновременно произойти могут/не могут

зависимые и независимые события- когда наступление события А зависит/не зависит от наступления события Б

Полная группа событий- множество всех попарно несовмесных (взаимноисключаемых) исходов экспиримета

Условная вероятность- вероятность одного события при условии, что другое событие уже произошло.

12. Сумма вероятностей. Произведение вероятностей.

Сумма вероятностей 2х событий А и Б называется событие при котором происходит либо событие А либо событие Б

Произведение вероятностей- 2х событий А и Б называется событие при котором происходит и событие А и событие Б

13. Формула Бернулли. Область её применения.

формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. , где. Используется при повторных независимых испытаниях

14. Теоремы Лапласа (локальная и интегральная). Формула Пуассона. Области их применения.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n) Для определения значений φ(x) можно воспользоваться специальной таблицей. Когда достаточно многоn

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равнаP(k₁;k₂)=Φ(x'') - Φ(x')Здесь

-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний . При больших значенияхпользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона.,где