дискретка / Лекция 16

Лекция 16.

п.16. Линейное программирование.

16.2. Формы записи ЗЛП.

Модель задачи линейного программирования может быть записана в одной из приведенных ниже форм.

1. Общая, или произвольная, форма записи (ОЗЛП):

,

при ограничениях:

,

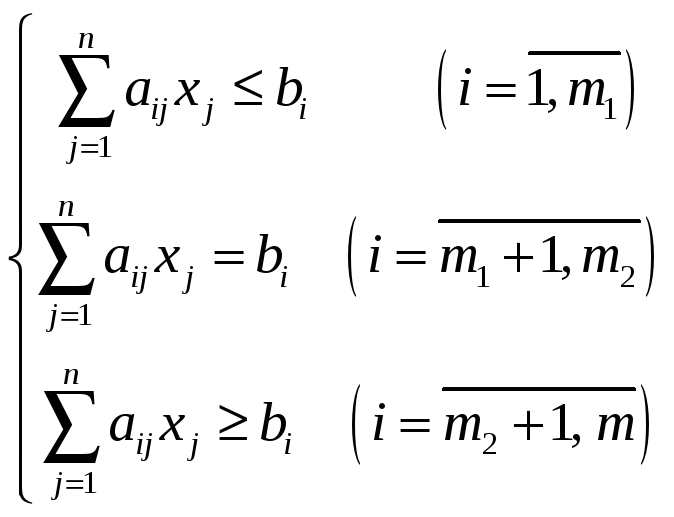- произвольная .

2. Симметричная, или стандартная, форма записи (СФЗЛП):

, ,

, ,

3. Каноническая, или основная, форма записи (КФЗЛП)

,

,

.

Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме, т.е. если имеется способ нахождения оптимального решения задачи в одной из указанных форм, то тем самым может быть определен оптимальный план задачи в любой другой форме (говорят о стратегической эквивалентности задачи в любой из форм).

Так при необходимости задачу минимизации можно заменить задачей максими-зации, и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если – точка минимума функции , то для функции она являя-ется точкой максимума, так как графики функций и симметричны относи-тельно оси абсцисс. Итак,

.

То же самое имеет место и в случае функции n переменных:

.

Неравенство типа путем умножения левых и правых частей на 1 можно превратить в неравенство типа , и наоборот. Ограничения-неравенства

преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных :

.

В случае необходимости ограничение-равенство

можно записать в виде системы неравенств

.

Если в ЗЛП какая-то переменная не подчиняется условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных и :

.

Вводимые дополнительные переменные имеют определенный экономический смысл, прямо связанный с содержанием задачи. Так, в задачах об использовании ресурсов они показывают величину неиспользованного ресурса, в задачах о смесях – потребление соответствующего компонента сверх нормы.

Рассмотрим на примерах, как можно делать переход от одной формы записи к другой.

Пример 6.3. Привести к канонической форме записи ЗЛП:

;

.

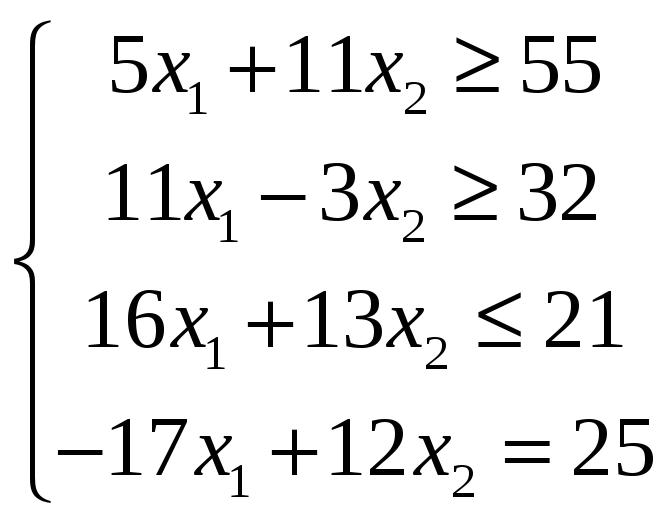Решение. Заменяем функцию Z на . Из левых частей ограничения типа  вычитаем неотрицательные переменные , а к левой части ограничения типа  прибавляем неотрицательную переменную . Переменную , которая может быть произвольного знака, заменяем разностью двух неотрицательных переменных:

.

В результате получаем модель задачи в каноническом виде:

;

. 

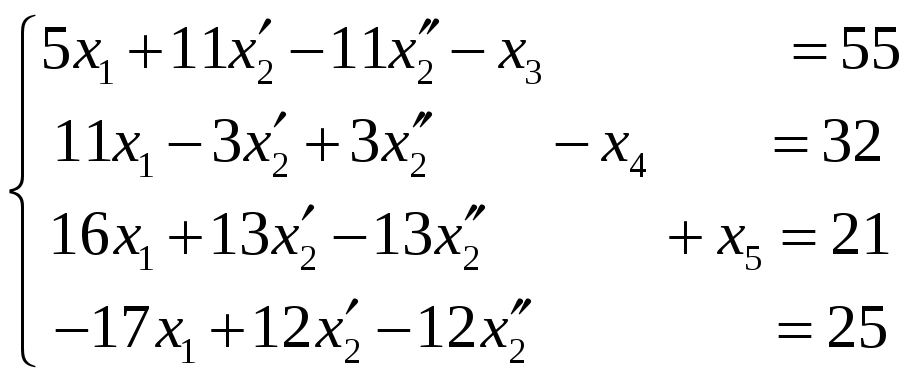Пример 6.4. Привести к симметрической форме записи задачу, заданную в виде:

;

.

Решение. Так как целевая функция по условию максимизируется, то все ограни-чения в канонической форме записи должны быть типа . Поскольку в систему ограничений входит три неравенства, то исключим из системы любые три переменные. В данном случае удобно исключить из первого ограничения , из второго  и из третьего  .Учитывая неотрицательность переменных, получаем:

.

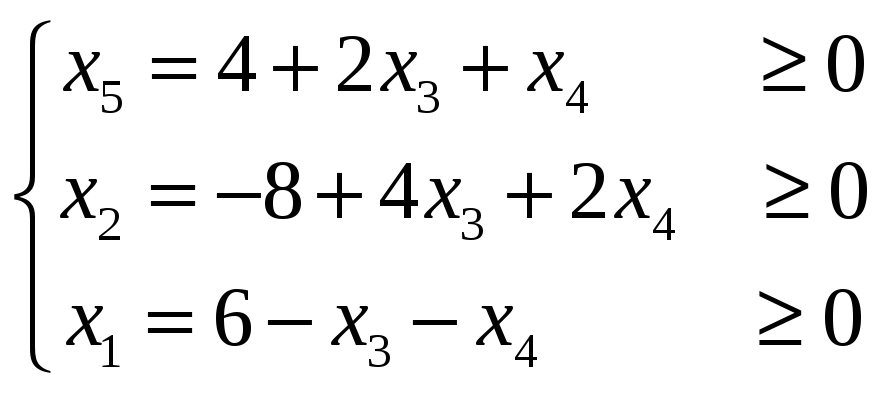Подставив в целевую функцию, получаем:

.

Опустив , придем к эквивалентным неравенствам. В результате получаем следующую ЗЛП в симметрической форме:

.


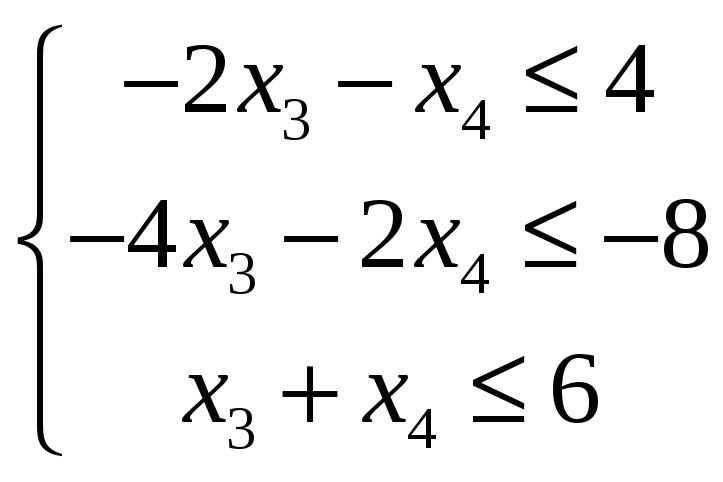