Лекция 5. П.5. Булевы функции.

5.2. Существенная и фиктивная переменная.

Введенное выше понятие функции несовершенно, поскольку оно не позволяет рассматривать функцию от меньшего числа аргументов как функции от большего числа первоначальных аргументов. Для устранения этого недостатка введем следующее определение.

Определение 5.2.ФункцияизP₂зависит существенноот аргументаx_i, если существуют такие значенияa₁, …,a_i-1,a_i+1,…,a_n переменныхx₁, …,x_i-1,x_i+1, …,x_n, что

.

В этом случае переменная x_iназываетсясущественной, в противном случае называетсянесущественной(фиктивной) переменной.

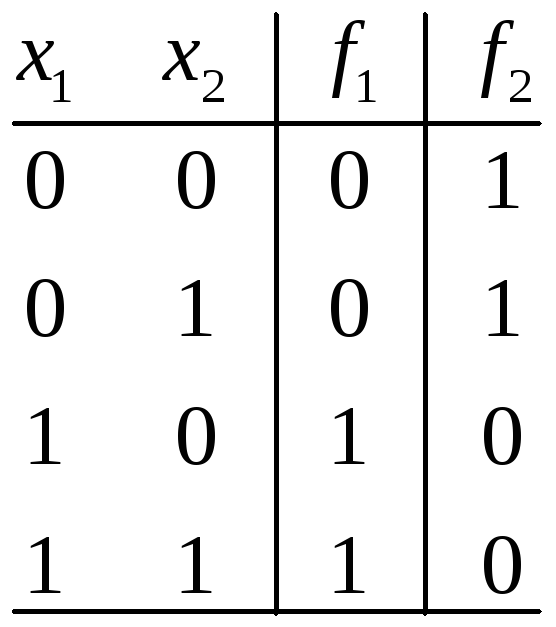
Пример ..Пусть булевы функцииf₁(x₁,x₂) иf₂(x₁,x₂) заданы таблицей истинности:

.

Для этих функций переменная x₁– существенная, а переменнаяx₂– фиктивная.



Пусть для функции переменнаяx_iявляется фиктивной. Возьмем таблицу для функциии по ней построим новую таблицу путем вычеркивания всех строк вида и вычеркивания столбца для аргументаx_i. Полученная таблица будет определять некоторую функцию . Будем говорить, что функция получена изпутем удаления фиктивной переменнойx_i, а также, что функцияполучается из путем введения фиктивной переменнойx_i.

Определение 5.3.Функцииf₁иf₂называютсяравными, если функциюf₂можно получить изf₁путем введения и (или) удаления фиктивных переменных.

В дальнейшем всюду функции рассматриваются с точностью до фиктивных переменных, т.е. мы считаем, что если задана функция f₁, то задана и любая равная ей функцияf₂. Это накладывает некоторые естественные ограничения на классы функций, которые будут здесь рассматриваться. В частности, класс функций, обладающих определенными свойствами, будет рассматриваться только в том случае, если эти свойства инвариантны относительно операций введения и удаления фиктивных переменных.

Существует два типа функций, которые не имеют существенных переменных: функции первого типа тождественно равны 0, а второго – 1. Ввиду этого целесообразно включать в наши рассмотрения константы 0 и 1, рассматривая их как булевы функции от пустого множества переменных.

П.6. Реализация функций формулами.

6.1. Формулы. Реализация функций формулами.

Как известно, в математическом анализе из «элементарных» функций можно составить формулы. Так и из «элементарных» булевых функций можно строить формулы.

Пусть X– некоторый фиксированныйалфавит переменных,=- множествофункциональных символов (базис)и- множество булевых функций, соответствующих функциональным символам, т.е. являющиеся подмножеством множества функцийP₂.

Определение 6.1.Формулой над называется всякое (и только такое) выражение вида:

1) x– любая переменная из множестваX;

2) , гдеA, B– это формулы над.

В дальнейшем будем обозначать формулы прописными буквами латинского алфавита. В тех случаях, когда нужно обратить внимание на множество тех переменных, которые участвуют в построении формулы, пишут . ПустьA– произвольная формула над, тогда формулы, которые использовались для ее построения, будем называтьподформуламиформулыA.

Пример ..Пусть- множество «элементарных» функций.

1) ;

2) ;

3) .

Выражения являются формулами над, а выражениеформулой не является.



Для формул над множеством функциональных символов (логических связок) принимаются некоторые соглашения:

1) внешние скобки у формул опускаются;

2) формула (AB) записывается в виде (AB) или (AB);

3) считается, что связка сильнее любой двуместной связки из множества;

4) связка считается сильнее, чем любая другая двуместная связка из множества.

Сопоставим теперь каждой формуле Gнекоторую функциюf_G. Понятие булевой функцииf_G, реализуемой формулойG, вводится рекурсивно следующим образом:

1) Формуле G=x, гдеxX, сопоставляется функция;

2) если Gравна одной из формул, гдеA,B– это формулы над, тоf_Gравно соответствующей элементарной булевой функции. Если, то значение ее на произвольном наборе, совпадает со значением на этом наборе для соответствующей ей элементарной булевой функции.

Таким образом, зная таблицы истинности элементарных функций (функций базиса), можно вычислить и таблицу истинности функцииf_G, которую реализует формулаG.

Пример ..Пустьf (x₁,x₂) – функция, которой соответствует формула.

Эта формула состоит из трех подформул: ,,. В таблице истинности приводятся соответствующие им функции.

.

Последний столбец определяет функцию f (x₁,x₂). Очевидно, чтоf (x₁,x₂)=x₁x₂.

