6. Длина когерентности, глубина проникновения, сверхпроводники I и II рода.

Пусть на чистую плоскую поверхность сверхпроводника нанесена пленка нормального металла. В глубине сверхпроводника || = 1, а на поверхности несколько мень­ше. Изменение  может происходить только вдоль оси x (вглубь сверхпроводника), то есть  = (x). Для односвязанного сверхпроводника можно считать  вещественной функ­цией, тогда первое уравнение Гинзбурга – Ландау (4.10) принимает простой вид:

.

Пусть (x) = 1 – (x), (x) << 1 (слой нормального металла тонкий). С точностью до линейных по  членов получаем:

,

так как (x  ) = 1. Тогда решение имеет вид:

.

Таким образом,  – это тот характерный масштаб, на кото­ром происходит изменение параметра порядка , он называется длина когерентности. Величина  в соотношении (4.9) – это уже известная глубина проникновения. Из соотношения (4.4) следует, что при Т_С – Т << T_C можно принять  ~ (Т_С – Т)^–1/2,  ~ (Т_С – Т)^–1/2.

Вводится так же очень важная величина – параметр Гинзбурга – Лан­дау :

 = /. (4.17)

Подставляя в выражение (4.17) формулы (4.8) для , (4.9) для  и (4.3) для Н_СМ, получим:

, (4.18)

или

. (4.19)

Энергия границы раздела между n и s фазами

Рассмотрим плоскую SN-границу сверхпроводника первого рода, на­ходящегося в промежуточном состоянии, граница перпенди­кулярна оси x, магнитное поле параллельно оси z. Можно выбрать калибровку, при ко­торой (x) – вещественная функция; A_y(x)  0. Преобразуем уравнения Гинзбурга – Ландау (4.10) и (4.13) к виду:

.

Первый интеграл этих уравнений

,

где константа С находится из граничных условий. Поскольку при х  , то есть в глубине сверхпроводника,   1, d/dx  0, A  0, то С = 1/2. Используя соотношение (4.19), окончательно получаем:

(4.20)

В нормальном металле при x > 0 в промежуточном состоянии магнитное поле всегда равно Н_СМ, то есть внешним полем для сверхпроводящей области будет Н_СМ, поэтому плотность потенциала Гиббса (4.5) в сверхпроводящей области имеет вид:

G_S = F_S – HH_CM/(4). (4.21)

Вдали от границы Н = 0, поэтому G_S0 = F_S0. В нормальном металле (x > 0) плотность свободной энергии составит F = F_N + H_CM²/(8). Тогда плотность потенциала Гиббса в нормальном металле, где Н = Н_СМ, а внешнее поле в силу непрерывности тоже равно Н_СМ, составит с учетом соотношения (4.3)

G_N = F – HH_CM/(4) = F_N + H_CM²/(8) – H_CM²/(4) = F_S0 = G_S0. (4.22)

Определим поверхностную энергию границы раз­дела на единицу площади (рис. 4.1), как

Подставим в этот интеграл выражение (4.21) для G_S и воспользуемся формулой (4.5) для плотности свободной энергии сверхпроводника, выражая ее с учетом соотношений (4.2), (4.3) и (4.8) через безразмерный параметр порядка  = /₀:

получив окончательно:

.

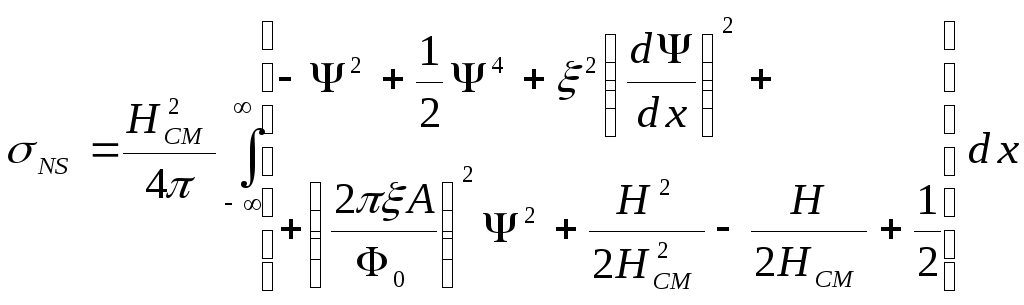С учетом формулы (4.20) имеем:

. (4.23)

Поскольку поле Н, проникшее в сверхпроводящий слой, всегда меньше поля Н_СМ (см. п. 3.1), второе слагаемое в квадратных скобках всегда отрицательное. Поэтому в теории Лондонов, не учи­тывающей квантовых эффектов, слагаемое ²(d/dx)² отсут­ствует и _NS < 0.

При переходе от нормальной области к сверхпроводящей параметр порядка  ме­няется от 0 до 1 на расстоянии порядка длины когерентнос­ти  (см.п.4.3), поэтому в области 0 < x <  можно принять ²(d/dx)² ~ 1, а вне этой области положить ²(d/dx)² = 0, то есть

.

Слагаемое же Н(Н – Н_СМ)/(2Н_СМ²) отлично от 0 и примерно равно 1 в области порядка глубины проникновения , поэтому

.

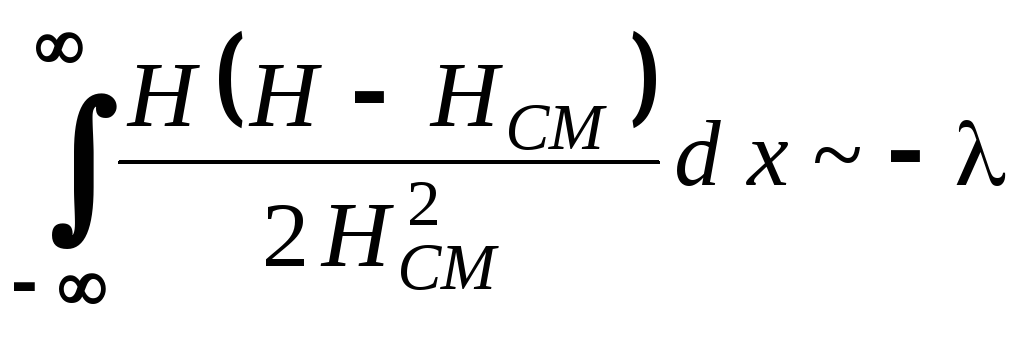Рис. 4.1. Потенциал Гиббса на границе раздела фаз Рис. 4.2. Сверхпроводник первого рода Рис. 4.3. Сверхпроводник второго рода

Рассмотрим два случая:

1)  << 1, то есть  <<  (рис. 4.2) тогда _NS ~ H_CM² > 0 – сверхпроводник первого ро­да. Точный расчет интеграла (4.23) по теории Гинзбурга – Ландау дает:

_NS = 1,89 H_CM²/(8). (4.24)

2)  >> 1, то есть  >>  (рис. 4.3) тогда _NS ~ –H_CM² < 0 – сверхпроводник второго рода. Точный расчет интеграла (4.23) по теории Гинзбурга – Ландау дает:

_NS = –H_CM²/(8). (4.25)

Точной границе между сверхпроводниками первого и второго рода соответствует .