12. Спектр элементарных возбуждений сверхпроводника.

Рассмотрим произвольную пару состояний (q, –q) в импульсном пространстве сверхпроводника и оценим вклад w_q, вносимый этой парой в полную энергию сверхпроводника. Из соотношения (6.6) видно, что

Первое слагаемое здесь - кинетическая энергия пары (q, –q), второе слагаемое учитывает, что рассматриваемая пара участвует во всех возможных взаимодействиях, при которых она переходит в произвольное состояние (К, –К), и наоборот, когда любые другие пары (К, –К) переходят в состояние (q, –q). Учитывая выражение (6.8) для ₀ и формулы (6.9) и (6.10) по­лучим:

Предположим теперь, что в основном состоянии сверхпроводника пара состояний (q, –q) заведомо пуста. Введем в сверхпроводник один добавочный электрон и поместим его в состояние q. Теперь уже пара (q, –q) не может участвовать в процессах рассеяния и вносить вклад в энергию основного состояния сверхпро­водника. Следовательно, энергия сверхпроводника с одним лишним электроном, то есть с элементарным возбуждением, составит:

, (6.16)

где E_q – кинетическая энергия добавленного электрона, W – энергия основного состояния сверхпроводника. То есть, добавляя один электрон к сверхпроводнику, находящемуся в основном состоянии, мы увеличиваем его энергию минимум на ₀. Иначе говоря, спектр элементарных возбуждений сверхпроводника отделен от основного состояния энергетической щелью ₀.

Из формулы (6.16) следует, что W_K – энергия элемен­тарного возбуждения с волновым вектором К, то есть величина, на которую увеличится энергия системы, если к сверхпровод­нику добавить электрон с волновым вектором К:

Эта зависимость приведена на рис. 6.4а. Найдем плотность состоя­ний элементарных возбуждений (W) = ddW, учитывая, что ddE = N(0):

. (6.17)

Эта зависимость приведена на рис. 6.4б.

Рис. 6.3. Функция рас­пределения электронов Рис.6.4. Энергия и плотность состояний

элементарных возбуждений в сверхпроводнике

Мы уже установили, что распределение спаренных электронов в К-пространстве описывается функцией v, которая (см. рис. 6.3) значительно меняется в области порядка K = 2₀K_F/E_F. Из соотношения неопределенностей следует, что область в трех­мерном пространстве, где волновая функция основного состояния сверхпроводника (то есть параметр порядка) сильно меняется, состав­ляет

Здесь v_F – фермиевская скорость, соответствующая кинетической энергии электрона, равной E_F. Эта величина x и является длиной когерентности в теории Гинзбурга – Ландау (см. п. 4.3). Таким образом:

. (6.18)

Если разорвать одну пару, то создадутся два элементарных воз­буждения, и на это потребуется энергия не меньше 2₀. Если k_BT ~ ₀, то под влиянием теплового возбуждения будет разорвано много пар и в К-пространстве много ячеек будет заполнено элементарными возбуждениями. Эти ячейки уже не будут участвовать во взаимных переходах и в формировании энергетической щели (6.8). Поэтому, чем выше температура, тем больше разорванных пар, тем меньше ширина энергетической щели. Соответственно ₀ в формуле (6.8) обозначает ширину энергетической щели при Т = 0.

Поскольку элементарные возбуждения подчиняются статистике Фер­ми – Дирака, вероятность заполнения состояния К_n одиночным электроном равна

Если хоть одно состояние К_n или –К_n заполнено, а вероят­ность этого равна 2f_n, то эта пара состояний уже не участвует во взаимодействиях. Следовательно, вероят­ность того, что пара (К, –К) участвует в создании сверхпроводящего состояния, равна 1 – 2f_n. Поэтому при Т > 0 формула (6.13) для энергии основного состояния сверхпроводника принимает вид:

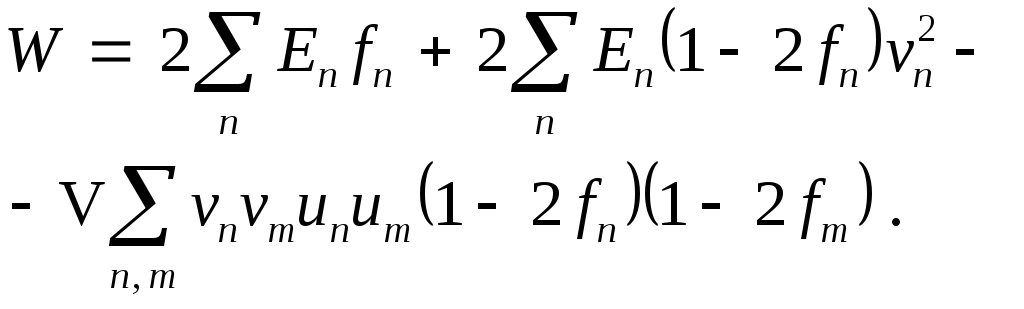
Здесь первое слагаемое – кинетическая энергия элементарных возбуждений, второе слагаемое – кинетическая энергия сверхпроводящих электронов, третье – энергия взаимодействия сверхпроводящих электронов через фононы. Условием равновесия является минимум свободной энергии системы F = W – TS. Пренебрегая зависимостью энтропии S от функции распределения v_n сверхпроводящих электронов по импульсам, из условия dF/dv_n = 0 получим:

, (6.19)

где обозначено

. (6.20)

Эта формула и определяет зависимость щели  от температуры. Из сравнения соотношений (6.20) и (6.8) видим, что (0) = ₀.

Запишем в соотношении (6.19) функцию v_n в виде, определенном формулой (6.10): , где. Тогда уравнение (6.20) с учетом соотношения (6.19) примет вид:

Переходя опять от суммирования к интегрированию, после несложных преобразований получим:

. (6.21)

Это уравнение в неявном виде определяет зависимость (Т), которая изображена на рис. 6.5. Поскольку при исчезновении щели пропадает и сверхпроводимость, критическую температуру можно определить из условия (Т_С) = 0. Подставляя в соотношение (6.21)  = 0 и Т = Т_С, получим уравнение относительно критической температуры Т_С:

.

Проведя интегрирование, получаем:

. (6.22)

Подставляя сюда из соотношения (6.12) , получим:

. (6.23)

Заметим, что формула (6.22) дает объяснение изотоп-эффекта. Действительно, поскольку (модель шариков на пружинах), сразу получаем:Т_СМ^1/2 = const.