Первое критическое поле

Найдём первое критическое поле H_C1, при котором впервые становится энергетически выгодным существование вихря внутри сверхпроводника второго рода. Рассмотрим вновь случай  >> , то есть типично лондоновский случай, когда поправки за счет  несущественны, и можно воспользоваться лондоновским выражением для свободной энергии сверхпроводника в магнитном поле (см. п. 2.2). Энергия на единицу длины вихревой нити, отсчитанная от уровня энергии сверхпроводника без вихрей, равна

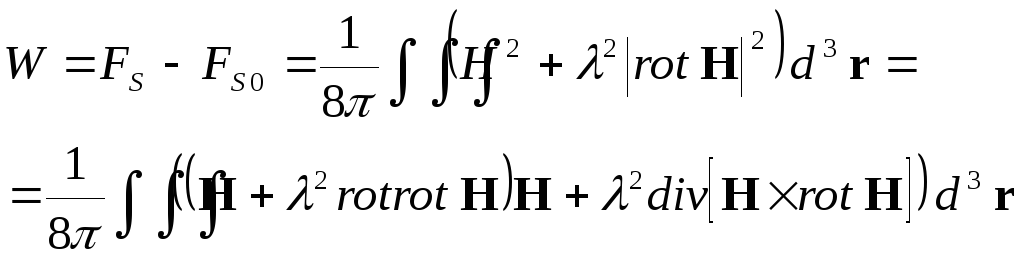
Здесь мы воспользовались соотношением arot b = brot a ­– div [ab], ин­теграл берется по пространству, заключенному между двумя бесконечными параллельными плоскостями, перпендикулярными вихревой нити и отстоящими на единичное расстояние друг от друга, то есть плоскостями z = 0 и z =1. По теореме Гаусса

Поскольку вектор Н направлен вдоль оси вихря, то есть вдоль оси z и перпендикулярен плоскостям z = 0 и z =1, то вектор Hrot H лежит в этих плоскостях, и подынтегральное выражение на этих плоскостях равно нулю. С другой сто­роны, H()=0, поэтому

,

и с учетом уравнений (5.1) и (5.3) получаем:

(5.4)

Однако мы еще не учли, что сердцевина вихря находится в нормальном состоянии и ее плотность свободной энергии выше, чем в окружающей сверхпроводящей среде на величину F_N – F_S0 = H_CM²/(8), как это следует из формулы (1.2). Соответственно дополнительная энергия на единицу длины нити равна H_CM²²/8. Используя формулу (4.19), можно положить:

.

Поскольку энергия одиночного вихря в сверхпроводнике положительна, в отсутствие внешнего магнитного поля вихрю энергетически не выгодно оставаться внутри сверхпроводника. Условия равновесия сверхпроводника во внешнем постоянном магнитном поле Н₀ – минимум потенциала Гиббса

, (5.5)

поскольку вихрь несет один квант магнитного потока. В магнитном поле Н₀ > H_C1 = 4W/Ф₀ потенциал Гиббса становится отрицательным, то есть существование вихря становится энергетически выгодно. Из соотношений (5.4) и (5.5) получаем:

, (5.6)

то есть примерно в 2 раза меньше, чем поле внутри вихря (см. 5.3). Если

 = 100, Н_СМ = 10³ Э, то Н_С1 = 30 Э.

9. Взаимодействие вихрей, второе критическое поле сверхпроводника II рода. Сверхпроводимость второго рода

Теория Гинзбурга – Ландау была развита в 1957 г. А.А. Абрикосовым, который дал последовательное феноменологическое описание сверхпроводников второго рода и объяснил такие их свойства, как сложное поведение в магнитном поле, огромные критические поля сверхпроводящих сплавов. Как отмечалось в п. 1.2 в сверхпроводники второго рода внешнее магнитное поле Н₀ не проникает вплоть до первого критического поля Н_С1 (рис.5.1). При поле Н_С1 < Н₀ < Н_С2 внутри сверх­проводника появляется магнитное поле в виде квантовых вихревых нитей. Каждая такая нить, или вихрь, имеет нормальную сердцевину радиусом порядка , параметр порядка  в которой равен нулю. Вокруг этой сердцевины течет незатухающий сверхпроводящий ток, ориентированный так, чтобы создаваемое им магнитное поле было направлено вдоль нормальной сердцевины и совпадало по направлению с внешним магнитным полем.

Сверхпроводящий вихревой ток охватывает область радиусом порядка  >> . Один такой вихрь несет магнитный поток, равный одному кванту потока Ф₀, проникшие в сверхпроводник вихри образуют в поперечном сечении правильную треугольную решетку, то есть возникает смешанное состояние. Возникнув в магнитном поле Н_С1, вихревая решетка существует и в более сильных внешних полях, при этом с ростом внешнего поля плотность вихрей увеличивается. Наконец, в поле Н_С2 расстояние между центрами ближайших вихрей становится меньше 2, то есть нормальные сердцевины сливаются, и параметр порядка становится равным нулю во всем объеме сверхпроводника – происходит фазовый переход второго рода в нормальное состояние.

Рассмотрим пару параллельных однонаправленных вихрей в безгра­ничном сверхпроводнике. Пусть, как и раньше,  >> 1. Пока расстояние между вихрями много больше размера области вихревых токов , вихри "не чувствуют" друг друга. Но если расстояние между вихрями стало меньше , то сердцевина одного вихря оказывается в области сверхтоков второго вихря, и наоборот. Пусть координаты центров вихрей r₁ и r₂ соответственно. Энергия системы двух вихрей, отсчитанная от энергии сверхпроводника без вихрей, в соответствии с соотношениями (5.1) и (5.4) равна:

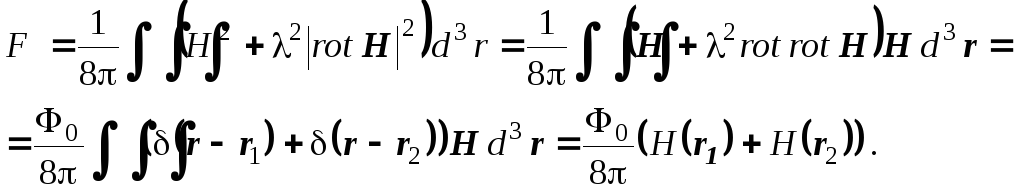
Поле Н(r₁) – это магнитное поле в центре первого вихря. Оно состоит из поля Н(0), создаваемого самим вихрем в своем центре, и из поля Н₁₂(х), создаваемого там вторым вихрем, отстоящим от первого на расстоянии х = |r₁ – r₂|. То же самое можно ска­зать и о втором поле Н(r₂). Тогда:

F = 2W + 2H₁₂(x)Ф₀/(8),

где W – энергия одиночного вихря, определенная формулой (5.4). Второе слагаемое здесь, по сути, – энергия взаимодействия вихрей, то есть

U(x) = Ф₀H₁₂(x)/(4). (5.7)

Сила взаимодействия между вихрями на единицу длины вихря составляет:

,

где j₁₂ – плотность тока, наводимого вторым вихрем в точке, где находится центр первого вихря. Одинаково направленные вихри при этом отталкиваются. В общем случае, если вихрь обтекается каким-то сторонним током j, то на единицу его длины действует сила, называемая силой Лоренца:

. (5.8)

Взаимодействие вихрей позволяет понять очень интересное явление – перегрев мейсснеровского состояния. Рассмотрим идеально гладкую поверхность сверхпроводника и одиночный вихрь вблизи ее на расстоянии х₀. Поскольку  >> 1, магнитное поле, создаваемое вихрем, удовлетворяет линейному уравнению (5.1), а на поверхности сверхпроводника равно нулю, как магнитное поле вне длинного соленоида. Для линейных задач справедлив принцип суперпозиции, и в силу единственности эта задача эквивалентна безграничному сверхпроводнику с двумя противоположно направленными вихрями, расположенными в точках с координатами х₀. Эти вихри будут притягиваться, то есть вихрь притягивается к поверхности сверхпроводника, причем, чем ближе вихрь к поверхности, тем больше притяжение.

Эту отрицательную энергию взаимодействия с поверхностью, со­от­ветствующую притяжению, следует добавить в формулу (5.5) для потенциала Гиббса одиночного вихря в безграничном сверхпроводнике. В результате потенциал Гиббса обратится в нуль во внешнем магнитном поле, меньшем, чем Н_С1. Иными словами, существование вихря в сверхпроводнике вблизи границы будет энергетически выгодно даже во внешнем поле, меньшем, чем Н_С1. Можно сказать, что вблизи поверхности су­ществует потенциальный барьер Бина – Ливингстона, препятствующий выходу вихря. Аналогично, если внешнее поле Н₀ увеличивается от нуля, то вихрю энергетически выгодно проникнуть внутрь сверхпроводника при Н₀ = Н_С1, но его "не пускает" барьер Бина – Ливингстона. Таким образом, во внешних полях Н₀ > Н_С1 продолжает существовать, но уже метастабильно, мейсснеровское состояние. Лишь во внешнем магнитном поле Н₀ = Н_П, называемом полем перегрева, вихрь сможет преодолеть барьер и проникнуть вглубь сверхпроводника. Точный расчет показывает, что

Н_П = Н_СМ для очень гладкой поверхности сверхпроводника.