
- •1. Введение
- •Термодинамическая система и термодинамические параметры
- •2. Основные принципы статистики
- •2. 1. Статистическое распределение
- •Фазовый объем и его свойства
- •Плотность функции распределения
- •Свойства плотности функции распределения
- •2.2. Теорема Лиувилля
- •2.3. Микроканоническое распределение
- •Особенности квантовой статистики
- •2.4. Статистический вес. Энтропия
- •а) Квантовая статистика
- •б) Классическая статистика
- •2.5. Связь энтропии с функцией распределения
- •Квантовое рассмотрение
- •Классический случай
- •3. Термодинамические величины. Температура. Адиабатический процесс. Давление. Работа и количество тепла.
- •3.1. Температура
- •Определение температуры
- •Положительность температуры
- •Установление теплового равновесия
- •3.2. Давление
- •Адиабатический процесс
- •Определение давления.
- •Условие механического равновесия
- •3.3. Внутренняя энергия системы, работа и теплота.
- •4. Термическое и калорическое уравнение состояния. Первое и второе начало термодинамики. Теплоемкость.Термодинамические потенциалы. Метод ТД потенциалов.
- •4.1. Термические и калорическое уравнения состояния
- •4.2. Уравнение первого начала термодинамики
- •4.3. Теплоемкость
- •4.4. Второе начало термодинамики
- •4.5. Термодинамические потенциалы
- •5. Основные термодинамические процессы и их уравнения
- •5.1. Политропные процессы
- •5.2. Термодинамические коэффициенты
- •5.3. Второе начало для неравновесных процессов. Основное уравнение и основное термодинамическое неравенство.
- •5.4. Цикл Карно. Теоремы Карно.
- •6. Третий закон термодинамики и его следствия
- •6.1. Теорема Нернста.
- •7. Зависимость термодинамических величин от числа частиц.
- •7.1. Химический потенциал. Большой термодинамический потенциал
- •7.2. Условия равновесия и устойчивости термодинамических систем
- •Общие условия термодинамического равновесия и устойчивости
- •Условие устойчивости равновесия однородной системы
- •Принцип Ле Шателье — Брауна
- •8. Фазовые переходы
- •8.1. Условия равновесия фаз
- •8.2. Правило фаз Гиббса
- •8.3. Фазовые переходы первого рода
- •8.4. Фазовые переходы второго рода
Термодинамика и статфизика часть 1 |
28 |
С определением теплоемкости тесно связано понятие о термостате, которое широко используется в термодинамике. Термостат — тело с настолько большой теплоемкостью (С®µ), что его температура при теплообмене с какой-либо системой не изменяется. Когда говорят о системе, помещенной в термостат, то имеют в виду систему, в которой при всех происходящих в ней процессах (расширение, намагничивание и т. д.) температура поддерживается постоянной.
. Очевидно, что теплоемкость тела зависит, во-первых, от его массы, а во-вторых, от того, в каких условиях происходит процесс нагревания. Впредь, говоря о теплоемкости, мы всегда будем иметь ввиду мольную теплоемкость, т.е. теплоемкость одного моля вещества. Что касается зависимости теплоемкости от условий нагревания, то обычно
приходиться иметь дело с теплоемкостью при постоянном объеме CV и теплоемкостью при постоянном давлении CP . Первая из них называется изохорной, а вторая изобарной:
|
æ |
¶ Q ö |
æ |
¶ S ö |
|
|
CV = |
ç |
÷ |
= T ç |
|
÷ |
; |
|
||||||
|
è |
¶ T ø V |
è |
¶ T ø V |
|
|
|
æ |
¶ Q ö |
æ |
¶ S ö |
|
|
|
CP = |
ç |
÷ |
= T ç |
|
÷ |
; |
(4.2) |
|
|||||||
|
è |
¶ T ø P |
è |
¶ T ø P |
|
|
|
Разумеется, нагревание системы может происходить в условиях, когда и давление, и объем системы изменяются. Соответствующие теплоемкости не будут совпадать ни с CV
, ни с CP . Замечу, что теплоемкость является одной из наиболее часто измеряемых
тепловых характеристик тел. Это связано с тем, что, будучи макроскопической характеристикой тела, теплоемкость непосредственно связана со структурой тела на микроуровне. Вспомните, изохорная теплоемкость идеального газа просто пропорциональна числу степеней свободы молекул этого газа. То есть, измерив количество тепла, необходимое для нагревания газа на один градус, мы можем сказать, как устроена его молекула.
4.4. Второе начало термодинамики
Первое начало термодинамики, как мы видели, устанавливает существование у всякой системы однозначной функция состояния — внутренней энергии, которая не изменяется в отсутствие внешних воздействий при любых процессах внутри системы.
Второе начало термодинамики устанавливает существование у всякой равновесной системы другой однозначной функции состояния — энтропии, которая, однако, в отличие от внутренней энергии не изменяется у изолированной системы только при равновесных процессах и всегда возрастает при неравновесных процессах; аналогично ведет себя энтропия у адиабатных систем.
Таким образом, если первое начало есть закон сохранения и превращения энергии (его количественная сторона) в применении к термодинамическим системам, то второе начало представляет собой закон об энтропии.
Общая характеристика и исходная формулировка второго начала
Открытие второго начала связано с анализом работы тепловых машин, чем и определяется его исходная формулировка.
Так же, как и первое начало, второе начало термодинамики является обобщением данных опыта. В результате анализа этих закономерностей было сформулировано второе начало в виде закона о существовании энтропии и ее неубывании при любых процессах в
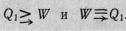
Термодинамика и статфизика часть 1 |
29 |
изолированных (или только адиабатически изолированных) системах.
Для того чтобы лучше понять второй закон термодинамики рассмотрим особенности превращения теплоты в работу и работы в теплоту.
Мы уже обсуждали, что понятия теплота и работа - две формы передачи энергии не являются равноценными: в то время как работа A может непосредственно пойти на увеличение любого вида энергии, теплота Q непосредственно, без предварительного превращения в работу, приводит лишь к увеличению внутренней энергии системы.
Как показывает опыт, превращение работы в теплоту может происходить при контакте двух тел (например, при нагревании посредством трения).
при преобразовании теплоты в работу наряду с охлаждением Для преобразования теплоты в работу необходимо три тела нагреватель, рабочее тело и
холодильник. Отдача части теплоты рабочим телом холодильнику называется компенсацией. Результаты опытов показывают, что без компенсации ни один джоуль теплоты в работу превратить нельзя. В то же самое время работа в теплоту превращается полностью без всякой компенсации.
Такая неравноправность превращениятеплоты в работу по сравнению с превращением работы в теплоту приводит к односторонности естественных процессов: самопроизвольные процессы в замкнутой системе идут в направлении исчезновения потенциально возможной работы. При тепловом контакте двух тел различной температуры теплота переходит от горячего тела к холодному до тех пор, пока их температуры не станут равными.
Устройство, которое без компенсации полностью превращало бы периодически в работу теплоту какого-либо тела, вечным двигателем второго рода.
Формулировка второго Начала, выражающая закономерности превращения теплоты в работу и работы в теплоту следующая: невозможен вечный двигатель второго рода.
Второе начало термодинамики представляет собой совокупность двух независимых положений:
Совместно первое и второе положения второго начала устанавливают односторонний характер изменения энтропии при естественных процессах в замкнутых системах.
Второе начало термодинамики, допускает большое число различных, но эквивалентных формулировок. Например формулировки Карно, Клаузиуса, Кельвина, Оствальд, которые сводятся к следующим:
а) невозможно перевести тепло от менее нагретого тела к более нагретому телу без какихлибо иных изменений в природе:
б) невозможно тепло, отнятое от некоторого тела, нацело превратить в работу без каких-либо иных изменений в природе; в) невозможно построить вечный двигатель второго рода.
В применении к равновесным процессам любая из этих эквивалентных формулировок приводит к существованию функции состояния системы (энтропии), связанной с количеством тепла соотношением
δQ = TdS

Термодинамика и статфизика часть 1 |
30 |
С учетом этого получим совместную запись I и II начал термодинамики в виде основного термодинамического тождества
dU = TdS-PdV.
Основное уравнение термодинамики для равновесных процессов. Связь между термическим и калорическим уравнениями состояния
Основное уравнение термодинамики для равновесных процессов TdS = dE + å Fi dai (7)
Уравнение является исходным при анализе всех равновесных процессов в термодинамических системах с постоянным числом частиц.
Как мы отмечали, при вычислении многих величин необходимо знать как термическое, так и калорическое уравнения состояния системы. Экспериментально эти уравнения могут быть получены независимо друг от друга. Уравнение (7) позволяет установить дифференциальную связь между ними, которая в некоторых случаях делает ненужным знание или калорического уравнения состояния, или только зависимости внутренней энергии от внешних параметров. Действительно, из основного уравнения термодинамики находим
откуда, подобно можно получить дифференциальное уравнение, связывающее термическое и калорическое уравнения состояния:
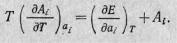 (8)
(8)
Для простой системы F=Р, a=V, уравнение (8) имеет вид
Для идеального газа термическим уравнением состояния является уравнение Клапейрона— Менделеева
PV=RT.
Из этого уравнения (dP/dT)v=R/V. Подставляя найденное выражение производной {dP/dT)v в формулу (8), получаем закон Джоуля
(dE/dV)T=0,
который, как мы уже показывали, позволяет найти калорическое уравнение состояния газа, если дополнительно известнатемпературная зависимость его теплоемкости:
E = ò CvdT.
Для одноатомного идеального газа с точностью до аддитивной постоянной имеем E = CVT
4.5. Термодинамические потенциалы
Уравнение (4.1), записанное в виде
Термодинамика и статфизика часть 1 |
31 |
d E = T d S − P d V
означает, что внутренняя энергия E является однозначной функцией энтропии системы S и объема V . Зная E как функцию от S и V , можно найти температуру и давление системы, которые, разумеется, также являются функциями от энтропии и объема:
æ |
¶ E ö |
, |
æ |
¶ E ö |
(4.3) |
T ( S,V ) = ç |
÷ |
P ( S,V ) = - ç |
÷ |
||
è |
¶ S ø V |
|
è |
¶ V ø |
S |
Использование энтропии в качестве термодинамической переменной чаще всего неудобно, так как не существует приборов, измеряющих эту величину. Единственным исключением является случай, когда мы имеем дело с теплоизолированной системой. Переход к другим переменным осуществляется с помощью, так называемых, преобразований Лежандра. Покажем, как работают преобразования Лежандра и, одновременно, введем другие возможные функции состояния, которые используются при описании однокомпонентных систем
а) Свободная энергия (переменные T и V )
Добавим и вычтем в правой части уравнения (4.1) член S dT .
|
d E = T d S − P d V + S dT − S dT . |
|
Учитывая, что |
S dT + T dS = d ( T S ) , получаем |
|
|
d E−TS =dF=−SdT −PdV |
(4.4) |
Комбинация |
величин F = E − T S называется свободной |
энергией системы или |
энергией Гельмгольца. Ее изменение при переходе системы из одного состояния в другое, также как изменение энергии ( E ), не зависит от способа перехода, а определяется только самими этими состояниями - свободная энергия F является функцией состояния. Тот факт, что в правой части уравнения (4.4), определяющего изменение свободной энергии, под знаками дифференциалов стоят температура и объем системы, означает, что свободная энергия является функцией состояния в переменных T и V . Зная зависимость свободной энергии F от температуры и объема, из уравнения (4.4) непосредственно находим:
æ |
¶ F ö |
|
æ |
¶ F ö |
|
æ |
¶ S ö |
æ |
¶ 2 F |
ö |
æ |
¶ P ö |
|
S ( T ,V ) = - ç |
÷ |
, |
P ( T,V ) = - ç |
÷ |
; |
ç |
|
÷ |
= ç |
|
÷ |
= ç |
÷ |
|
|
||||||||||||
è |
¶ T ø V |
|
è |
¶ V ø T |
|
è |
¶ V ø T |
è |
¶ V¶ T ø |
è |
¶ T øV |
||
(4.5)
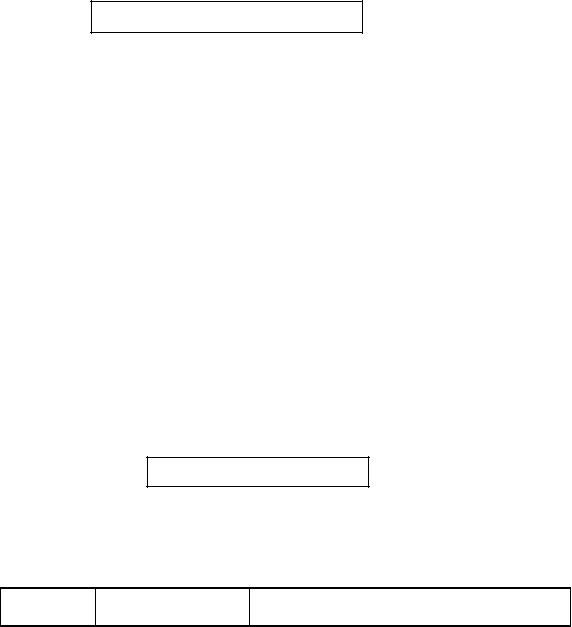
Последние соотношения решают одну из важнейших задач физики конденсированного состояния: определение уравнения состояния системы. Дело за малым: надо знать зависимость свободной энергии от температуры и объема системы. Вычисление явной зависимости свободной энергии от температуры и объема, является одной из основных задач статистической физики. А вот вычисление различных физических величин после того, как свободная энергия найдена, либо установление связей между этими величинами, является уже основной задачей термодинамики. В частности, из определения изохорной теплоемкости, находим
Термодинамика и статфизика часть 1 |
|
|
|
|
|
|
|
|
32 |
|
|
æ |
¶ |
S ö |
|
æ |
¶ 2 F ö |
||||
CV |
= T ç |
|
|
÷ |
= - T |
ç |
¶ T |
2 |
÷ |
|
¶ |
|
|||||||||
|
è |
T ø V |
|
è |
|
ø V |
||||
б) Потенциал Гиббса (переменные T и P )
Перепишем уравнение (4.4) в виде
d ( E - T S ) = d F = - S dT - P dV - V dP + V dP
В соответствии с общим правило, по которым выполняются преобразования Лежандра, мы добавили и вычли в правой части уравнения (4.4) член V dP . Учитывая, что
P dV + V dP = d ( PV ) , получаем:
d (E − T S + PV ) ≡ d Φ = − S dT + V dP
Комбинация |
F ( T , P) = E - T S + PV называется термодинамическим потенциалом |
системы или потенциалом Гиббса. Потенциал Гиббса является функцией состояния в переменных T и P .
æ |
¶ F |
ö |
|
|
æ |
¶ F |
ö |
|
S ( T , P) = - ç |
|
÷ |
, |
V ( T, P) = |
ç |
|
÷ |
; |
|
|
|||||||
è |
¶ T ø P |
|
|
è |
¶ P ø T |
|
||
æ |
¶ S ö |
æ |
¶ 2 F |
ö |
|
|
æ |
¶ V ö |
||
ç |
|
÷ |
= - ç |
|
|
÷ |
= |
- |
ç |
÷ |
|
¶ P¶ |
|
||||||||
è |
¶ P ø T |
è |
T ø |
|
|
è |
¶ T ø P |
|||
Итак, мы имеем три функции состояния:
-внутренняя энергия ( переменные S и V );
1.потенциал Гельмгольца (переменные T и V );
2.потенциал Гиббса (переменные T и P );
в) Энтальпия
Введем, наконец, последнюю функцию состояния – энтальпию. Вернемся к уравнению (4.1). Добавим и вычтем в правой части этого уравнения член P d V
d E = T d S − P d V − V dP + V dP
После переноса членов P d V + V dP = d ( PV ) в левую часть этого уравнения, получаем
d ( E + PV ) ≡ dW = T d S + V dP
Функция W ( S, P) = E + PV является функцией состояния в переменных S и P , и
называется энтальпией.
Приведем сводную таблицу полученных функций состояния:
Функция |
дифференциал |
Первые производные |
|
состояния |
|||
|
|
||
|
|
|
Термодинамика и статфизика часть 1 |
|
|
|
|
|
|
|
|
|
|
|
|
33 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия |
d E = T dS − P dV |
T ( S,V ) = |
æ |
¶ |
E ö |
; P( S,V ) = - |
|
æ |
¶ |
E ö |
|
|
||||||
|
E ( S,V ) |
ç |
¶ |
÷ |
|
ç |
¶ |
V |
÷ |
|
|
||||||||
|
|
|
|
|
|
|
è |
S ø V |
|
|
|
|
è |
ø S |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Энтальпия |
d W = T dS + V dP |
T ( S, P) = |
æ |
¶ W ö |
; V ( S, P) = |
|
æ |
¶ W |
ö |
|
|
|||||||
|
W ( S, P) |
ç |
|
÷ |
|
ç |
|
¶ |
P |
÷ |
|
|
|||||||
|
|
|
|
|
|
è |
¶ S ø P |
|
|
è |
|
ø S |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свободная |
d F = |
− |
S dT − P dV |
S ( T ,V ) = |
|
æ |
¶ F |
ö |
; P ( T,V ) |
= |
|
|
æ |
¶ |
F |
ö |
|
|
|
энергия |
- ç |
¶ T |
÷ |
|
- ç |
¶ |
V |
÷ |
|
|||||||||
|
F ( T ,V ) |
|
|
|
|
|
|
è |
ø V |
|
|
|
|
è |
ø T |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенциал |
d Φ = |
− |
S dT + V dP |
S ( T , P) = |
|
æ |
¶ F |
ö |
; V ( T, P) |
= |
|
æ |
¶ F |
ö |
|
|
||
|
Гиббса |
- ç |
¶ T |
÷ |
|
ç |
¶ |
|
÷ |
|
|
||||||||
|
F ( T , P) |
|
|
|
|
|
|
è |
ø P |
|
|
|
è |
P ø T |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание: Внутренняя энергия Е в переменных S и V называется также |
|
|
|
|
|
|
|
|
|||||||||||
термодинамическим потенциалом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Это название связано с тем, что значение давления выражается через внутреннюю энергиию
P = |
æ |
¶ E ö |
|||
- ç |
|
÷ |
|||
¶ V |
|||||
|
è |
|
ø S |
||
по аналогии с механикой, где сила выражается через потенциальную энергию U |
|||||
F = |
- |
∂ U |
|
|
|
|
|
|
|||
x |
|
¶ x |
|
|
|
|
|
|
|
||
Математическое отступление (о якобианах)
Существуют простые формальные правила, которые позволяют получать любые соотношения между термодинамическими производными
Из четырех величин - объема, давления, температуры и энтропии – в качестве независимых переменных используются только такие комбинации: {энтропия – объем},
{энтропия – давление}, |
{температура – объем} и {температура – давление}. |
И ни разу не |
использовали в качестве |
независимых переменных такие комбинации как |
{энтропия – |
температура} или {объем – давление}. Это запрещено. Чтобы понять, откуда взялся этот
запрет, взгляните на последний столбец сводной таблицы функций состояния. |
Обратите |
||||||
внимания |
на то, |
что |
энтропия и |
температура связаны друг с другом |
простыми |
||
соотношениями: |
|
|
|
|
|
|
|
T ( |
S,V ) = |
æ |
¶ E ö |
или S ( T ,V ) |
æ |
¶ F ö |
|
ç |
÷ |
= - ç |
÷ . |
|
|||
|
|
è |
¶ S ø V |
|
è |
¶ T ø V |
|
Совершенно аналогичная ситуация имеет место с давлением и объемом. Величины, которые выражаются друг через друга таким образом, называются термодинамически сопряженными величинами. Очевидно, что термодинамически сопряженные величины, будучи связаны друг с другом дифференциальными соотношениями, не могут выступать в качестве независимых переменных.
Так вот, формальные правила перехода справедливы только в случае перехода от одних независимых переменных к другим.
Введем новое определение.
Рассмотрим две произвольные функции u( x, y) и v( x, y) .
∂ ( u,v)
Якобианом ∂ ( x, y) называется определитель:

Термодинамика и статфизика часть 1
¶(( u,v)) =
¶x, y
æ |
¶ |
u ö |
, |
æ |
¶ |
u ö |
||
ç |
|
|
÷ |
ç |
|
|
÷ |
|
¶ |
|
¶ |
|
|||||
è |
x ø y |
è |
y ø x |
|||||
æ |
¶ |
v ö |
, |
æ |
¶ |
v ö |
||
ç |
|
|
÷ |
ç |
|
|
÷ |
|
¶ |
|
¶ |
|
|||||
è |
x ø |
y |
è |
y ø x |
||||
= |
æ |
¶ |
u ö |
æ |
¶ |
v ö |
- |
||
ç |
|
|
÷ |
ç |
|
|
÷ |
||
¶ |
|
¶ |
|
||||||
|
è |
x ø |
y è |
y ø x |
|
||||
34
æ |
¶ |
u ö |
æ |
¶ |
v ö |
||
ç |
|
|
÷ |
ç |
|
|
÷ |
¶ |
|
¶ |
|
||||
è |
y ø |
x è |
x ø y |
||||
Расписывая якобианы в виде определителей, легко непосредственно убедиться в том, что для якобианов справедливы следующие правила:
|
|
|
|
|
|
∂ ( u,v) |
= |
− |
∂ ( v,u) |
, а также |
∂ ( u,v) |
= |
∂ ( u,v) |
|
∂ ( t, z) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∂ ( x, y) |
∂ ( |
x, y) |
∂ ( x, y) |
∂ ( t, z) |
∂ ( x, y) |
||||||||||||||
Основные правила применения якобианов |
|
|
|
|
|||||||||||||||||||||
Термодинамический потенциал |
|
|
|
|
|
|
|
||||||||||||||||||
dE=TdS-PdV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
является полным дифференциалом. Из этого следует |
|
|
|||||||||||||||||||||||
æ |
|
¶ E |
ö |
|
|
|
|
æ |
|
¶ E |
ö |
|
|
|
|
|
|
|
|
|
|
||||
T = ç |
|
|
÷ |
|
P = |
|
- ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
|
|
|||||
|
¶ S |
|
|
¶ V |
|
|
|
|
|
|
|
|
|||||||||||||
è |
|
ø |
V |
|
è |
|
ø |
S |
|
|
|
|
|
|
|
|
|||||||||
æ ¶ T |
ö |
= |
|
|
¶ 2 E |
|
|
æ |
|
¶ P ö |
= - |
¶ 2 E |
|
|
|
|
|
||||||||
ç |
|
|
÷ |
|
|
|
|
, |
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
||||
|
|
|
|
¶ V¶ S |
|
|
|
|
¶ S¶ V |
|
|
|
|
|
|||||||||||
è ¶ V |
ø |
S |
|
|
|
|
è |
|
¶ S ø V |
|
|
|
|
|
|
||||||||||
поскольку порядок взятия производных можно поменять, то
æ |
¶ T ö |
æ |
¶ P ö |
|
||
ç |
|
÷ |
= - ç |
|
÷ |
(1). |
|
|
|||||
è |
¶ V ø S |
è |
¶ S ø |
V |
||
Теперь давайте перепишем (1) в форме якобианов Для этого частные производные представим в виде якобианов
æ |
¶ T ö |
= |
¶ (T, S) |
, |
æ |
¶ P ö |
= |
¶ (P,V ) |
|||||||||
ç |
|
|
÷ |
|
|
|
|
|
ç |
|
÷ |
|
|
||||
|
|
¶ |
(V , S) |
|
¶ (S,V ) |
||||||||||||
è |
¶ V ø S |
|
|
è |
¶ S ø V |
|
|||||||||||
и тогда (1) примет вид |
|
|
|
|
|
||||||||||||
|
∂ (T, S) |
= - |
|
∂ (P,V ) |
|
|
|
|
|
|
|||||||
|
¶ (V , S) |
|
|
|
|
¶ (S,V ) |
|
|
|
|
|
|
|||||
|
∂ (T, S) |
= - |
|
|
∂ (V , S) |
= 1 |
|
|
|
|
|
||||||
|
¶ (P,V ) |
|
|
|
|
¶ (S,V ) |
|
|
|
|
|
|
|||||
|
|
|
∂ (T, S) |
|
= 1 |
|
|
|
|
|
|
|
|
|
(2) |
||
|
|
|
∂ (P,V ) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
последняя формула играет важную роль в термодинамике и мы ее будем периодически использовать.
В термодинамике часто ставят задачу выразить плохо измеримые на опыте коэффициенты через хорошо измеримые. При этом плохо измеримыми коэффициентами обычно называют все, содержащие энтропию S.
Это связано с тем, что в экспериментальной физике имеются различные типов манометров, термометров, но нет приборов измеряющих энтропию непосредственно.
Возникает задача об исключении энтропии из якобианов. Для ее решения можно
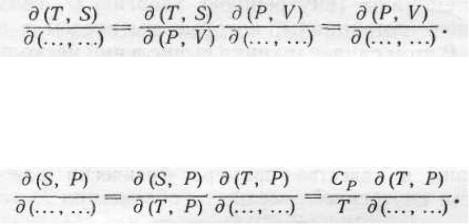
Термодинамика и статфизика часть 1 |
35 |
сформулировать три правила.
1.Если в якобиане энтропия стоит в паре с температурой, то в силу основного термодинамического тождества
2.Если энтропия стоит в паре с объемом, то
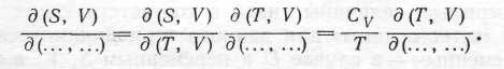 (7) 3. Если энтропия стоит в паре с давлением
(7) 3. Если энтропия стоит в паре с давлением
Якобианы и приведенные для них очень простые правила оказываются чрезвычайно эффективными в термодинамике при переходе от одних переменных к другим. Продемонстрируем их работу на примере перехода от одной теплоемкости к другой.
а) Рассмотрим переход от изохорной теплоемкости CV к изобарной теплоемкости CP
без использования якобианов.
Мы с вами уже получали выражение для этих теплоемкостей, я еще раз напомню
C = |
|
δ Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
¶ T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
CV |
= |
|
(δ Q)V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
¶ T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
CP |
= |
|
(δ Q)P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
¶ T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку dS=dQ/T, то |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
(δ Q)V |
|
æ ¶ S ö |
|
|
|
|
|
(δ Q)P |
æ |
¶ S ö |
|||||||||||||||||
CV |
= |
|
|
|
|
|
|
|
|
|
= Tç |
|
|
|
|
÷ |
|
, |
|
CP = |
|
|
|
= Tç |
|
÷ |
|||||
|
|
|
|
¶ T |
|
|
|
|
|
|
|
|
¶ T |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è ¶ T ø V |
|
|
|
|
|
|
è |
¶ T ø P |
|||||||||||||
Согласно первому закону термодинамики |
|
|
|||||||||||||||||||||||||||||
dQ=dE+PdV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||
E=E(T,V) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
æ |
|
¶ E |
ö |
|
|
|
æ |
|
¶ E |
ö |
|
|
|
|
|
|
|
|
|
|
|
|||||||
dE = |
ç |
|
|
|
|
÷ |
|
|
dT + ç |
|
|
|
÷ |
|
dV |
|
|
|
|
|
|
|
|
||||||||
|
¶ T |
|
|
|
¶ V |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
è |
|
ø |
V |
è |
|
ø T |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
æ |
¶ E |
ö |
|
|
|
é æ |
|
¶ E |
ö |
|
ù |
|
|
|
|
|
|
|
|
|||||||||
δ Q |
= |
|
ç |
|
|
|
÷ |
|
|
dT |
+ ê ç |
|
|
|
|
÷ |
|
+ Pú |
dV |
(1a) |
|
|
|||||||||
|
¶ T |
|
|
|
¶ V |
|
|
|
|||||||||||||||||||||||
|
|
|
è |
ø V |
|
ë è |
|
ø T |
û |
|
|
|
|
|
|
|
|
||||||||||||||
поскольку при V=const dV=0, то |
|
|
|
|
|
|
|||||||||||||||||||||||||
CV |
= |
|
æ |
¶ E |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||||
|
¶ T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
è |
ø V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
(δ Q)P |
|
|
æ |
¶ E ö |
|
|
|
é |
æ |
¶ E ö |
|
|
ù æ |
¶ V ö |
|
|
|||||||||||
CP |
= |
|
|
|
|
¶ T |
|
|
|
|
= ç |
|
÷ |
|
+ |
|
ê |
ç |
|
÷ |
|
+ |
Pú ç |
|
÷ |
(2а) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
¶ T ø |
V |
ë |
è |
¶ V ø |
T |
|
û è |
¶ T ø P |
|
|
||||||||||
или

Термодинамика и статфизика часть 1 |
36 |
||||||
é æ |
¶ E ö |
|
ù æ ¶ V ö |
||||
CP = СV + ê ç |
|
÷ |
+ |
Pú ç |
|
|
÷ |
|
|
|
|||||
ë è |
¶ V ø T |
|
û è |
|
¶ T ø P |
||
Нам удобнее будет получить другое соотношение для СР. Если считать независимыми переменными T и P V=V(T,P)
æ |
|
¶ V ö |
|
|
æ |
|
¶ V ö |
|
|||||
dV = ç |
|
|
|
|
÷ |
|
dT + |
ç |
|
|
|
÷ |
dP |
|
¶ T |
|
|
¶ P |
|||||||||
è |
|
ø |
P |
|
è |
|
ø |
T |
|||||
æ |
¶ E ö |
|
|
æ |
|
¶ E ö |
|
|
|||||
dE = ç |
|
÷ |
|
dT + ç |
|
|
÷ |
|
dP |
||||
|
|
|
|
|
|||||||||
è |
¶ T ø |
|
P |
è |
|
¶ P ø T |
|
||||||
тогда соотношение (1) перепишется в виде
δ Q =
Тогда
CP =
é æ |
¶ E |
ö |
|
æ |
¶ V ö |
ù |
|
||||
ê ç |
|
|
÷ |
+ Pç |
|
|
÷ |
ú |
dT |
||
¶ T |
|
|
|||||||||
ë è |
ø P |
|
è |
¶ T ø |
P û |
|
|||||
æ |
¶ E ö |
|
æ |
¶ V ö |
|
|
|||||
ç |
|
|
÷ |
+ |
Pç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|||||
è |
¶ T ø |
P |
è |
¶ T ø P |
|
|
|||||
+éê æç ¶ E ö÷ ë è ¶ P ø T
+ |
æ |
¶ V ö |
ù |
|
Pç |
|
÷ |
ú dP |
|
|
||||
|
è |
¶ P ø |
T û |
|
(3)
Второй член в формуле для CP связан со слагаемым РdV, т.е. описывает эффект, оказываемый на теплоемкость работой, которую система совершает. Для Cv такого слагаемого нет, так как объем постоянный и работа не совершается.
Давайте теперь с помощью якобианов установим связь между этими теплоемкостями: Исходными формулами являются
|
æ |
¶ S ö |
|
æ |
¶ S ö |
||
CV |
= Tç |
|
÷ |
, |
CP = Tç |
|
÷ |
|
|
||||||
|
è |
¶ T ø V |
|
è |
¶ T ø P |
||
|
|
|
æ ¶ S |
ö |
|
= |
|
|
|
¶ (S,V ) |
= |
|
|
|
¶ (S,V ) ¶ (T, P) |
= |
|
¶ (S,V ) æ ¶ V ö − 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
¶ (T,V ) |
¶ |
(T, P) ¶ (T,V ) |
|
¶ (T, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
è ¶ T |
ø |
V |
|
|
|
|
|
|
|
|
P) è |
¶ P ø T |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Распишем якобиан |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
¶ S ö |
|
æ |
|
¶ S |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
¶ (S,V ) |
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
æ ¶ S ö æ |
¶ V ö |
|
|
æ ¶ S ö |
æ ¶ V |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
¶ P |
|
|
|
|
|
|
ö |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|
|
è |
|
¶ T ø P |
|
è |
|
|
ø T |
|
= |
|
|
- |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
¶ V |
ö |
|
|
æ |
¶ V |
|
ö |
|
|
|
ç |
|
|
|
÷ ç |
|
|
÷ |
ç |
|
|
|
|
|
÷ ç |
|
|
÷ |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
¶ (T, P) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è ¶ T ø P è |
¶ P ø |
T |
|
è ¶ P ø T è ¶ T |
ø P |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
ç |
|
¶ P |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
¶ T ø P |
|
è |
|
|
ø T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ V ö − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
||||||||||||||||||||
æ ¶ S ö |
|
|
|
¶ (S,V ) æ |
|
é æ |
|
|
¶ S ö |
æ ¶ V ö |
æ |
|
¶ S ö |
æ |
¶ V ö |
ù |
æ |
¶ V ö |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ç |
|
|
|
÷ |
|
|
= |
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
÷ |
= |
|
ê ç |
|
|
|
÷ |
ç |
|
|
÷ |
|
- ç |
|
|
÷ |
ç |
|
|
÷ |
ú |
ç |
|
÷ |
= |
|||||||||||||||||||
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
¶ P |
|
|
|
|
|
|
¶ T |
|
||||||||||||||||||||||||||||||||||||||||||||||||
è ¶ |
T ø V |
|
|
(T, P) è |
|
ø T |
|
|
|
|
ë è |
|
|
¶ T ø |
P è ¶ |
P ø T |
è |
|
¶ P ø |
T è |
ø |
P û |
è |
¶ P ø |
T |
||||||||||||||||||||||||||||||||||||||||||||
æ |
|
¶ S ö |
|
|
|
|
|
æ |
|
¶ S ö |
æ |
|
¶ V ö |
|
æ ¶ V ö − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= ç |
|
|
÷ |
|
|
|
- |
|
ç |
|
|
|
÷ |
|
ç |
|
|
|
|
|
|
|
÷ |
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
è |
|
¶ T ø |
P |
|
|
|
|
è |
|
¶ P ø T |
è |
T ø P è |
¶ P ø T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Перепишем последнее соотношение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
¶ S ö æ |
|
¶ V ö æ ¶ V |
ö − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
CV = CP - Tç |
|
|
÷ ç |
|
|
|
|
|
|
÷ ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
¶ P ø T |
è |
|
¶ T ø P è ¶ P |
ø T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Учитывая, что от переменных Т и Р зависит потенциал Гиббса
