
Ю.Ф. Глазков Расчет на изгиб со сжатием (растяжением)
.pdfМинистерство образования Российской Федерации
Кузбасский государственный технический университет
Кафедра сопротивления материалов
Расчет на изгиб со сжатием (растяжением)
Методические указания для выполнения расчетно-графического задания
для всех специальностей
Составитель Ю. Ф. Глазков
Утверждены на заседании кафедры Протокол № 1 от 30.08.99
Рекомендованы к печати методической комиссией направления 550100
Протокол № 31 от 09.11.99
Электронная копия находится в библиотеке главного корпуса КузГТУ
Кемерово 2000
1
1.Введение
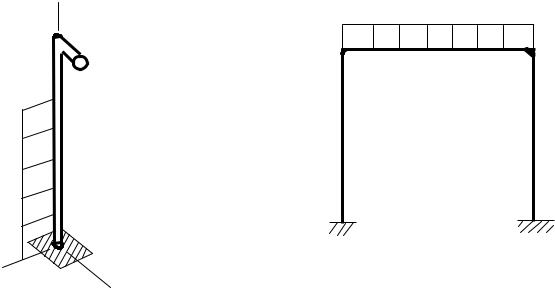
Вслучаях, когда нагрузка на стержневые элементы инженерных конструкций имеет сложный пространственный характер (рис.1,а) или сама конструкция имеет сложный вид (рис.1,б), возникает состояние, которое называется изгибом со сжатием или растяжением (далее – изгиб со сжатием). В этих случаях в поперечных сечениях стержня одно-
временно действуют изгибающие моменты Мx, Мy, поперечные силы Qx, Qy и продольная сила N.
|
z |
q |
|
а) |
|
P |
б) |
|
|||
|
|
|
|
q
Рис.1. Типичные задачи изгиба со сжатием
Изгиб со сжатием является обычным состоянием у многих инженерных конструкций: зданий, сооружений, машин, аппаратов и т.д. Расчеты при изгибе со сжатием имеют ряд отличительных особенностей по сравнению с расчетами других состояний конструкций. Поэтому студенты механических специальностей должны иметь представление об основах таких расчетов.
В задании предполагается выполнение следующих расчетов: 1)определение внутренних усилий от заданной нагрузки; 2)определение нормальных напряжений в целях проверки проч-
ности или подбора сечения (по усмотрению преподавателя) по условию прочности;
3)построение ядра заданного сечения.
2. Основные понятия и сведения из теории
2
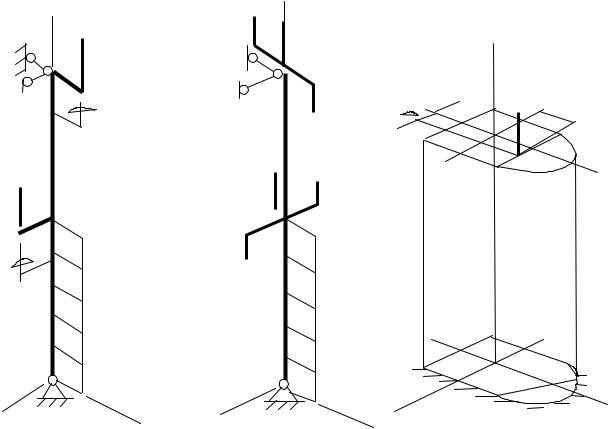
В задании могут быть использованы две основные расчетные схемы стержня, работающего на изгиб со сжатием (рис.2). В первом случае стержень нагружен системой продольных и поперечных нагрузок (рис.2,а), а во втором – одной силой, параллельной оси стержня и имеющей эксцентриситет “e” относительно этой оси (рис.2,в)
z |
|
z |
|
а) |
б) |
в) |
|
Р1 |
|
P1 |
z |
|
|
M1=P1e1 |
P yp |
e1 |
|
xp |
|
Р2 |
M2=P2e2 |
P2 |
|
|
|
|
|
e2 |
|
|
|
q |
|
q |
|
x |
|
x |
y |
y |
x |
y |
|
Рис.2. Расчетные схемы изгиба со сжатием
В первом случае приложенную нагрузку удобно привести к оси стержня с добавлением пар с моментами Мi = Pi ei от внецентренно приложенных сосредоточенных сил Pi (рис.2,в). После этого можно определить внутренние усилия N, Mx, My, Qx, Qy обычными способами, используя правила метода сечений. Если стержень обладает большой жесткостью, то обычно пренебрегают влиянием продольной нагрузки на изгибающие моменты и прогибы. В данных указаниях рассматриваются только такие случаи. Это позволяет определять внутренние усилия, применяя принцип независимости действия сил, когда общая нагрузка разделяется на три независимые группы: продольную и
3
две поперечные, действующие в главных плоскостях стержня. После этих преобразований внутренние усилия находят с помощью приемов, рассмотренных ранее при изучении тем “Растяжение-сжатие” и “Из-
гиб” [4,5].
При оценке прочности в большинстве расчетов учитывают только нормальные напряжения σ , возникающие в поперечном сечении, а касательными напряжениями обычно пренебрегают. Формула для определения нормальных напряжений имеет вид [1,2]
σ = |
|
N |
+ |
My |
x + |
M |
x |
y , |
(2.1) |
|
F |
J y |
|
|
|||||
|
|
|
|
J x |
|
||||
где |
N, Mx, My – продольная сила и изгибающие моменты в расчетном |
||||||||
|
|
|
|
поперечном сечении, н и н м; |
|
||||
|
F, Jx, Jy – |
площадь и моменты инерции поперечного сечения |
|||||||
|
|
|
|
стержня относительно главных центральных осей, м2 и м4; |
|||||
|
|
x, y – координаты расчетной точки сечения относительно глав- |
|||||||
|
|
|
|
ных центральных осей поперечного сечения, м. |
(x,y), ко- |
||||
|
|
Уравнение (2.1) определяет поверхность напряжений σ |
|||||||
торая является плоскостью, не проходящей через начало координат. В практических расчетах бывает полезно найти положение нейтральной оси (н.о.) – прямой, лежащей в плоскости поперечного сечения, на которой выполняется условие
σ |
= |
N |
+ |
My |
x0 + |
M |
x |
y0 = 0, |
(2.2) |
||||||
F |
J y |
|
|
|
|||||||||||
|
|
|
|
|
J x |
|
|
|
|||||||
где x0, y0 – координаты точек сечения, лежащих на н.о., м. |
|
||||||||||||||
|
|
|
Для построения нейтральной оси удобно определять координаты |
||||||||||||
точек ее пересечения с главными осями сечения (рис.3,б) |
|
||||||||||||||
ax |
= − |
|
|
NJ y |
|
; |
ay = |
− |
NJ |
x |
. |
(2.3) |
|||
|
M y F |
|
|
|
|||||||||||
|
|
|
|
|
|
|
M x F |
|
|||||||
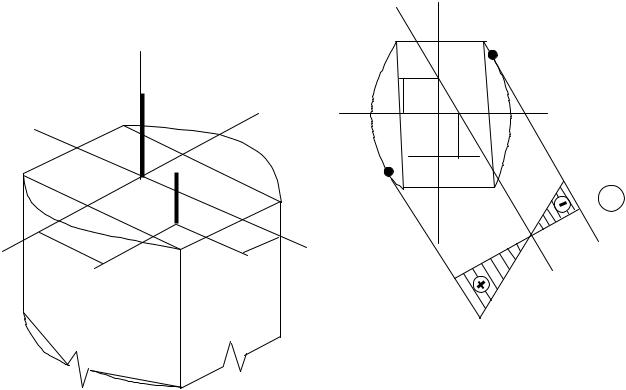
Наибольшие растягивающие и сжимающие нормальные напряжения возникают в точках I и II поперечного сечения (рис.3,б), наиболее удаленных от нейтральной оси.
|
4 |
а) |
б) |
z |
II |
N |
ay |
My  Mx x
Mx x
σ |
I |
ax |
|
|
σ |
y |
|
y |
x
y |
x |
н.о.
Рис.3. Распределение нормальных напряжений в поперечном сечении
Для оценки прочности конструкции обычно используют условия
σ I ≤ [σ ]+ ; σ II ≤ [σ ]− , |
(2.4) |
где σ I, σ II – модули наибольших растягивающих и сжимающих нормальных напряжений в опасном сечении стержня, Па;
[σ ]+, [σ ]- - допускаемые напряжения на растяжение и сжатие для материала заданной конструкции, Па.
Частным случаем изгиба со сжатием является внецентренное сжатие (рис.2,б), когда продольная нагрузка Р действует на стержень с эксцентриситетом “e” относительно его продольной оси.
В этом случае рассмотренные ранее формулы (2.2) и (2.3) принимают следующий вид:
|
|
P |
|
|
|
xpx |
|
ypy |
|
||||
σ |
= − |
|
|
(1+ |
|
|
|
+ |
|
|
); |
(2.5) |
|
F |
|
i2 |
i2 |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
|
x |
|
|
||
a |
|
iy2 |
|
|
a = − |
i2 |
|
|
|||||
= − |
|
|
|
; |
x |
, |
|
(2.6) |
|||||
|
|
|
|
|
|||||||||
x |
|
xp |
|
y |
|
yp |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
5
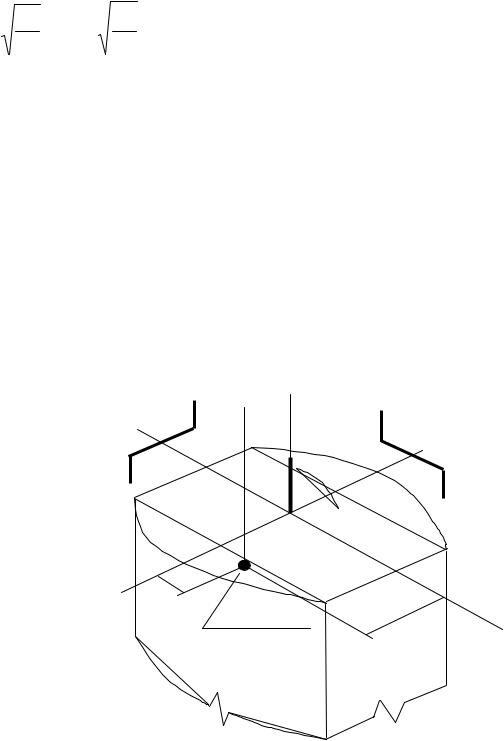
где xP, yP – координаты “полюса” (рис.4,б) – следа линии действия нагрузки Р в плоскости расчетного поперечного сечения стержня, м;
ix, iy – радиусы инерции расчетного поперечного сечения стержня относительно его главных центральных осей, м.
Радиусы инерции определяются по формулам
ix = |
J |
x |
; iy = |
J y |
. |
(2.7) |
|
F |
|||||
|
F |
|
|
|
||
В нормах проектирования некоторых инженерных конструкций считается, что изгиб со сжатием эквивалентен состоянию внецентренного сжатия силой N, приложенной с эксцентриситетами относительно главных осей сечения xP = My / N, yP = Mx / N.
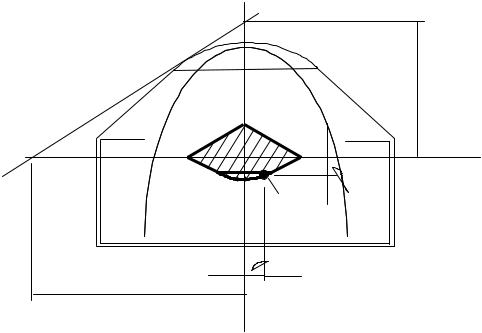
При расчетах внецентренно сжатых конструкций, материал которых по разным причинам плохо сопротивляется растяжению, бывает полезно ограничивать положение полюса p(xP, yP) некоторой областью, расположенной вокруг центра тяжести поперечного сечения и обладающую тем свойством, что при нахождении полюса внутри ее эпюра напряжений σ во всем сечении имеет один знак. Эта область называется ядром сечения и является его специальной геометрической характеристикой.
P
My= - P xp |
Mx= - P xp |
N= - P
x
yp
полюc ”p” |
xp |
y |
Рис.4. Нагрузка и внутренние усилия при внецентренном сжатии
6
Контур ядра сечения можно определить как геометрическое место полюсов, соответствующих множеству нейтральных осей, касательных с контуру сечения (рис.5). Для конкретной нейтральной оси i после замера координат ax и ay положение соответствующего ей полюса можно определить по формулам
xp |
= − |
iy2 |
; |
yp |
= − |
i |
2 |
. |
(2.8) |
|
|
x |
|||||||
ax |
|
|
|||||||
|
|
|
|
|
ay |
|
|||
При построении ядра сечения полезно учитывать следующие правила:
1) ядро сечения строится только для выпуклой части контура сечения (пунктирная линия на рис.5);
2)вершине на контуре сечения соответствует прямая линия на контуре ядра сечения;
3)прямой линии на контуре сечения соответствует вершина на контуре ядра сечения;
4)кривой на контуре сечения соответствует кривая на контуре ядра сечения.
y
ayi
н.о. i |
x |
pi ypi
axi |
xpi |
Рис.5. К построению ядра сечения
3. Пример расчета
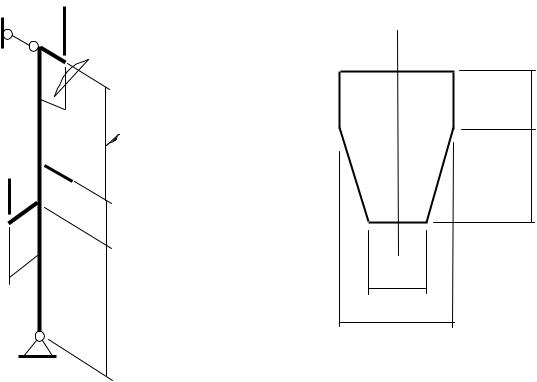
Для стойки (рис.6,а) необходимо найти внутренние усилия от заданной нагрузки и подобрать сечение заданной формы (рис.6,б) по условию прочности. Материал конструкции – серый чугун марки
7
СЧ 12 – 28. Коэффициент запаса прочности принять равным n = nв = 3,0. Построить ядро подобранного сечения и построить эпюру нормальных напряжений в одном из сечений стержня.
3.1.Определение внутренних усилий
После переноса продольных нагрузок Р1 и Р2 на ось стойки к изгибающей нагрузке добавляются две пары сил с моментами М1 =
=Р1e1 = 30 0,02 = 0,6 кН м и М2 = Р2e2 = 50 0,04 = 2,0 кН м.
Вдальнейшем нагрузка разбита на три группы: продольную и
две изгибающие. Эти нагрузки показаны на рис.7.
а) |
Р1=30 кН |
б) |
e1=0,02 м |
|
0,5 м |
a |
|
|
P2=50 кН |
|
Р3=2 кН |
2a |
0,2 м |
|
e2=0,04 м |
a |
|
|
0,6 м |
2a |
Рис.6. Схемы нагрузок (а) и поперечного сечения (б) к примеру расчета
а. Определение продольных сил N
Уравнение равновесия:
Σ z = 0; HA –P2 – P1 =0;
HA = P1 + P2 = 80 кН.
8
а) |
|
|
|
|
Ha=80 кН |
Р2 |
|
Р1 |
|
A |
C |
D |
B |
|
0,6 м |
0,2 м |
0,5 м |
|
|
N |
|
|
30 |
|
|
|
|
||
80 |
|
|
|
|
Vay=0,308кН |
P3 |
Vby = 1,69кН |
|
|
б) |
|
M1=0,6 кН м |
z |
|
y |
|
|||
|
0,308 |
|
||
Qy |
|
|
|
|
|
1,69 |
|
0,6 |
|
|
|
|
||
Mx |
|
|
|
|
0,19 |
0,25 |
|
||
Vax=1,54 кН |
|
Vbx=Vax |
|
|
в) |
M2=2,0 кН м |
z |
||
x |
||||
|
|
|
||
Qx
1,54
0,95
My
1,05 0,77
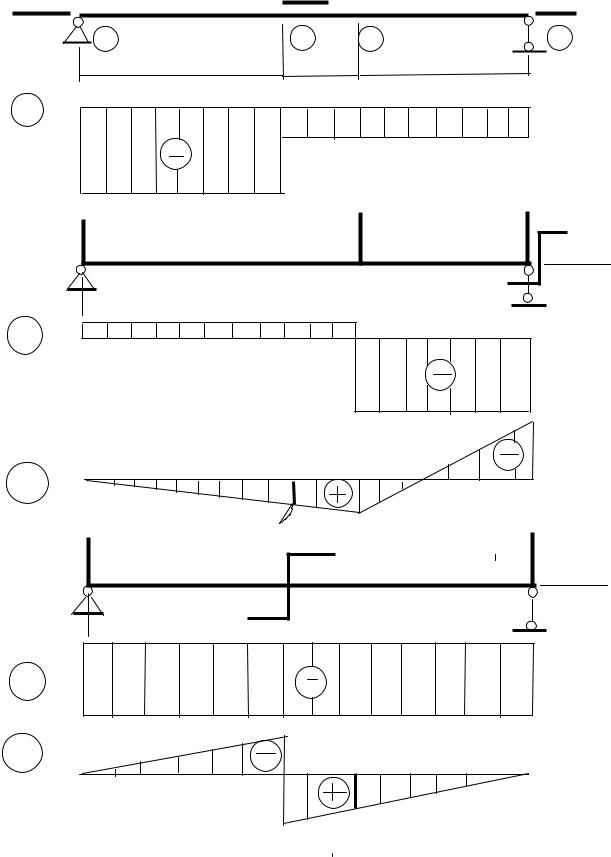
Рис.7. Схемы нагрузок и эпюры внутренних усилий

9
Продольные силы по участкам:
N1 = -HA = -80 кН; N2 = -P1 = -30 кН.
б. Определение внутренних усилий Мх и Qy
Уравнения равновесия:
Σ mB = 0; -VAY 1,3 + P3 0,5 – M1 = 0; VAY = (2,0 0,5 – 0,6) / 1,3 = 0,308 кН.
Σ mA = 0; VBY 1,3 – P3 0,8 – M1 = 0;
VBY = (2,0 0,8 – 0,6) / 1,3 = 1,69 кН.
Поперечные силы QY по участкам:
Q1Y = VAY = 0,308 кН; Q2Y = - VBY = -1,69 кН.
Изгибающие моменты MX в характерных сечениях:
MCX = VAY 0,6 = 0,308 0,6 = 0,19 кН м; MDX = VAY 0,8 = 0,308 0,8 = 0,25 кН м; MBX = - M1 = - 0,6 кН м.
Эпюры QY и MX показаны на рис.7,б.
в. Определение внутренних усилий QX и MY
Уравнения равновесия:
Σ mB = 0; VAX 1,3 – M2 = 0; VAX = VBX = M2 / 1,3 = 1,54 кН.
Поперечные силы QX по участкам:
Q1X = Q2X = - VAX = - 1,54 кН.
Изгибающие моменты MY в характерных сечениях:
MCYлев = - VAX 0,6 = - 1,54 0,6 = - 0,93 кН м; MCYправ = VBX 0,7 = 1,54 0,7 = 1,07 кН м; MDY = VBX 0,5 = 1,54 0,5 = 0,77 кН м.
