
- •1) Определение должно быть соразмерным.
- •2) Определение должно быть четким и ясным.
- •4) Определение по возможности не должно быть отрицательным.
- •§ 2. Виды аналогии
- •§ 2. Состав аргументации: субъекты, структура Субъекты аргументации
- •3. Демонстрация — это логическая связь между аргументами и тезисом.
- •2. Косвенным называют обоснования тезиса путем установления ложности антитезиса или других конкурирующих с тезисом допущений.
- •30. Обоснование тезиса
- •1. Прямым называют обоснование тезиса без обращения к конкуриру
предмет логики- законы и формы приема и операции мышления с помощью которых человек познает мир
Значение логики
Наше мышление подчиняется логическим законам и протекает в логических формах независимо от науки логики. Люди мыслят логично, даже не зная, что их мышление подчиняется логическим закономерностям. Но следует ли из этого, что изучение логики излишне? Знание законов и форм мышления, их сознательное использование в процессе познания повышает культуру мышления, вырабатывает навык мыслить более «грамотно», развивает критическое отношение к своим и чужим мыслям. Поэтому взгляд, будто изучение логики не имеет практического значения, несостоятелен.
Сторонники такого взгляда ссылаются иногда на ироническое замечание Гегеля о том, что логика учит мыслить так же, как физиология «учит» переваривать. Разумеется, можно правильно мыслить, не изучив логику, а переваривать пищу, не зная физиологии пищеварения. Однако нельзя и недооценивать практического значения этих наук. Когда академика И.П. Павлова спросили, в чем он видит основные цели физиологической науки, великий русский физиолог ответил: «Задачей физиологии является научить человека, как правильно есть, дышать, как правильно работать и отдыхать, чтобы прожить как можно дольше».
Что касается логики, то ее задача состоит в том, чтобы научить человека сознательно применять законы и формы мышления и на этой основе логичнее мыслить и, следовательно, правильнее познавать окружающий мир.
Основоположники марксизма, мастерски владея диалектической логикой, отмечали важную роль формальнологической правильности мышления, вскрывали логические ошибки и уловки в рассуждениях идейных противников. Известны слова В.И. Ленина о том, что от марксиста «можно требовать больше логики», чем от немарксиста.
Мыслить логично — это значит мыслить точно и последовательно, не допускать противоречий в своих рассуждениях, уметь вскрывать логические ошибки. Эти качества мышления имеют большое значение в любой области научной и практической деятельности, в том числе и в работе юриста, требующей точности мышления, обоснованности выводов.
Лучшие русские юристы отличались не только глубоким знанием всех обстоятельств дела и яркостью судебных речей, но и строгой логичностью в изложении и анализе материала, неопровержимой аргументацией выводов. Вот, например, как характеризуется профессиональное мастерство известного русского адвоката второй половины прошлого века П.А. Александрова: «Наиболее характерным для судебного ораторского мастерства П.А. Александрова является твердая логика и последовательность его суждений, умение тщательно взвешивать и определять место любого доказательства по делу, а также убедительно аргументировать и обосновывать свои важнейшие доводы». А.Ф. Кони подчеркивал «неотразимую логику» в речах В.Д. Спасовича. Строгая последовательность, логичность и убедительность отмечаются в речах видного юриста К.Ф. Халтулари.
И наоборот, рассуждения, в которых отсутствует строгая логика, непоследовательные и противоречивые, затрудняют выяснение дела, а в некоторых случаях могут явиться причиной вынесения неправильного приговора. Знание логики помогает юристу подготовить логически стройную, хорошо аргументированную речь, вскрыть противоречия в показаниях потерпевшего, свидетелей, обвиняемого, опровергнуть необоснованные доводы своих оппонентов, построить судебную версию, наметить логически выдержанный план осмотра места происшествия, непротиворечиво, последовательно и обоснованно составить официальный документ и т. д. Все это имеет важное значение в работе советского юриста, направленной на укрепление социалистической законности и правопорядка.
2. С развитием трудовой материально-производственной деятельности людей совершенствовались их мыслительные способности, а это привело к тому, что объектом исследования становится само мышление, его формы и законы.
Отдельные логические проблемы возникли в I тыс. до н. э. сначала в Древней Индии и Китае, а затем в Древней Греции и Риме. Постепенно они оформляются в стройную систему знаний, в самостоятельную науку.
Основными причинами возникновения логики являются развитие наук и ораторского искусства. Наука основывается на теоретическом мышлении, предполагающем умозаключения и доказательства. Отсюда необходимость исследования самого мышления как формы познания. Ораторское искусство проявлялось прежде всего в многочисленных судебных заседаниях как потрясающая умы сила убеждения, буквально заставляющая слушателей склониться к тому или другому мнению. Логика возникает как попытка раскрыть тайну этой принудительной силы речей.
В Древней Греции логику разрабатывали Парменид, Зенон, Демокрит, Сократ, Платон. Однако основателем науки логики считается величайший мыслитель древности, ученик Платона – Аристотель (384–322 до н. э.). Он называл свое творение аналитикой, термин «логика» вошел в научный оборот позднее, в III в. до н. э.
После Аристотеля в Древней Греции логика разрабатывалась стоиками. Древнеримские политические деятели Цицерон и Квинтилиан, арабоязычные ученые – Аль Фараби, Ибн Рушд, европейские средневековые схоласты – У Оккам, П. Абеляр.
В эпоху Нового времени философ Ф. Бекон (15611626) опубликовал свое исследование под названием «Новый Органон», в нем содержались основы индуктивных методов, усовершенствованные позже Д.С. Миллем (1808–1873) и получившие название методов установления причинных связей между явлениями (методы Бекона – Милля).
В 1662 г. был издан учебник «Логика Пор-Рояля». Его авторы П. Николь и А. Арно создали логическое учение, основанное на методологических принципах Р. Декарта (1596–1650).
Логика, созданная на основе учения Аристотеля, существовала до начала ХХ в. В ХХ в. активно развивается символическая (математическая) логика, основанная на идее немецкого ученого и философа Лейбница (1646–1716), о возможности сведения рассуждений к вычислениям. Такая логика начала формироваться в середине Х1Х в. Ее развитие связано с именами Дж. Буля, А.М. Де-Моргана, Ч. Пирса, Г. Фреге, русских мыслителей П.С. Порецкого и Е.Л. Буницкого и др. Первым капитальным трудом по символической логике была работа Б. Рассела и А. Уайтхеда «Principia Mathematika» в 3-х т., вышедшая в 19101913 гг. Эта работа вызвала революцию в логике.
Идеи диалектической логики восходят к античной и древневосточной философии, но законченную форму им придали только представители немецкой классической философии: Кант (1724–1804), Фихте (1762–1814), Шеллинг (1775–1854) и особенно Гегель (1770–1831), окончательно сформулировавший основные идеи диалектики с точки зрения объективного идеализма.
Диалектическую логику на материалистической основе разрабатывали К. Маркс, Ф. Энгельс, В. Ленин.
3 .Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание и умозаключение.
Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя». Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров. Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно. По форме высказывание является повествовательным предложением.Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка их истинности или ложности невозможна. Высказывания могут быть выражены с помощью не только естественных языков, но и формальных. Например, высказывание на естественном языке имеет вид «Два умножить на два равно четырем», а на формальном, математическом языке оно записывается в виде: «2 • 2 = 4». Истинность высказываний может зависеть от взглядов людей, от конкретных обстоятельств и так далее. Сегодня высказывание «На моем компьютере установлен самый современный процессор Pentium 4» ложно, но некоторое время назад оно было истинным. Высказывания бывают общими, частными или единичными. Общее высказывание чаще всего начинается со слов: все, всякий, каждый, ни один. Частное высказывание можно начать со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным. На основании простых высказываний могут быть построены составные высказывания. Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединенных союзом «и». Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла, то истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний. Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение). Например, если мы имеем суждение «Все углы треугольника равны», то мы можем путем умозаключения доказать, что в этом случае справедливо суждение «Этот треугольник равносторонний».
Закон тождества
Всякая мысль в процессе рассуждения должна быть тождественна самой себе.
А есть А
Закон непротиворечия
Два несовместимые друг с другом суждения не могут быть одновременно истинными по крайней мере одно из них необходимо ложное.
Неверно что А и не А
Закон исключенного третьего
Два противоречащих суждения не могут быть одновременно ложнами, одно из них необходимо истинно
А есть либо В, либо не В
4. Язык - знаковая информационная система выполняющая функцию хранения формирования и передачи информации в процессе познания действительности и общения между людьми.
Основным строительным материалом при конструировании языка выступают используемые в нем знаки. Знак – это любой чувственно воспринимаемый (зрительно, на слух или иным способом) предмет, выступающий представителем другого предмета. Среди различных знаков выделим два вида: знаки-образы и знаки-символы.
язык логики высказываний. Он применяется в логической системе, называемой исчислением высказываний, которая анализирует рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений. Принципы построения этого языка будут изложены в главе о дедуктивных умозаключениях.
Второй язык – это язык логики предикатов. Он применяется в логической системе, называемой исчислением предикатов, которая при анализе рассуждений учитывает не только истинностные характеристики логических связок, но и внутреннюю структуру суждений.
Имя – это имеющее определенный смысл языковое выражение в виде отдельного слова иди словосочетания, обозначающее или именующее какой-либо внеязыковой объект.
Предметное значение (денотат) имени – это один или множество каких-либо объектов, которые этим именем обозначаются.
Смысловое значение (смысл, или концепт) имени – это информация о предметах, т.е. присущие им свойства, с помощью которых выделяют множество предметов.
Имя – смысл – денотат
Это значит, что имя денотирует, т.е. обозначает объекты только через смысл, а не непосредственно.
Имена признаков – качеств, свойств или отношений – называются предикаторами. В предложении они обычно выполняют роль сказуемого (например, «быть синим», «бегать», «дарить», «любить» и т.д.). Число имен предметов, к которым относится предикатор, называется его местностью. Предикаторы, выражающие свойства, присущие отдельным предметам, называются одноместными (например, «небо синее»). Предикаторы, выражающие отношения между двумя и более предметами, называются многоместными. Например, предикатор «любить» относится к двухместным («Мария любит Петра»), а предикатор «дарить» – к трехместным («Отец дарит книгу сыну»).
Алфавит языка логики предикатов включает следующие виды знаков (символов):
1) а, Ь, с,... – символы для единичных (собственных или описательных) имен предметов; их называют предметными постоянными, пли константами;
2) х, у, z, ... – символы общих имен предметов, принимающие значения в той или другой области; их называют предметными переменными;
3) Р', О', R',... – символы для предикатов, индексы над которыми выражают их местность; их называют предикатными переменными;
4) р, q, г, ... – символы для высказываний, которые называют высказывательными, или пропозициональными переменными (от латинского propositio – «высказывание»);
5) V, 3 – символы для количественной характеристики высказываний; их называют кванторами: V – квантор общности; он символизирует выражения – все, каждый, всякий, всегда и т.п.; 3 – квантор существования; он символизирует выражения – некоторый, иногда, бывает, встречается, существует и т.п.;
6) логические связки:
Л –– КОНЪЮНКЦИЯ (СОЮЗ «И»);
V –– ДИЗЪЮНКЦИЯ (СОЮЗ «ИЛИ»);
–> – импликация (союз «если..., то...»);
= – эквиваленция, или двойная импликация (союз «если и только если..., то...»); .
Ч – отрицание («неверно, что...»). Технические знаки языка: (, ) – левая и правая скобки.
5. Понятие – это форма мышления, отражающая предметы в их существенных признаках. Признаком предмета называется то, в чем предметы сходны друг с другом или чем они друг от друга отличаются. Любые свойства, черты, состояние предмета, которые, так или иначе, характеризуют предмет, выделяют его, помогают распознать среди других предметов, составляют его признаки. Признаками могут быть не только свойства, принадлежащие предмету; отсутствующее свойство (черта, состояние) также рассматривается как его признак. Любой предмет имеет множество разнообразных признаков. Одни из них характеризуют отдельный предмет и являются единичными, другие принадлежат определенной группе предметов и являются общими. Так, каждый человек имеет признаки, одни из которых, например, черты лица, телосложение, походка, мимика, так называемые особые приметы, броские признаки, принадлежат только данному человеку и отличают его от других людей. Другие профессия, национальность, социальная принадлежность и т. д. являются общими для определенной группы людей. И, наконец, есть признаки, общие для всех людей. Они присущи каждому человеку и вместе с тем отличают его от всех других живых существ. К ним относятся способность создавать орудия труда, способность к абстрактному мышлению и членораздельной речи. Кроме единичных (индивидуальных) и общих признаков логика выделяет признаки существенные и несущественные. Признаки, необходимо принадлежащие предмету, выражающие его сущность, называют существенными. Они могут быть общими и единичными. Понятия, отражающие множество предметов, включают общие существенные признаки (напр. способность создавать орудие труда). Понятие, отражающее один предмет (напр. “Аристотель”), наряду с общими существенными признаками (человек, древнегреческий философ) включает единичные признаки. Признаки, которые могут принадлежать, но могут и не принадлежать предмету и которые не выражают его сущность, называются несущественными. Понятие качественно отличается от форм чувственного познания: ощущений, восприятия и представлений, существующих в сознание человека в виде наглядных образов отдельных предметов или их свойств. Восприятие и представление – это чувственно-наглядный образ какого-либо конкретного предмета. Понятие лишено наглядности. Понятие как форма мышления отражает предметы и их совокупность в абстрактной, обобщенной форме на основании их существенных признаков. Понятие – одна из основных форм научного познания. Формируя понятие, наука отражает в них изучаемые ею предметы, явления, процессы. Отражая существенное, понятия не содержат всего богатства индивидуальных признаков предмета и в этом смысле они беднее форм чувственного познания – восприятия и представления. Вместе с тем, они позволяют глубже проникнуть в действительность, отобразить её с большей полнотой, на что не способно чувственное познание.( также см вопрос № 3 ).
Понятие неразрывно связано с основной языковой единицей – словом. Понятие выражается и закрепляется в словах и словосочетаниях, без которых невозможно ни формирование понятий, ни оперирование имени (это слова и словосочетания, имеющие определённый смысл и обозначающие какой-либо предмет). Омонимы – это слова, совпадающие по звучанию, одинаковые по форме, но выражающие различные понятия. Синонимы – это слова, близкие или тождественные по своему значению, выражающие одно и тоже понятие, но отличающиеся друг от друга оттенками значения или стилистической окраской. Многозначность слов нередко приводит к смешению понятий, а, следовательно, к ошибкам в рассуждениях. Поэтому необходимо точно установить значение слов, с тем, чтобы употреблять их в строго определённом смысле. Термин - это слово или словосочетание, обозначающее строго определенное понятие и характеризующееся однозначностью, по крайней мере, в пределах данной науки или родственной группы наук.
6. Основными логическими приемами формирования понятий являются анализ, синтез, сравнение, абстрагирование, обобщение. Понятие формируется на основе обобщения существенных признаков (т.е. свойств и отношений), присущих ряду однородных предметов. Анализ – мысленное расчленение предметов на их составные части, мысленное выделение в них признаков. Синтез мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа. Сравнение – мысленное установление сходства или различия предметов по существенным или несущественным признакам. Абстрагирование – мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделении существенных признаков предметов и в отвлечении от несущественных , второстепенных. Обобщение – мысленное объединение отдельных предметов в некотором понятии. Итак, перечисленные выше логические приемы используются на уроках в школе при формировании новых понятий.
7. Содержание понятия составляют все его элементы, которые могут быть выделены в качестве отдельных понятий. Объем понятия есть все другие понятия, для которых оно служит признаком, главной их частью.
Закон обратного отношения между объемом и содержанием понятий имеет силу только для тех понятий, одно из которых является родовым (подчиняющим), а другое видовым (подчиненным).
Если первое понятие шире второго по объёму, то оно беднее его по содержанию; если же первое понятие у́же второго по объему, то оно богаче его по содержанию. Например, понятие «физика» обладает ме́ньшим объёмом, чем понятие «наука». При этом содержание понятия «физика» больше (богаче), чем содержание понятия «наука», так как помимо своих собственных содержит все признаки понятия «наука».
Закон применим только при вхождении объёма одного понятия в объём другого, например: «животное» — «собака». Закон не работает для несовпадающих понятий, например: «книга» — «кукла».
Уменьшение объёма понятия с добавлением новых признаков наступает не всегда, а только когда признак свойственен части объёма исходного понятия
8. 1. Основанием для этого деления является наличие или отсутствие в содержании понятия признаков, отвечающих на вопросы «где?», «когда?», «какого рода индивидуум?». Если эти признаки есть, понятия называются регистрирующими, если нет – нерегистрирующими.
Примеры регистрирующих понятий: «народы Европы», «средневековая философия»
Примеры нерегистрирующих понятий: «человек», «деревья», «камни», «планеты»
Регистрирующие понятия по объему, т.е. по количеству мыслимых посредством них индивидуумов, делятся на общие (множественные) и единичные. Примеры общих (множественных) понятий: «жители Харькова», «выдающиеся деятели культуры», «студенты ХНУРЭ», «молодые специалисты» и т.п. Примеры единичных понятий: «Альберт Эйнштейн», «президент академии наук», «чемпион мира по плаванию»
Пустыми называются понятия, которым не соответствует ни один предмет в объективном мире. Например, «вечный двигатель», «эфир» (не легкая жидкость, а материальная субстанция), «кентавр», «звездолет», «терминатор» и т.п. Соответственно, непустымиявляются понятия, соответствующие каким-либо предметам действительности; например: «Млечный путь», «страны СНГ», «теория относительности», «кафедра философии»
Конкретными являются понятия о предметах, а абстрактными – о свойствах и отношениях. Например, конкретными являются понятия: «машина», «дом», «дорога», «деньги» и т.п.; абстрактными понятиями являются: «стойкость», «красота», «надежность», «сила», «координация», «субординация»
Относительные понятия имеют в своем содержании признак, фиксирующий отношение одного предмета к другому, например, «отец», «друг», «учитель», «сосед», «начальник» и т.п. В содержании абсолютного понятия (безотносительного понятия) такой признак отсутствует; например: «корпус», «искусство», «наука», «политика», «учеба» и т.п. Следует различать относительные понятия и понятия об отношениях, такие, как «южнее», «выше», «больше», «сильнее»
положительные и отрицвтельные.
Отрицательные понятия фиксируют те признаки (признак), которые отсутствуют в предмете, т.е. здесь имеет место обобщение по отсутствию признаков. Но понятие, в котором мыслится лишь отсутствие признаков предмета, невозможно. Приведем пример таких понятий: «не-человек», «не-млекопитающее», «не-наука» Таким образом, в отрицательных понятиях мыслится не отрицание признаков соотносительного положительного понятия, а только отличие видового признака первого от видового признака второго при наличии одного и того же родового признака у обоих понятий. Положительные понятия с учетом этого принято обозначать символом Аавс, а отрицательные – символом Авсх, где верхняя черта означает отрицание видового отличия авс, а х – неопределенное видовое отличие.
9. Основными логическими операциями с понятиями являются: обобщение и ограничение понятий, их определение и деление. В основе данных операций лежат родо-видовые отношения между понятиями. Логические операции обобщения и ограничения основаны на законе обратного отношения между объемом и содержанием понятия. Данные операции имеют противоположную направленность. Ограничением называется логическая операция перехода от родовых понятий к видовым путем прибавления к содержанию родового понятия видообразующего признака. Например, если к содержанию понятия «юрист» добавить видообразующий признак, показывающий его специализацию, то получим новое понятие «юрист-криминолог», которое является видовым понятием по отношению к исходному, родовому понятию. Логическая операция ограничения понятия широко применяется в правовой деятельности, в частности при квалификации конкретного преступления. В этом случае осуществляется последовательный переход от понятия с большим объемом к понятию с меньшим объемом. Например, «деяние» —-> «административное нарушение» ——> «уголовное преступление» —-> «разбой». При ограничении понятий важно соблюдать правило последовательного перехода от рода к виду. Пределом ограничения является единичное понятие, например, «юрист-криминолог Артемьев Петр Аркадьевич, 1964 года рождения, проживающий в городе Москве на улице Тверской в доме № 151», потому что объем такого понятия уменьшить уже невозможно: в нем мыслится только один конкретный человек. Обобщением называется логическая операция перехода от видового понятия к родовому путем исключения из содержания данного видового понятия его видообразующего признака. Так, если из содержания понятия «юридическая академия» исключить видовой признак «юридическая», то получим родовое понятия «академия». Для соблюдения правильности обобщения необходимо последовательно переходить от вида к роду, включающему в себя данный вид. Пределом обобщения являются категории. Категории - это наиболее общие фундаментальные понятия, отражающие существенные, закономерные связи объективной действительности и познания. Категории наук различаются по степени общности. Самыми общими являются философские категории. Таким образом, изменяя объем исходного понятия, мы изменяем и его содержание, осуществляя тем самым переход к новому понятию - с большим объемом и меньшим содержанием (обобщение) или с меньшим объемом и большим содержанием (ограничение). Логические операции обобщения и ограничения имеют большое значение в процессе мышления: переходя от понятий одного объема к понятиям другого объема, мы уточняем предмет нашей мысли, делаем наше мышление более определенным и последовательным.
10. Часто возникает необходимость раскрыть содержание понятия, которое употребляется в рассуждении. Так, чтобы правильно изучать
логику нужно знать содержание понятия " Понятие " (Понятие - форма мышления, отражающая предметы в их общих существенных признаках).
Логическая операция, раскрывающая содержание понятия путем перечисления входящих в него признаков называется определением понятия или дефиницией. Как известно содержание понятия - это совокупность существенных признаков предмета
Как дать определение (построить дефиницию)? Определение состоит в их последовательном перечислении.
Указание главной части содержания понятия имеет вид подведения определяемого под ближайшее родовое понятие. Указание побочной части фиксирует те особенные (видообразующие) признаки, которые отличают определяемое от всех, с которыми оно соподчинено родовому понятию. Поэтому стандартная процедура определения называется определением через ближайший род и видообразующие признаки. Такое построение дефиниции не является единственно возможным, но оно встречается чаще всего. Также используется генетическое определение понятия.
Построение дефиниции должно подчиняться ряду правил.
1) Определение должно быть соразмерным.
Иначе говоря, следует перечислять только общие существенные признаки предметов, мыслимых в определяемом. В противном случае определение будет несоразмерным, что является логической ошибкой.
2) Определение должно быть четким и ясным.
В определениях не должно содержаться метафор, сравнений, неизвестных понятий. Все это чревато непониманием или нарушением закона тождества, поэтому в научно-философском, юридическом языке или в деловом общении недопустимо. Например, "Логика это круто" или "Преподаватель - кладезь знаний".
Приведенные суждения будят воображение, они уместны в художественной литературе, но в качестве строгих дефиниций недопустимы.
В определении не должно содержаться круга.
Это правило является частным случаем предыдущего: оно предостерегает против определение неизвестного понятия через однородное ему или производное от него, которое, естественно, тоже не может считаться известным. Пример "Логика—закон о логических принципах".
Но тот, кто не знает значения понятия “ Логика ”, вряд ли знаком с определением “логических”. Поэтому правильная дефиниция должна раскрывать содержание искомого понятия, данное в независимых от определяемого сравнительно простых терминах.
4) Определение по возможности не должно быть отрицательным.
То есть в определении понятия следует фиксировать наличие существенных признаков мыслимых в нем предметов, а не их отсутствие. В противном случае определение неинформативно. Например, суждение: “Реферат – не диссертация” хотя и справедливо, однако практически ничего не говорит о реальном реферате.
Однако в некоторых случаях существенной может быть фиксация именно отсутствия признака, например: ”Отчисленный - человек, не сдавший академическую задолженность”.
Существуют операции, заменяющие определение (описание и характеристика)
Описание состоит в том, чтобы полно и точно указать адресату интересующие его признаки предмета, создать его наглядный образ.
Описание выходит за круг чисто логических операций, оно апеллирует скорее к чувственному восприятию конкретного предмета. Описание не объективно, оно имеет субъективную направленность, то есть строится с учетом того, что нужно конкретному потребителю информации (тогда как определение стремится к объективности, независимости от учета интересов того или иного субъекта).
Характеристика - операция, заменяющая определение тогда, когда оно невозможно или не требуется. Характеристика состоит в том, что перечисляются отличительные признаки или параметры предмета, имеющие значение для адресата. Характеристика, в отличие от описания, не направлена на создание наглядного образа мыслимого предмета. Она может быть использована тогда, когда этот образ вообще не существует.
Логическая операция, раскрывающая объем родового понятия путем перечисления соответствующих ему видовых понятий называется Делением. Термин "деление понятия" описывает два взаимосвязанных процесса: мысленное деление объема родового понятия на подклассы, а также соотнесение родового и вводимых для описания образовавшихся подклассов видовых понятий.
Логическая операция, состоящая в ряде последовательных актов деления, называется классификацией. Деление и классификация - по сути однородные операции, различающиеся лишь количественно (числом актов деления). Но если в случае деления понятия акцент обычно делается на одном из параллельных процессов - на установлении соотношения "родовое понятие - видовые понятия", то в случае классификации - на втором, а именно на подразделении исходного класса на все более мелкие подклассы (объемы видов и “видов видов”...). Поэтому обычно говорят "деление понятия", но “классификация предметов” (например, бабочек или законов).
В структуре логического деления есть три элемента: делимое (родовое понятие), члены деления (видовые понятия), основание деления. Основание деления - признак (или совокупность признаков), по которому проводится деление. В зависимости от характера основания логическое деление делится на виды: дихотомическое и деление по видоизменению признака.
Деление понятия (классификация) должно подчиняться ряду правил. 1) Деление должно быть соразмерным. Иначе говоря, объединение объемов членов деления должно давать объем делимого понятия. Нарушение данного правила - несоразмерное деление (некоторые члены не указываются). Если нет возможности или необходимости перечислять все члены деления, то процедура корректно "закрывается" выражениями типа “и так далее”, “и тому подобное” и им подобным, а также троеточием. 2) Деление должно проводиться по одному основанию. Нарушение этого правила будет состоять в том, что процесс деления ведут по одному основанию, а продолжают,/заканчивают по другому, Например: студенты делятся по успеваемости на успевающих и неуспевающих. По национальному признаку - русские, евреи, узбеки. Но нельзя смешивать и делить на успевающих, неуспевающих и узбеков (хотя связь может быть) 3) Члены деления должны исключать друг друга. Иначе говоря, в результате деления должно получить несовместимые (точнее, соподчиненные) понятия. Причиной нарушения этого правила бывает нарушение предыдущего. 4) В ходе классификации деление должно быть непрерывным. Это значит, что в процессе деления исходного родового понятия следует переходить к его ближайшим видовым, не пропуская (“не перескакивая”) их. В противном случае возникает ошибка - “скачок в делении”. Типичный ее пример: "Живые существа делятся на растения, млекопитающих животных и студентов заочников "
Виды деления. В настоящее время принято выделять два основных вида деления: таксономическое и мереологическое.
Таксономическое деление. Если с помощью определения раскрывается содержание понятия, то с помощью таксономического деления – его объем. Таксономическое деление – это операция разбиения объема родового понятия на подклассы, представляющие собой виды предметов, мыслимых в понятии (таксоны). Таксономическое деление, в свою очередь, бывает двух видов:
а) по видообразующему признаку (основанию).
Пример. Механическое движение (рассматриваемое в некотором отрезке времени) можно разделить по характеру траектории (основание деления) на прямолинейное, криволинейное, колебательное. В зависимости от состояния скорости во времени (другое основание деления) можно выделить равномерное, равноускоренное и равнозамедленное движение;
б) дихотомическое – деление исходного объема на объемы противоречащих друг другу понятий.
Пример 1. Грибы можно разделить на съедобные и несъедобные.
При этом для таксономического деления оказывается справедливой следующая характеристика родо-видовых отношений: то, что можно сказать о роде, можно сказать и о виде.
Пример 2. Прямолинейное, криволинейное, колебательное движения обладают всеми признаками движения вообще, съедобные грибы – всеми признаками грибов вообще.
Мереологическое деление. В отличие от таксономического деления, в процессе которого выявляются виды предметов некоторого рода, мереологическое деление есть расчленение некоторого предмета на части.
Пример 1. Самолет состоит из частей: крыльев, фюзеляжа, мотора, управляющей системы, шасси. При этом каждую из частей, в свою очередь, можно подразделить на части.
Отношение целого и части характеризуется следующим: то, что можно сказать о целом, нельзя сказать о части.
Пример 2. Крылья, фюзеляж, мотор – это еще не самолет.
12. Операции с классами — это такие логические действия, которые приводят нас к образованию нового (в общем случае) класса.
Существуют следующие операции с классами: объединение, пересечение, вычитание, дополнение.
Объединение («сложение») классов
Объединение (или сумма) двух классов — это класс тех элементов, которые принадлежат хотя бы к одному из этих двух классов17: Объединение обозначается: или Объединение класса четных чисел с классом нечетных чисел дает класс целых чисел. Объединив класс поэтов и класс советских поэтов, получим класс поэтов.
При выражении операции объединения классов пользуются обычно союзом «или» в не исключающем смысле. Например, говоря, что некто — член волейбольной или гимнастической секции, мы не исключаем того, что этот человек может быть одновременно членом обеих секций.
В языке существует и такое употребление союза «или», при котором этот союз понимается в строго разделительном смысле,
например: «Данный глагол первого или второго спряжения».
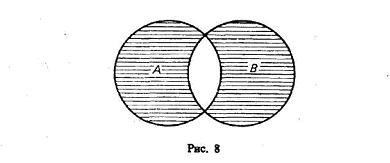
При объединении могут встретиться следующие 6 случаев (рис. 9—14).
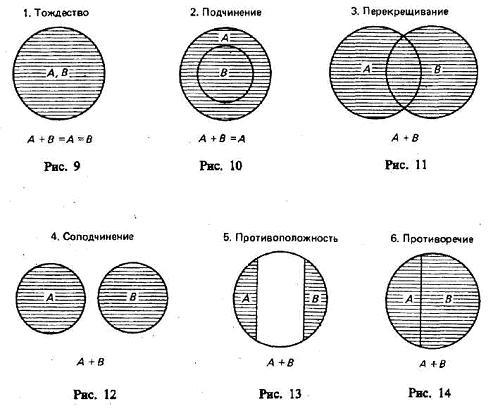
Пересечение («умножение») классов
Общей частью, или пересечением, двух классов называется класс тех элементов, которые содержатся в обоих данных множествах, т. е. это множество (класс) элементов, общих обоим множествам18. Пересечение обозначается или — пустое множество. При пересечении могут встретиться следующие 6 случаев (рис. 15—20, где результат пересечения заштрихован).
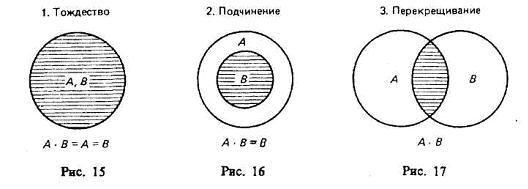
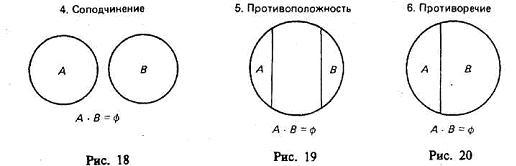
Основные законы логики классов. Законы операций объединения и пересечения
1. Законы идемпотентности.
А + А = А. А х А = А.
В школьном курсе алгебры таких законов нет. В логике первый из этих законов означает следующее. Если мы к классу «дом» прибавим класс «дом», то получим класс «дом», т. е. домов не станет в два раза больше и объем понятия «дом» останется прежним.
2. Законы коммутативности. Эти законы существуют в алгебре, в арифметике, в теории множеств и в логике классов.
А + В = В+А. А В=В А.
Если мы к классу «растение» прибавим класс «животное», то получим класс «организм»; тот же самый класс получим, если мы к классу «животное» прибавим класс «растение».
3. Законы ассоциативности. Они существуют в арифметике, алгебре, теории множеств и в логике классов.
(А+В) + С = А + (В+С). (A х B) х C=A х (B х С).
4. Законы дистрибутивности.
(A+B)C=(A х С)+(B х С). (A х B) + C=(A + С) х (B+С).
5. Законы поглощения. Этих законов нет в арифметике и в школьном курсе алгебры.
А + (А х В)=А. А х (А+В)=А.
Доказательство этих законов осуществляется графическим методом.
Вычитание классов
Рассмотрим два множества (класса) А и В, из которых В может и не быть частью А. Разностью множеств (классов) А и В называется множество тех элементов класса А, которые не являются элементами класса В. Разность обозначается А —В.
Могут встретиться следующие пять случаев (если классы А и В не пусты и не универсальны).
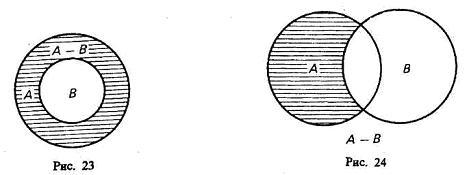
1-й случай (рис. 23). Класс А включает в себя класс В. Тогда разностью А — В будет заштрихованная часть А, т. е. множество тех элементов, которые не суть В. Например, если мы из множества звуков русского языка (А) вычтем множество гласных звуков (В), то получим множество согласных звуков, изображенное на чертеже в виде заштрихованного кольца.
2-й случай (рис. 24). Разностью двух перекрещивающихся классов будет заштрихованная часть А. Например, разность множеств «рабочий» (А) и «рационализатор» (В) даст множество рабочих, которые не являются рационализаторами.
3-й случай (рис. 25). Если класс А полностью включен в класс В и класс В полностью включен в класс А, то эти классы (множества) равны (тождественны). Тогда разность А -В даст пустой, или нулевой, класс, т. е. класс, в котором нет ни одного элемента. Например, если мы из класса «сосна» вычтем класс «сосна», то разность А—В будет равна пустому классу.
4-й случай (рис. 26). Класс А и класс В не имеют общих элементов.
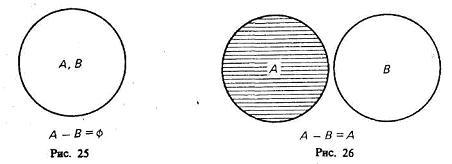
Тогда разность А—В=А, так как всякий элемент класса А не является элементом класса В. Например, разность класса «стол» (А) и класса «стул» (В) равна классу «стол» (А).
В результате «вычитания» классов, соответствующих понятиям, находящимся в отношении противоположности [«низкий дом» (А), «высокий дом» (В)] или противоречия [«одушевленный предмет» (А), «неодушевленный предмет» (В)], разность А— В также равна А (рис. 27, 28).
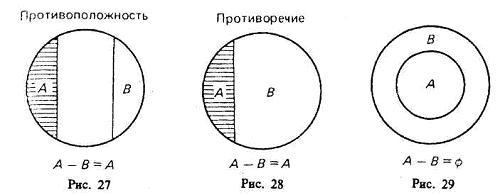
5-й случай (рис. 29). Если объем класса А меньше объема класса В, то в результате вычитания получим пустой класс, так как нет элементов класса А, которые не являлись бы элементами класса В. Например, разность класса «личное местоимение» (А) и «местоимение» (В) дает пустой класс.
Для операции вычитания классов справедливы следующие законы:
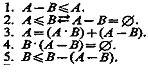
В интерпретации логических алгебр посредством классов запись обозначает включение класса А в класс В; обозначает эквивалентность классов (А тогда и только тогда, когда В ).
Дополнение к классу А
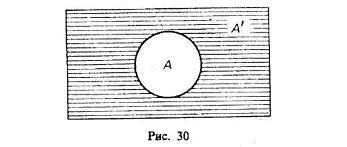
Дополнением к классу А называется класс А" который, будучи сложенным с А, дает рассматриваемую область предметов (эту область обозначим 1), а в пересечении с классом Адает т. е. для которого Откуда А' = 1- А, поэтому
операцию дополнения к классу А можно рассматривать как частный случай операции «вычитания» (из универсального класса). Если от класса целых чисел (1) отнять класс четных чисел (А), то мы получим класс нечетных чисел (т. е. А" поскольку всякое целое число четное или нечетное и нет таких четных чисел, которые были бы нечетными). Графически это можно изобразить так, что заштрихованная часть будет обозначать дополнение к А, т. е. A' (рис. 30).
операция объединения (сложения) классов А В. Она характеризует объединение двух (или нескольких) классов в один класс, состоящий из элементов слагаемых классов.
Операция вычитания классов дает класс, состоящий из элементов, исключающих элементы вычитаемых классов. Вычитая, например, элементы класса «следователь» (А) из класса «юрист» (В), получаем класс юристов-неследователей
перация пересечения (умножения) классов А В. При проведении такой операции отыскиваются общие элементы для двух или нескольких классов.
образование дополнения (отрицание) А и не-А . Это операция по образованию нового множества путем исключения данного множества из универсального класса, к которому оно принадлежит. Так, исключая множество "студенты-экономисты" (А) из универсального класса понятия "студенты", получаем дополнение (новый класс) (не-А) - "студенты - неэкономисты".
13. Суждение - это такая форма мышления, в которой что-либо утверждается или отрицается о существовании предметов и явлений, о связях между предметами и их свойствами или об отношениях между предметами. Например: «Москва - столица Российского государства», «Петербург не есть столица Российского государства», «Петербург севернее Москвы», «Не существует беспричинных явлений».
С логической точки зрения суждение формируется с помощью понятий. Оно не может существовать без понятий, но и понятие не может быть без суждения, так как в каждом понятии заложена определенная мысль, которая раскрывается через суждение. Но понятие отражает предмет только в существенных признаках, суждение же отражает любые признаки предметов и отношения между предметами. Основная роль понятий - различать предметы в процессе мышления. В суждениях же устанавливаются связи между предметами, формулируются законы, описываются данные опыта. На основе суждений, отражающих опыт человеческого общества, вырабатываются новые понятия. Таким образом, с формально-логической точки зрения суждения выполняют в познании роль более высокого порядка, чем понятия.
Всякое суждение может быть истинным или ложным. Истинное суждение - такое, в котором связь понятий правильно отражает реальные свойства и отношения предмета мысли. Например: «Москва - столица России», «Адвокат выясняет условия, способствовавшие совершению преступления», «Некоторые преступления не являются умышленными». Ложное суждение - такое, в котором связь понятий искажает объективные свойства и отношения предмета мысли. Например: «Санкт-Петербург есть столица России», «Адвокат может быть судьей».
Языковой формой выражения суждения является предложение. Суждение есть мысль; предложение - выражение этой мысли словами. Всякое суждение выражается в предложении. Но не всякое предложение выражает суждение. Суждение выражается повествовательным предложением, в котором содержится какое-то сообщение, информация. Например, суждением является мысль «Сегодня идет дождь» и не являются вопрос «Какая сегодня погода?» или восклицание «Противная погода!».
В вопросительных и восклицательных суждениях ничего не утверждается и не отрицается, они не истинны и не ложны. Например: «По какой статье квалифицируется данное преступление?», «Какая наглая ложь!». Однако здесь есть некоторые исключения:
суждение может выражаться так называемыми риторическими вопросами: «И какой же русский не любит быстрой езды?!», где в косвенной форме содержится утверждение. Или: «Как же тебе не стыдно?» - содержится суждение, выражающее уверенность, что «Ты должен этого стыдиться»;
суждения выражаются побудительными предложениями, выражающими воинские приказы, команды, призывы и лозунги. Например, «Ни шагу назад!», «Берегите мир!» выражают так называемые модальные суждения, включающие в себя слово-запрещение и слово-побуждение.
Между суждениями и выражающими их предложениями нет полного совпадения. Одно и то же предложение иногда выражает два и более различных суждения. Например, предложение «Он сочиняет» можно понять и как «Он занимается работой над каким-либо письменным произведением», и как «Он лжет».
С другой стороны, одно и то же суждение может быть выражено двумя и более разными предложениями. Например, «Человек смертен» и «Человек всегда рано или поздно умирает» - два предложения, выражающие совершенно одну и ту же мысль. В живой речи очень часто одна и та же мысль выражается разными предложениями для того, чтобы избежать однообразия. Но иногда человек, повторяя на разные лады одну и ту же мысль, думает, что «доказывает» ее. Слушатель тоже легко может принять такой прием за доказательство. Поэтому очень важно научиться быстро отличать суждения от предложений и равнозначные суждения (выражающие одну и ту же мысль) от неравнозначных.
Суждение, являясь формой мышления, имеет свою внутреннюю структуру. По составу суждения бывают простые и сложные.
|
ПРОСТОЕ |
СЛОЖНОЕ |
|
Простым суждением является суждение, ни одна логическая часть которого не является суждением. Например, кража (S) есть преступление (Р) S есть Р |
Сложным является суждение, какая- либо логическая часть которого является суждением. Кража (S1) и разбой (S2) относятся к умышленным преступлениям Р (S1 есть Р) л (S2 есть Р) |
Рассмотрим логическую структуру простых суждений. Элементами логической структуры простого суждения являются:субъект, предикат, связка и квантор.
1.Логическое подлежащее (субъект) - то, о чем говорится в суждении. Обозначается буквой S (от лат. subjection - лежащий в основе).
2.Логическое сказуемое (предикат) - то, что мыслится о субъекте суждения. Обозначается буквой Р (от лат. predicatum -сказанный).
3.Связка (союз) - та часть суждения, которая выражает связь между субъектом и предикатом. Она характеризует принадлежность предмету мысли какого-либо свойства, отраженного в предикате, или его отсутствие. Обычно выражается знаком «тире» или словами «суть» («есть» и «не есть», «является» и «не является»). Например: «Преступление есть общественно опасное деяние» и «Некоторые деяния не являются преступлениями». Состав простого суждения можно выразить общей формулой
S есть (не есть) Р
4. Кванторы - символы , - указывающие, относится признак, выраженный в предикате суждения, ко всему объему или к части объема понятия, выражающего субъект. Квантор находится перед субъектом и обозначается кванторными словами «все», «некоторые», «ни один» и др. Однако в некоторых суждениях квантор может отсутствовать.
Чтобы легче было установить структуру (логическую форму) суждения, надо иногда перестроить его, совершенно не стесняясь того, что обороты речи будут непривычными и режущими слух. Например: суждение «Он пишет» надо преобразовать в суждение «Он (S) есть пишущий (Р)». Или: «Все слушатели первого курса (S) изучают логику (Р)» преобразовать в суждение «Все слушатели первого курса есть изучающие логику».
Сложные суждения состоят из двух или более простых суждений, соединенных логическими союзами.
14. К простым суждениям относятся такие, которые выражают связь двух понятий и имеют структуру:
S есть (не есть) Р.
Простым считается суждение, у которого лишь один субъект и один предикат. Причем, суждение останется простым и в том случае, если к одному субъекту (предикату) относится несколько предикатов (субъектов). Например, суждение «Лимонад, минеральная вода, кофе, чай – напитки» будет простым суждением со сложным субъектом, а суждение «Зеленый чай утоляет жажду, повышает тонус, способствует оздоровлению организма» окажется простым суждением со сложным предикатом.
В зависимости от того, что утверждается или отрицается в простых суждениях: принадлежность признака предмету, отношение между предметами или факт существования предмета, – они делятся на атрибутивные, суждения с отношениями, экзистенциальные.
1. Суждения, в которых признак предмета приписывается (или отрицается) предмету, называются атрибутивными суждениями или суждениями о принадлежности каких-либо признаков (атрибут – признак) предметам (суждения свойства). Поскольку наличие или отсутствие признака не ставится под какое-либо сомнение, т.е. утверждается категорически, такие суждения в традиционной логике называются простыми категорическими. Например: «Никто из судей не вправе воздерживаться от голосования». «Франция – демократическое государство», «Все рыбы дышат жабрами», «Некоторые птицы не летают». С подобными суждениями чаще всего работает логика.
2. Суждениями с отношениями. В этих суждениях утверждаются те или иные отношения между предметами(пространственные, временные, причинно-следственные и т.д.). Например: «Саратов расположен севернее Волгограда». «Земля больше Луны», «Паровая машина изобретена раньше электрической», «Спокойствие души важнее сытости тела».
3. Простые суждения могут быть экзистенциальными или суждениями существования. В них выражается факт существования (или не существования) предмета. Например: «Не существует беспричинных явлений». «Казань расположена на Волге», «у природы (есть) много загадок», «внеземные
цивилизации не существуют». Эти суждения обладают небольшой познавательной ценностью, поскольку в такой форме обычно выражаются общеизвестные факты и те сведения, которые можно найти в словарях и справочниках.
4. В случае если суждения содержат дополнительную информацию, они называются модальными. В их составе присутствует модальный оператор (доказано, запрещено, необходимо, верю, хорошо, плохо и т.д.). Например: «Как хорошо, что сегодня прохладно», «Давно доказано, что употребление пива подростками повышает риск алкогольной зависимости», «Каждый гражданин обязан уважать законы государства». Модальные суждения являются предметом модальной логики.
В рассуждениях могут использоваться суждения, предикат которых относится не к одному, а к двум или более субъектам, например: «Студенты и школьники являются учащимися». Это суждение является сложным, состоящим из двух простых: «Студенты являются учащимися» и «Школьники являются учащимися». Но так как все два суждения имеют один и тот же предикат, оно может рассматриваться как простое, имеющее сложный субъект. Иногда суждения отражают принадлежность предмету нескольких признаков. Например: «На перемене студенты пили кофе и ели пирожное». Это суждение является сложным, состоящим из двух простых, но его можно рассматривать как простое с одним сложным предикатом.
Атрибутивные суждения называются в традиционной логике категорическими суждениями, так как они выражаются в безусловной, не допускающей иных толкований, форме. С точки зрения качества связки категорические суждения делятся наутвердительные и отрицательные. В утвердительных суждениях логическая связка («есть») приписывает предикат субъекту, например: «Человек есть животное». В отрицательных суждениях логическая связка отделяет предикат от субъекта.
С точки зрения объема субъекта категорические суждения делятся на единичные, частные и общие. В единичных суждениях объем субъекта состоит из одного элемента, например: «Иванов сдал экзамен».
В частных суждениях содержание предиката относится только к части элементов объема субъекта. Например, «Некоторые российские граждане являются студентами».
В общих суждениях предикат относится ко всем элементам объема субъекта. Например: «Все студенты нашей группы пришли на лекцию».
Объединенная классификация по качеству и количеству совмещает в себе деление суждений по качеству и количеству. В ней высказывания делятся на четыре группы:
1) общеутвердительные суждения (утвердительные по качеству связки и общие по объему субъекта) традиционно обозначаемые символом «А». Общеутвердительными будут не только суждения, в которых говорится в целом о какой-то группе предметов (Каждый чемпион мира – выдающийся спортсмен»), но и так называемые единичные суждения (Чехов – писатель, написавший «Вишневый сад»), поскольку субъект в них тоже берется в полном объеме.
Формула: Все S есть Р;
2) общеотрицательные суждения (отрицательные по качеству связки и общие по объему субъекта). Символ, обозначающий такое суждения «Е» («Ни один ребенок не способен к длительному сосредоточенному вниманию»).
Формула: Ни одно S не есть Р ;
3) частноутвердительные (утвердительные по качеству связки и частные по объему субъекта), его символ «I» («Некоторые герои древности были греками»)
Формула: Некоторые S есть Р;
4) частноотрицательные (отрицательные по связке и частные по объему субъекта) обозначается символом «О» («Многие конфликты не являются неизбежными»).
Формула: Некоторые S не есть Р.
Выделяющий называется суждение, отражающее факт принадлежности (непринадлежности) признака только данному предмету. Например: «Только Иванов не сдал экзамен».
Исключающими называются суждения, в которых говорится о принадлежности данного свойства всем предметам данного класса, кроме некоторой их части. Например: «Все студенты данной группы, за исключением Иванова, сдали экзамены». Исключающие суждения выражаются предложениями со словами «за исключением», «кроме», «не считая» и т. д.
Термин называется распределенным в том случае, если он в суждении берется в полном объеме.
Если термин в суждении берется не в полном объеме, то он является нераспределенным.
Правило распределенности терминов: Субъект распределен в общих суждениях и нераспределен в частных, предикат распределен в отрицательных и, как правило, нераспределен в утвердительных суждениях.
Логические отношения устанавливаются только между сравнимыми суждениями, т. е. имеющими общий смысл высказываниями.
Сравнимыми являются суждения, имеющие одинаковые термины, – «субъект» и «предикат». Например: «Все россияне имеют право на образование» и «Некоторые россияне не имеют право на образование». Такие суждения можно сравнивать по истинности, ибо они имеют одинаковые термины.
Несравнимыми высказываниями являются такие, которые имеют различные термины. Например: «Все россияне имеют право на образование» и «Все граждане Украины имеют право на образование» У этих суждений хотя и одинаковы предикаты, но различны субъекты, поэтому между ними нельзя установить логическую зависимость.
Между общеутвердительными (А), общеотрицательными (Е), частноутвердительными (I) и частноотрицательными (О) суждениями с одинаковыми терминами существует четыре вида отношений:
1) отношение подчинения;
2) отношение контрадикторности;
3) отношение контрарности;
4) отношение субконтрарности.
Для облегчения подготовки данного вопроса рекомендуется использовать логический квадрат (см. рис. 10).
Отношения между простыми суждениями обычно рассматривают при помощи известной еще со времен Средних веков схемы, называемой логическим квадратом. Вершины этого квадрата символизируют простые категорические суждения определенного вида, а стороны и диагонали – отношения между суждениями.
Среди сравнимых различают совместимые и несовместимые суждения.
Совместимыми являются суждения, которые одновременно могут быть истинными.
Различают три вида совместимости: эквивалентность (полная совместимость), частная совместимость (субконтрарность) и подчинение.
Эквивалентными являются такие суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.
Различия между высказываниями, содержащими эквивалентные суждения, проявляются, главным образом, в языке. Например: использование синонимов для выражения субъекта и предиката, выражение суждения на различных языках («Это стол», «Es ist Tisch»).
Частичная совместимость возникает у суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными. Например: при ложности суждения «Некоторые студенты пришли на семинар» будет истинным суждение «Некоторые студенты не пришли на семинар».
Отношение подчинения между суждениями имеет место в том случае, когда при истинности одного из них – подчиняющего другое – подчиненное всегда будет истинным. Например, при истинности суждения «Все студенты пришли на семинар» всегда будет истинным и подчиненное ему суждение «Некоторые студенты пришли на семинар».
Несовместимыми являются суждения, которые одновременно не могут быть истинными.
Различаются два вида несовместимости: противоположность и противоречивость.
15.
Под модальностью в формальной логике понимают выраженную в суждении дополнительную оценочную информацию о связях между явлениями, о логическом статусе суждения, о регулятивных, временных и других его характеристиках.
В модальном суждении явно или неявно используется модальный оператор: «возможно», «необходимо», «доказано», «плохо», «запрещено» и т. д. Например: «Плохо, когда студент пропускает занятия по неуважительной причине». Структура этого суждения такая: М (S есть Р). В широком смысле слова любая дополнительная информация в суждении называется модальностью данного суждения.
Существует большое разнообразие модальностей, которые разделены на классы. Но мы рассмотрим только вида модальностей, которые считаются наиболее часто употребляемыми в познавательном процессе: алетическую, эпистемическую и деонтическую.
I. Алетическая модальность («алетический» – слово греческого происхождения, означает «истинный») – это выражаемая с помощью операторов «необходимо», «случайно», «возможно», «невозможно» информация о логической либо фактической обоснованности суждения: «Возможно завтра будет солнечный день»; «Невозможно, чтобы человек в своей жизни никогда не ошибался».
В символической логике алетическая модальность обозначается следующим образом: «€ А» – «необходимо A»; « A» – «случайно А»; « А» – «возможно А»; «~ А» – «невозможно А».
Суждения бывают ложными или истинными в силу некоторых факторов, которые можно разделить на две части: фактические и логические. Это определяет соответствующие типы модальностей: фактическую модальность и логическую модальность.
Фактическая модальность связана с объективной обусловленностью суждений, когда их истинность и ложность определяются реальным положением дел в окружающей действительности.
К фактически истинным относятся суждения, в которых связь между терминами суждения соответствует действительным отношениям между явлениями. Пример такого суждения: «КГУ находится в Казани».
К фактически ложным относятся суждения, в которых связь между субъектом и предикатом не соответствует реальности: «КГУ находится в Берлине». Поэтому здесь следует использовать модальный оператор: «Неверно, что КГУ находится в Берлине».
Использование модальных понятий необходимости и случайности, возможности и невозможности происходит при выражении действительных связей между явлениями. Фактическую модальность, в свою очередь, можно разделить на фактически необходимую, фактически случайную, фактически возможную и фактически невозможную виды.
Фактически необходимые – это суждения, в которых говорится о связи явлений, определяемой их устойчивой внутренней основой и совокупностью условий их развития. Таковыми являются научные законы. Например: «Во всех инерциальных системах все механические процессы происходят одинаковым образом». В естественном языке фактически необходимые суждения часто выражают с помощью слов «обязательно», «непременно», «необходимо» и т. п.
Например: «Вода непременно закипит при 100 градусах Цельсия при нормальных условиях». Все остальные фактические суждения относятся к случайным.
Фактически случайные – это суждения, в которых говорится о связи, определяемой внешними, побочными для данного явления причинами. К случайным относятся суждения, которые не являются необходимыми. Их истинность и ложность определяются конкретными условиями, имеющими единичный характер. Например, суждение «Великая Отечественная война началась 22 июня 1941 года» является фактически случайным, ибо война могла начаться как до, так и после этой даты. Как известно, Гитлер неоднократно откладывал начало военных действий.
Фактически возможные – это суждения, содержащие информацию о единой основе развития явлений. Например: «В Волгограде сегодня, может быть, пойдет дождь». В естественном языке показателями суждений возможности являются следующие слова: «возможно», «может быть», «допускается». Они употребляются в качестве вводных слов, сказуемых.
Фактически невозможные – это суждения, содержащие информацию об отсутствии единой основы развития явлений.Например: «Обучение на юридическом факультете КГУ невозможно для человека, не имеющего среднего образования».
Логическая модальность – это информация об обусловленности суждения, которая основывается на законах и правилах логики. В нем истинность или ложность определяется структурой суждения. К ним, например, относятся суждения, выражающие законы логики (закон тождества: Всякая мысль в процессе рассуждения должна быть тождественна самой себе). К логически ложным относят внутренне противоречивые суждения. Например: «Я так тебя люблю, что ненавижу».
II. Эпистемическая модальность – это выраженная в суждении информация обосновании и степени его достоверности(«эпистема» означала в античной философии высший тип несомненного, достоверного знания).
Операторы таких суждений: доказуемо, недоказуемо, неразрешимо, опровержимо.
Общение между людьми предполагает использование различных оценок и фактических данных, имеющих разную степень достоверности, которая зависит от многих условий. Важнейшими среди них являются логические и нелогические условия, предопределяющие два эпистемических типа суждений: рационально обоснованные суждения, выражающие знание, и основанные на вере суждения, имеющие иррациональный характер.
Ориентированное на логику познание предполагает принятие в качестве истинных лишь таких суждений, которые опираются на достоверно установленные эмпирическим или теоретическим путем данные.
В логике по степени обоснованности различают два класса суждений: достоверные (например, таковым можно считать суждение «Правильно, что живые организмы являются огромной геологической силой, как аргументировано доказал В.И. Вернадский») и проблематичные (например, «По-видимому, жизнь существует не только на Земле»).
Достоверное суждение – это такое высказывание, в котором содержится твердо установленная информация.Суждения, истинность которых обоснована, служат в познании в качестве исходного пункта новых логических выводов, приводящих к дальнейшему расширению достоверного знания. Достоверные суждения следует отличать от проблематичных.
Проблематичные суждения – это такие высказывания, которые нельзя считать достоверными в силу того, что истинность или ложность таких суждений точно не установлена. Они лишь претендуют быть истинными. Поэтому необходимо разрешить проблему: является ли содержащаяся в суждении информация достоверной? Поэтому их назвали проблематичными. В естественном языке в таких высказываниях обычно используют такие вводные слова, как «вероятно», «по-видимому», «возможно» и др.
К нелогическим факторам, которые воздействуют на человека, «заставляя» его признавать те или иные суждения в качестве истинных или ложных, можно
отнести следующие: прагматический интерес, традиции, мнение авторитетов, внушение и т. п. По эпистемическому положению любые суждения, обоснованные верованием, отличаются иррациональным и эмоциональным, без критического анализа их принятием субъектом. Несмотря на их иррациональность, они могут быть с социальной точки зрения прогрессивными, но чаще они носят реакционный характер.
III. Деонтическая модальность (слово «деонтический» означает в греческом языке «обязанность») – это выраженная в суждении информация, побуждающая людей к определенным поступкам. В естественном языке высказывание строится в форме совета, пожелания, команды, правила поведения или приказа. В таких суждениях часто присутствуют операторызапрещено, разрешено, имеет право, обязан, должен. Например: «Лекции по логике желательно слушать с большим вниманием»; «Не рекомендуется пропускать семинарские занятия по логике». «Граждане нашей страны имеют право на отдых; запрещено посещать библиотеку без читательского билета»; «В нашей стране разрешено получать паспорт с 14-ти лет, а водительские права – с 18-ти».
IV. Аксиологическая модальность. Операторы суждений: хорошо, плохо, превосходно. «Хорошо, что завтра выходной». «Превосходно, что в наш офис установили еще один компьютер». «Плохо, что сегодня я задержался на работе до позднего вечера».
V. Временная модальность. Операторы: всегда, никогда, одновременно, раньше, позже. «Всегда можно найти выход из сложной ситуации». «Раньше я любил бродить по тихим улочкам и мечтать». «Никогда не вороши прошлое».
16 Суждения, которые образуются из простых суждений при помощи логических союзов, называются сложными.
Основными логическими союзами являются:
конъюнкция – логические союзы «и», «а», «но», «как», «так и», «так же» имеют чисто соединительное значение, Символически такие суждения обозначаются так: pÙq, где p,q – простые суждения, входящие в состав сложного. Например, родители дают обещание своему ребенку «в воскресенье мы пойдем в кино, а вечером папа купит тебе мороженное»; или другой пример «он сдал все экзамены, но еще не защитил диплом»;
неисключающая (слабая) дизъюнкция (обозначается формулой pÚq) – логический союз «или» имеет соединительно-разделительное значение, союз «или» имеет соединительно-разделительное значение, не придает исключающего смысла входящим в сложное суждение составляющим, например, «Я подарю ей цветы или конфеты»; «Он будет цитировать Толстого или Чехова» и исключающая (сильная) дизъюнкция – логический союз «либо... , либо...» имеет чисто разделительное значение, например, «Я полечу на Юг на самолете или поеду на поезде»; «Я куплю новую квартиру или перееду жить к своей сестре».
импликация или условное суждение – логический союз «если..., то...» каким-то образом (не обязательно по смыслу) соединяет два суждения, связанные между собой (грамматический союз «если..., то...», в отличие от логического, объединяет предложения обязательно связанные по смыслу), В таких суждениях выражаются причинные, временные, функциональные, пространственные, зависимости, разрешения, предписания, запреты и т.д. Символически такие суждения изображаются так: p®q. «Если будет хорошая погода, мы пойдем в лес»;
эквивалентность – логический союз «тогда и только тогда, когда...» («если и только если...») объединяет два суждения, связанные однозначной зависимостью. Иногда его называют двойной импликацией, поскольку простые суждения, входящие в состав сложного связаны взаимной зависимостью «если и только если», «тогда и только тогда», «там и только там», «лишь при условии» и т.д.
Вид сложного суждения определяется по главному логическому союзу: если главным логическим союзом в данном суждении является конъюнкция, то это конъюнктивное суждение, дизъюнкция – дизъюнктивным и т. д.
Необходимо различать грамматическое и логическое значение перечисленных выше союзов. Логическое значение этих союзов задается с помощью таблицы истинности.
Таблица 1. Условия истинности сложных суждений
|
Первое простое суждение |
Второе простое суждение |
Конъюнкция |
Слабая дизъюнкция |
Сильная дизъюнкция |
Импликация |
Эквивалентность |
|
истинное |
истинное |
истинное |
истинное |
ложное |
истинное |
истинное |
|
истинное |
ложное |
ложное |
истинное |
истинное |
ложное |
ложное |
|
ложное |
истинное |
ложное |
истинное |
истинное |
истинное |
ложное |
|
ложное |
ложное |
ложное |
ложное |
ложное |
истинное |
истинное |
17. Между понятиями с различными объемами и содержанием складываются разные отношения. Рассмотрение этого вопроса позволяет дисциплинировать мышление и достичь большей четкости в высказываниях. Кроме того, этот вопрос пригодится в дальнейшем, при рассмотрении темы «Суждение».
Итак, сравнивать между собой можно только понятия, у которых есть хотя бы один общий признак. В отличие от таких, сравнимых, понятий, несравнимые не имеют общих признаков и в отношения друг с другом не вступают. Традиционно объемы понятий изображаются кругами Эйлера разного диаметра. Так вот, в случае несравнимых понятий эти круги будут рисоваться совершенно отдельно, не соприкасающимися друг с другом.
Сравнимые по содержанию и объему понятия делятся на совместимые и несовместимые. Совместимые не имеют взаимоисключающих признаков, их объемы частично или полностью совпадают. Объемы несовместимых понятий совсем не совпадают, поскольку эти понятия имеют взаимоисключающие признаки. И совместимые, и несовместимые понятия делятся, в свою очередь, на группы. Для совместимых понятий это а) соразмерные, б) подчиненные, в) перекрещивающиеся. Среди несовместимых понятий выделяют а) соподчиненные, б) противоположные, в) противоречащие.
Соразмерные (равнообъемные, равнозначные), а попросту тождественные это понятия объем и содержание которых полностью совпадает. Это, в первую очередь, синонимы (карлик-лилипут, бегемот-гиппопотам и т.д.), а также имена собственные и указание на их уникальные признаки (Адам – первый человек, Эйнштейн – создатель теории относительности). Соразмерные понятия изображаются одним кружочком, но внутри его две буквы латинского алфавита, указывающие, что понятий два (их может быть и больше, если большим является ряд синонимичных понятий).
Эта схема читается так: всякий А есть В и всякий В есть А.
Подчинение (субординация) – отношение между понятиями по принципу «род-вид-индивид». Объем подчиняющего понятия (род) включает в себя объем подчиненного (вид), которое, в свою очередь, может включать объем следующего понятия (индивид). Например, спортивная игра – настольная игра – шахматы, наука – теоретическая наука – философия. Именно к таким понятиям относится закон обратного отношения между объемом и содержанием понятий. Изображаются такие понятия кружком в кружке.
Читаться такая схема будет следующим образом: всякий В есть А, но не всякий А есть В. Так, любой студент – учащийся, но не всякий учащийся студент, любой анекдот есть народное творчество, но не всякое народное творчество анекдот, всякая кража – преступление, но не всякое преступление – кража.
Перекрещивание или частичное совпадение объемов при различном содержании встречается в тех случаях, когда перед нами понятие, каждое из которых обладает своим особым набором признаков, однако эти признаки не взаимоисключают друг друга. Поэтому при определенных условиях объемы таких понятий могут совпадать. Так, понятия школьник и спортсмен – это самостоятельные понятия, обладающие своими особыми признаками. Но ведь ничто не мешает школьнику заниматься еще и спортом. Поэтому эти понятия будут перекрещиваться, между ними будет «общее поле» (на рисунке оно заштриховано), на котором и расположатся школьники спортсмены.
Читается такая схема так: некоторые А есть В, некоторые В есть А, но А и В разные понятия.
Перейдем к несовместимым понятиям. Соподчинение (координация) – отношение понятий, объемы которых взаимно исключают друг друга, но, благодаря тому, что у них есть хотя бы один общий признак они включаются в объем более широкого, родового, понятия, видами которого являются. Что общего между самокатом, самосвалом и авиалайнером? Нет, с логической точки зрения это не колеса, а то, что все они – средства передвижения. Точно так же майор, рядовой и генерал объединены одним общим признаком – они военнослужащие. Схема соподчиненных понятий: несколько кружочков (по числу понятий), заключенных в больший по объему общий круг Эйлера.
И, наконец, противоположные (контрарные) понятия, представляющие собой крайние значения соподчиненных понятий одного рода. Каждое из них отрицает другое, но при этом обладает своими особыми, специфическими признаками, которыми заменяет признаки отрицаемого понятия: белый – черный, высокий – низкий, кроха – великан. Они располагаются на различных полюсах значений и соответственно в разных сторонах кругов Эйлера, и в сумме составляют лишь часть объема подчиняющего понятия.
Противоречащие (контрадикторные) – это понятия одного рода, одно из которых полностью отрицает признаки другого, не заменяя их никакими другими: сладкий – не-сладкий, большой – не-большой, книга – не-книга…Сумма противоречащих понятий исчерпывает объем подчиняющего понятия полностью.
18. умозаключение – это форма мышления, посредством которой из одного или нескольких определений, истинность которых доказана, с необходимостью выводится суждением, несущее новое знание. Структура умозаключения содержит посылки и вывод или заключение.
Посылки – это суждения, из которых делается вывод. Они содержат известное знание и должны быть истинными.Вывод (заключение) – новое суждение, полученное из посылок в ходе умозаключающей деятельностиИз суждений составляется более сложная и важная в теоретическом отношении форма логического мышления - умозаключение. Иногда к ним прилагают название "силлогизм", хотя, строго говоря, силлогизм - только одна из разновидностей умозаключения, правда, наисложнейшая и, пожалуй, самая распространенная. С помощью умозаключения мысли, выражаемые через суждения, связываются между собой, образуя новую мысль, которую можно рассматривать результатом их сцепления, взаимодействия. Возьмем для наглядности такое рассуждение:
Если число 64 делится на 3 и на 4, то оно делится на 12.
Число 64 не делится на 12.
Следовательно, число 64 не делится на 3 или на 4.
Это так называемая усложненная контрапозиция. При такой схеме рассуждения из высказываний, составляющих первые две строчки, с необходимостью вытекает третье (третья строчка). Мы могли бы взять и какие-то другие явления, связанные подобным же образом, например: если дует сильный ветер и падает снег, то значит на улице пурга; но пурги нет; следовательно, на улице не падает снег или нет ветра.
Умозаключение - это форма мышления, позволяющая из одного или нескольких суждений, называемых посылками, извлекать с помощью правил логики новое суждение - заключение.
Когда исходные высказывания в правильно построенном умозаключении истинны, то и вывод его тоже обязательно будет истинным суждением.
Понятия и суждения как формы мышления формируются большей частью за пределами логики, которая берет их уже готовыми. Умозаключение же формируется из суждений именно по логическим правилам.
На стадии умозаключения о вещах можно рассуждать, не обращаясь к ним самим. Достаточно иметь о них несколько верных высказываний. По этой причине, опираясь на правила умозаключения, наука получает возможность рассуждать о природных явлениях теоретически, постигать те их стороны, которые скрыты за внешней, доступной наблюдению поверхностью, проникать в недоступные природные глубины, обращаться мыслью в такие запредельные дали, которые можно изучать лишь умозрительно. Палеонтологам иной раз хватает одной кости для воссоздания всего облика давно вымерших животных. Сходные достижения имеются во всех других науках. Например, Демокрит догадался о существовании атомов, наблюдая, как истираются со временем каменные ступени храма. Много великих и малых тайн природы разгадано благодаря тонким и сложным рассуждениям. Цепь умозаключений выстраивается порой в целые обширные теории.
Всю совокупность известных логике умозаключений принято классифицировать по двум основаниям: во-первых, по числу посылок, во-вторых, по направлению движения мысли. Что касается числа посылок, то с этой точки зрения весь их массив распадается на две неравновесные части, те, у которых посылка всего одна, и остальные. Первые называются непосредственными умозаключениями. Они относятся к наиболее простым их разновидностям. В них происходит простая смена логической формы того или иного высказывания, содержание же остается неизменным. Помимо самой посылки в таком преобразовании участвуют также и логические законы мышления. Во вторых, опосредствованных, умозаключениях посылок более одной, они сложнее и многообразнее первых.
По другому основанию умозаключения делят на дедуктивные, в которых мышление движется от общих положений к частным выводам, индуктивные, делающие обобщения из частных наблюдений, и такие, у которых уровень общности посылок и заключения одинаков; к ним, прежде всего, относится аналогия и некоторые суждения с отношениями; иногда последнюю группу объединяют под названием традуктивные умозаключения.
ВИДЫ УМОЗАКЛЮЧЕНИЙ:
|
По количеству посылок |
По характеру посылок и связок |
По направлению мысли |
|
Непосредственные - Дедуктивные - Индуктивные - Традуктивные (по аналогии) |
- Категорические - Разделительные - Условные - Разделительно-категорические - Условно-категорические - Условно-разделительные |
- Дедуктивные - Индуктивные - Традуктивные |
19.20.21. В логике существует два подхода к определению дедукции.
В традиционной (аристотелевской) логике под дедукцией понимают переход от общего знания к частному.
В символической логике дедукция – это умозаключение, дающее истинное суждение (Далее этот термин будет использоваться в традиционном толковании).
Дедуктивные умозаключения в зависимости от количества исходных посылок делятся на непосредственные и опосредованные.
Умозаключение, полученное посредством преобразования одного суждения, называется непосредственным.
Если же в нем две или больше посылки, то это опосредованное умозаключение.
В формальной логике выделяют следующие виды непосредственных умозаключений: превращение, обращение, противопоставление предикату и умозаключение по логическому квадрату.
Превращение – это логическая операция, посредством которой суждение преобразуют в суждение, противоположное по качеству, с предикатом, противоречащим предикату исходного суждения. Например: «Петров является учащимся». («Петров не является не учащимся»). S есть Р (S не есть не-Р). Иными словами, утвердительные суждения превращаются в отрицательные, а отрицательные в утвердительные, при этом предикат изменяется на противоречащее ему понятие. Это бывает необходимо, когда необходимо, например, уточнить те или условия, в которых предикат действительно относится к субъекту. Например, если написано: «к экзаменам допускаются лица, имеющие аттестат о среднем образовании». А только ли они? И нельзя ли участвовать тем, кто такого аттестата не имеет? Обычно автоматически в таких случаях проделывается превращение: «к экзамену не допускаются лица, не имеющие аттестата о среднем образовании».
Главное в превращении, как и в любом другом непосредственном умозаключении, чтобы смысл исходного суждения не пострадал, он может быть лишь уточнен. А для этого существует правило превращения: двойное отрицание равносильно утверждению. Совсем как в математике. При этом существует разница в превращении утвердительных и отрицательных суждений. В первом случае двойное отрицание распределяется так: перед связкой и перед предикатом. Например: Все (некоторые) S есть P превращается в Ни одно (некоторые) S не есть не–P.
В отрицательных суждениях, где связка уже изначально отрицательная, это самое отрицание переносят к предикату. В этом случае получается следующая картина: Ни одно (некоторые) S не есть P превращается в суждение Все (некоторые) S есть не-P.
Превращать можно любое суждение. Общеутвердительное суждение превращается в общеотрицательное («Все студенты нашей группы являются
гражданами РФ. Следовательно, ни один студент нашей группы не является не гражданином РФ»), общеотрицательное в общеутвердительное («Все волки не являются травоядными животными. Следовательно, все волки являются нетравоядными животными»), частноутвердительное в частноотрицательное («Некоторые государства являются унитарными. Следовательно, некоторые государства не являются неунитарными»), а частноотрицательное превращается в частноутвердительное («Некоторые животные не являются кошками. Следовательно, некоторые животные являются не кошками»).
Обращение – это логическая операция, посредством которой происходит преобразование суждения, в результате которого субъект исходного суждения становится предикатом нового суждения предикат – субъектом. Например: «Все выпускники юридического факультета КГУ изучали логику. Следовательно, не которые изучавшие логику – выпускники юридического факультета КГУ».
В процессе операции обращения необходимо подчиняться следующему правилу: Термин, нераспределенный в посылке, не должен быть распределен в заключении. (Распределенный термин – это термин, взятый в полном объеме).
Если в процессе обращения количественная характеристика остается такой же, то это обращение называю простым(чистым). Например: «Некоторые студенты нашей группы – отличники. Следовательно, некоторые отличники – студенты нашей группы».
В тех случаях, когда количественная характеристика в результате логической операции меняется, то такое обращение называется обращением с ограничением. Например: «Все россияне имеют право на социальную защиту. Следовательно, некоторые имеющие право на социальную защиту – россияне».
Общеутвердительное суждение, в котором субъект распределен, а предикат не распределен, обращается в частноутвердительное, т. е. с ограничением (см. пример выше).
Общеотрицательное суждение обращается в общеотрицательное. Например: «Все депутаты Государственной Думы не могут быть подвергнуты административному наказанию. Следовательно, ни один, подвергнувшийся административному наказанию, не может быть депутатом Государственной Думы».
Частноутвердительное обращается в частноутвердительное. Например: «Некоторые студенты нашей группы проживают в центре г. Альметьевска. Следовательно, некоторые проживающие в центре г. Альметьевска отличники – студенты нашей группы».
Частноотрицательное суждение не обращается. Проверим это на примере: некоторые животные не являются хищниками, значит ни один хищник не является животным (???), или все хищники – животные, это столь же абсурдно.
Противопоставление предикату – это логическая операция, посредством которой происходит преобразование суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения. Пример противопоставления предикату суждения: «Все студенты нашей группы любят посещать занятия по логике. Следовательно, ни один человек, не любящий посещать занятия по логике, не является студентом нашей группы».
Необходимо помнить, что противопоставление предикату является результатом превращения и обращения, т. е. данная логическая операция состоит из двух этапов. Сначала из суждения выводят заключение путем превращения, затем из этого заключения делают вывод путем обращения. В итоге мы получаем умозаключение противопоставления предикату.
Путем противопоставления предикату общеутвердительное суждение преобразуется в общеотрицательное. Например: «Все лошади – млекопитающие. Следовательно, ни одна лошадь не является не-млекопитающим и ни одно не-млекопитающее не является лошадью». Еще пример: «Некоторые рабочие не являются фрезеровщиками. Следовательно, некоторые рабочие являются не-фрезеровщиками и некоторые не-фрезеровщики – рабочие». Или: «Ни один экзамен не является зачетом. Следовательно, все экзамены являются не-зачетами и некоторые не-зачеты – экзамены».
Общеотрицательное суждение путем противопоставления предикату преобразуется в частноутвердительное. Например: «Ни один студент нашего курса не имеет двойного гражданства. Следовательно, некоторые имеющие недвойное гражданство – студенты нашего курса».
Частноотрицательное суждение преобразуется в частноутвердительное. Например: «Некоторые студенты не являются совершеннолетними. Следовательно, некоторые несовершеннолетние являются студентами».
Частноутвердительное суждение посредством противопоставления предикату не преобразуется.
Можно строить умозаключения по логическому квадрату, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения (см. рис. 10).
Выводы из отношений контрадикторности:
Аи→Ол; Аи→Ои; Ои→Ал; Ол→Аи; Еи→Iл; Ел→Iи; Iи→Ел; Iл→Еи; Например: Если суждение «Все киты – млекопитающие» (А) истинно, то суждение «Все киты – не млекопитающие» (О) будет ложным (Аи→Ол).
Выводы из отношений контрарности: Аи→Ел; Ал→Е?; Еи→Ал; Ел→А?
Выводы из отношений субконтрарности: Iл→Ои; Iи→О?; Ол→Iи; Ои→I?
Выводы из отношений подчинения: Аи→Iи; Еи→Ои; Iи→А?; Ои→Е; Iл →Ал; Ол→Ел; Ал→I? Ел→О?;
Основным видом опосредованного умозаключения (в нем следствие получают из двух и более посылок) является категорический силлогизм, который представляет собой вид дедуктивного умозаключения, в котором из двух посылок, имеющих общий для них термин, необходимо следует заключение. Простой категорический силлогизм состоит из трех категорических суждений: из двух посылок и заключения.
Понятия, входящие в состав силлогизма, называют терминами силлогизма.
Их всего три: меньший (S), больший (Р) и средний (М).
• Все студенты нашей группы (М) сдали экзамен по философии (P).
Петров (S) – студент нашей группы (М).
Петров (S) сдал экзамен по философии (Р).
• Все М есть Р.
S есть М.
S есть Р.
Меньший термин силлогизма – это понятие, которое в заключении является субъектом; больший – это понятие, которое в заключении является предикатом; средний – это термин, связывающий две посылки, и отсутствующий в заключении.
Посылка, в которую входит меньший термин, называется меньшей посылкой; посылка, в которую входит больший термин, называется большей посылкой.
В формальной логике сформулирована аксиома силлогизма, которая гласит: Все, что утверждается (отрицается) относительно всех предметов данного класса (рода), утверждается (отрицается) относительно каждого предмета этого класса (рода). Другими словами: Все, что мы утверждаем обо всех студентах данной группы (см. пример), также относится и к каждому из них.
Для того чтобы из истинных посылок всегда можно было получить истинное заключение, необходимо соблюдать общие правила категорического силлогизма, три из которых относятся к терминам и четыре – к посылкам.
1-е правило терминов. В каждом силлогизме должно быть только три термина. При нарушении этого правила возникает ошибка учетверения термина. Учетверение чаще всего происходит вследствие употребления омонимов, дающих возможность различного толкования исходных понятий Часто на нарушении этого правила строятся софизмы. Например:
Движение вечно.
Хождение на базар – движение.
Хождение на базар вечно.
2-е правило терминов. Средний термин должен быть распределен хотя бы в одной из посылок. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной. Например:
Некоторые учащиеся (М-) – неуспевающие (Р).
Все студенты (S) – учащиеся (М-).
Все студенты S – неуспевающие (Р).
Здесь средний термин не распределен, поэтому заключение является ложным.
3-е правило терминов. Термин, нераспределенный в посылке, не может быть распределен и в заключении. При нарушении этого правила в заключении говорится больше, чем в посылках. Например:
Все нотариусы (М) имеют юридическое образование (Р-).
Адвокаты (S) – это не нотариусы(ЛГ).
Адвокаты (S) не имеют юридического образования (Р+).
Больший термин (Р) не распределен в посылке, но он распределен в заключении. Поэтому заключение здесь ложное.
Ошибка, связанная с нарушением правила распределенности крайних терминов, называется незаконным расширением меньшего (или большего) термина.
Следующие четыре правила относятся к посылкам.
4-е правило (посылок). Хотя бы одна из посылок должна быть утвердительным суждением, поскольку из двух отрицательных посылок заключение с необходимостью не следует. Средний термин не может установить определенного отношения между крайними терминами, так как они исключаются из него. Например:
Обезьяны – не пресмыкающиеся.
Змеи – не обезьяны.
?
5-е правило (посылок). Если одна из посылок — отрицательное суждение, то и суждение должно быть отрицательным. Например:
Все студенты – учащиеся.
Этот человек – не учащийся.
Этот человек – не студент.
6-е и 7-е правила (посылок) являются производными, вытекающими из рассмотренных 4-го и 5-го.
6-е правило. Хотя бы одна из посылок должна быть общим суждением. Из двух частных посылок заключения с необходимостью не следует. Например:
Некоторые виды обезьян обитают в Африке.
В Красную книгу занесены некоторые виды обезьян.
?
7-е правило. Если одна из посылок – частное суждение, то и заключение должно быть частным.
Все волки – хищные животные.
Это животное – волк.
Это животное является хищным.
В зависимости от положения среднего термина в посылках различают четыре вида категорических силлогизмов, которые в традиционной логике принято называть фигурами силлогизма. В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката.
В первой фигуре средний термин занимает место субъекта в большей и место предиката в меньшей посылке. Она самая распространенная и позволяет сопоставлять частное знание, выраженное в меньшей посылке с общими положениями, содержащимися в большей посылке. Именно таким образом мы строим свои рассуждения, когда нам необходимо уяснить конкретные вопросы на основе имеющегося общего правила
У каждой фигуры есть свои правила. Правила первой фигуры таковы:
1) Большая посылка – общее суждение (А, Е).
2) Меньшая посылка – утвердительное суждение (А, I).
Все студенты (М) нашей группы пришли на лекцию (Р).
Сидоров (S) – студент нашей группы (М).
Сидоров (S) пришел на лекцию (Р).
Попробуйте построить рассуждение, нарушая эти правила, и придете к абсурду. Сравним умозаключение, соответствующее правилам с умозаключением, им не соответствующим:
Все спортсмены – закаленные люди (большая посылка – А)
Некоторые студенты – спортсмены (меньшая посылка – I)
Следовательно, некоторые студенты закаленные люди
Вывод получился частным (некоторые) в соответствии с правилом посылок: если одна из посылок суждение частное, то и вывод будет частным.
А если нарушить правила:
Все спортсмены – закаленные люди (большая посылка – А)
Ни один долгожитель не является спортсменом (меньшая посылка – Е)
Следовательно, ни один долгожитель не является закаленным человеком.
Но это явная ошибка, появившаяся вследствие того, что наличие в качестве меньшей посылки суждения Е противоречит второму правилу I фигуры.
Во второй фигуре средний термин находится на месте предиката в обеих посылках
Такой вариант рассуждений применяется при доказательстве ложности какого-либо положения путем отрицания принадлежности предмета, о котором говорится в меньшей посылке, к тому классу, о котором говорится в большей посылке. Это фигура отрицания, поэтому и выводом из нее всегда бывает отрицательное суждение. А получается оно в соответствии с правилом посылок (если одна из посылок - суждение отрицательное, то и вывод будет отрицательным). Соответственно,правила 2-й фигуры следующие:
1) Большая посылка– общее суждение.
2) Одна из посылок – отрицательное суждение.
Все гадюки (Р) – пресмыкающиеся (М).
Это животное (S) не является пресмыкающимся (М).
Это животное (S) не является гадюкой (Р).
Если поиграть с нарушением этих правил, то из этого может получиться довольно интересное рассуждение. Например, если попытаться сделать вывод из двух утвердительных суждений:
Все собаки имеют уши (суждение А)
Это существо имеет уши (суждение А)
То вывод будет явно опрометчивым: это существо – собака, но он единственно возможный в соответствии с данным ходом рассуждений. Даже если без особых на то оснований в форме приведенных суждений принять во внимание условие, что вывод должен быть отрицательным, нам все равно не удастся избавиться от необоснованности сделанного вывода.
Первая и вторая фигуры считаются самыми распространенными и соответствующими наиболее типичным путям нашей мысли. О третьей и четвертой фигурах этого сказать нельзя, но для полноты картины они всегда рассматриваются в логике, хотя и с оговорками.
Третья фигура симметрична второй: средний термин находится на месте субъекта в обеих посылках.
Правила 3-й фигуры.
1) Меньшая посылка – утвердительное суждение.
2) Заключение – частное суждение.
Пшеница (М) – растение (S).
Пшеница (М) – злак (Р).
Некоторые растения (S) – злаки (Р).
Наконец, симметричная первой, 4-я фигура силлогизма. Средний термин в ней занимает место предиката в большей посылке и субъекта в меньшей
Эта фигура носит искусственный характер, но все же иногда применяется.
Правила 4-ой фигуры:
1) Если большая посылка суждение утвердительное, то меньшая должна быть общей
2) Если одна из посылок суждение отрицательное, то большая должна быть общей.
3) При этом общеутвердительного вывода рассуждения по этой фигуре не дают.
В качестве примера можно привести следующее рассуждение:
Все дельфины (Р) – млекопитающие (М).
Ни одно млекопитающее (М) не есть рыба (S).
Ни одна рыба (S) не есть дельфин (Р).
Пожалуй, каждому ясно, что так «наоборот» мы действительно никогда не рассуждаем.
Каждая фигура имеет свои разновидности в зависимости от того, какие суждения в нее входят. Это модусы. В принципе их может быть 64. Но большая их часть противоречит либо общим правилам силлогизма, либо правилам той или иной фигуры. Поэтому в конечном итоге остается всего 19 модусов: по четыре в первой и второй фигурах, шесть в третьей и пять в четвертой. Они обозначаются тремя латинскими буквами в соответствии с тем, какие именно суждения в них входят (например, АЕЕ или ОАО и т.д.).
22. Силлогизм с пропущенной посылкой или заключением называется сокращенным силлогизмом, или энтимемой1.
Рассмотрим наиболее распространенные виды энтимем. Условно-категорический силлогизм с пропущенной большей посылкой: «Уголовное дело не может быть возбуждено, так как событие преступления не имело места».
Здесь пропущена большая посылка — условное суждение «Если событие преступления не имело места, то уголовное дело не может быть возбуждено». Она содержит известное положение Уголовно-процессуального кодекса, которое подразумевается.
Разделительно-категорический силлогизм с пропущенной большей посылкой: «По данному делу не может быть вынесен оправдательный приговор, он должен быть обвинительным».
Большая посылка — разделительное суждение «По данному делу может быть вынесен либо оправдательный, либо обвинительный приговор» не формулируется.
Разделительно-категорический силлогизм с пропущенным заключением:«Смерть произошла либо в результате убийства, либо в результате самоубийства, либо в результате несчастного случая, либо в силу естественных причин. Смерть произошла в результате несчастного случая».
Заключение, отрицающее все другие альтернативы, обычно не формулируется.
23. Условно-категорическим называется умозаключение, одна из посылок которого является условным суждением, а другая посылка и вывод — категорическими суждениями.
Условное суждение имеет форму: если A есть B, то C есть D, например: если Земля вращается вокруг своей оси, то происходит смена дня и ночи. Первое суждение есть основание (антецедент), а второе — следствие (консеквент).
Существуют два модуса условно-категорических умозаключений. Первый из них называется modus ponens, то есть устанавливающий, утверждающий, конструктивный модус; второй называется modus tolens, то есть разрушающий, отрицающий, деструктивный модус.
Конструктивный модус имеет следующий вид.
Если A есть B, то C есть D;
A есть B;
Следовательно, C есть D.
Например:
Если Земля вращается вокруг Солнца, то происходит смена дня и ночи;
Земля вращается вокруг Солнца;
Следовательно, происходит смена дня и ночи.
В условно-категорическом умозаключении в конструктивном модусе утверждается антецедент.
Это правило связано с тем, что при несовместимых суждениях-антецедентах, одно из которых ложно, возможно истинное заключение: если Земля вращается вокруг Солнца, то происходит смена дня и ночи, если Солнце вращается вокруг Земли, то происходит смена дня и ночи, поэтому нельзя сделать заключение: *происходит смена дня и ночи, следовательно, Земля вращается вокруг Солнца.
Деструктивный модус имеет следующий вид.
Если A есть B, то C есть D;
C не есть D;
Следовательно, A не есть B.
В условно-категорическом умозаключении в деструктивном модусе отрицается консеквент.
При отрицании следствия любой из возможных в принципе альтернативных антецедентов окажется ложным: если смены дня и ночи не происходит, то Земля не вращается вокруг Солнца и Солнце не вращается вокруг Земли.
Если человек есть мера всех вещей, то принципы нравственности условны;
Принципы нравственности не условны;
Следовательно, человек не есть мера всех вещей.
Рассмотрим, однако, следующие умозаключения, которые иногда подводят преподавателя:
Если студент слушает лекции, то он приобретает необходимые познания;
Студент N слушал лекции;
Следовательно, он приобрел необходимые познания.
Или:
Если студент слушает лекции, то он приобретает необходимые познания;
Студент N не приобрел необходимых познаний;
Следовательно, он не слушал лекции.
Понятно, что оба они могут оказаться ложными, ибо не всякий, кто слушает лекции, понимает их.
Условием истинности условно-категорического умозаключения является наличие в качестве посылок так называемых невыделяющих суждений, удовлетворяющих условию если и только если.
Итак, доказательным (при условии истинности большей посылки) будет следующее рассуждение:
Если и только если студент слушает лекции, он приобретает необходимые познания;
Студент N не приобрел необходимых познаний;
Следовательно, он не слушал лекций.
24. Разделительно-категорическим называется умозаключение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.
Простые суждения, из которых состоит разделительное (дизъюнктивное) суждение, называются членами дизъюнкции, или дизъюнктами. Например, разделительное суждение «Облигации могут быть предъявительскими или именными» состоит из двух суждений — дизъюнктов: «Облигации могут быть предъявительскими» и «Облигации могут быть именными», соединенных логическим союзом «или».
Утверждая один член дизъюнкции, мы с необходимостью должны отрицать другой и, отрицая один из них, — утверждать другой. В соответствии с этим различают два модуса разделительно-категорического умозаключения: (1) утверждающе-отрицающий и (2) отри-цающе-утверждающий.
1. В утверждающе-отрицающем модусе ( modus ponendo tollens ) меньшая посылка — категорическое суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает другой ее член. Например;
Облигации могут быть предъявительскими (р) или именными (q) Данная облигация предъявительская (q)
Данная облигация не является именной (не-q) Схема утверждающе-отрицающего модуса:
P ^ q > P
1 q '
? — символ строгой дизъюнкции.
Заключение по этому модусу всегда достоверно, если соблюдает-1 ся правило: большая посылка должна быть исключающе-раздели-тельным суждением, или суждением строгой дизъюнкции.Если это правило не соблюдается, достоверного заключения получить нельзя. В самом деле, из посылок «Кражу совершил К. или Л.» и «Кража совершена К.» заключение «Л. кражу не совершал» с необходимостью не следует. Возможно, что Л. также причастен к совершению кражи, является соучастником К.
2. В отрицающе-утверждающем модусе ( modus tollendo ponens ) меньшая посылка отрицает один дизъюнкт, заключение утверждает другой. Например:
Облигации могут быть предъявительскими (р) или именными ( q ) Данная облигация не является предъявительской (не-р)
Данная облигация именная (q)
Схема отрицающе-утверждающего модуса:
< pvq >,1 p
q
< > — символ закрытой дизъюнкции.
Утвердительный вывод получен посредством отрицания: отрицая один дизъюнкт, мы утверждаем другой.
Заключение по этому модусу всегда достоверно, если соблюдается правило: в большей посылке должны быть перечислены все возможные суждения — дизъюнкты, иначе говоря, большая посылка должна быть полным (закрытым) дизъюнктивным высказыванием. Применяя неполное (открытое) дизъюнктивное высказывание, достоверного заключения получить нельзя. Например:
Сделка может быть двусторонней или многосторонней Совершенная сделка не является двусторонней
Совершенная сделка является многосторонней \
Однако это заключение может оказаться ложным, так как в большей посылке учтены не все возможные виды сделок: посылка представляет собой неполное, или открытое, дизъюнктивное высказывание (сделка может быть и односторонней, для совершения которой достаточно изъявления воли одного лица — выдача доверенности, составление завещания, отказ от наследства и т.п.).
Разделительная посылка может включать не два, а три и больше членов дизъюнкции. Например, в процессе расследования причин пожара на складе следователь предположил, что пожар мог возникнуть либо вследствие неосторожного обращения с огнем (р), либо в результате самовоспламенения хранящихся на складе материалов (q), либо в результате поджога (г). В ходе расследования было установлено, что пожар возник вследствие неосторожного обращения с огнем (р). В этом случае все другие дизъюнкты отрицаются. Умозаключение принимает форму утверждающе-отрицающего модуса и строится по схеме:
р ? q ? г, р
1 q л1г
Возможен и другой ход рассуждения. Допустим, предположения о том, что пожар возник вследствие неосторожного обращения с огнем или в результате самовоспламенения хранящихся на складе материалов не подтвердилось. В этом случае умозаключение примет форму отрицающе-утверждающего модуса и будет построено по схеме:
_______ < pvqvr >,1 pv 1 q
г (пожар возник в резульгате поджога)
Заключение будет истинным, если в условной посылке учтены все возможные случаи.
Разделительно-категорическое умозаключение находит широкое применение в судебно-следственной практике, особенно при построении и проверке следственных версий (гл. XI).
25. Умозаключение, в котором одна посылка условное, а другая — разделительное суждения, называется условно-разделительным, или лемматическим 1 .
Разделительное суждение может содержать две, три и большее число альтернатив 2 , поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтернативы) и т.д.
Рассмотрим на примере дилеммы структуру и виды условно-разделительного умозаключения. Различают два вида дилемм: конструктивную (созидательную) и деструктивную (разрушительную), каждая из которых делится на простую и сложную.
В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же следствие. Разделительная посылка утверждает оба возможных основания, заключение утверждает следствие. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствия.
Схема простой конструктивной дилеммы:
Пример: Если обвиняемый виновен в заведомо незаконном задержании (р), то он подлежит уголовной ответственности за преступление против правосудия (г), если он виновен в заведомо незаконном заключении под
От латинского lemma — «предположение».
От латинского alternare — «чередоваться»; каждая из двух или нескольких исключающих друг друга возможностей.
Пример: стражу ( q ), то он также подлежит уголовной отвечст вечности за преступление против правосудия (г)
Обвиняемый виновен или в заведомо незаконном задержании (р), или в заведомо незаконном заключении под стражу (q)
Обвиняемый подлежит уголовной ответственности за преступление против правосудия (г)
В сложной конструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных основания. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствий.
Схема сложной конструктивной дилеммы:
( p -> q ) A ( r -> s ), pvr • q v s
Если сберегательным сертификат является предъявительским (р), то он передается другому лицу путем вручения (q), если он является именным (г), то передается в порядке, установленном для уступки требований (s) Но сберегательный сертификат может быть предъявительским (р) или именным (г)
Сберегательный сертификат передается другому лицу путем вручения (q) или в порядке, установленном для уступки требований (s)
В простой деструктивной дилемме условная посылка содержит одно основание, из которого вытекает два возможных следствия. Разделительная посылка отрицает оба следствия, заключение отрицает основание. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности основания.
Схема простой деструктивной дилеммы:
( p -> q ) A ( p -> r ),1 qv 1 r
Пример: Если Н. совершил умышленное преступление (р), значит, в его деист- ) виях был прямой (q) или косвенный умысел (г). Но в действиях Н. не i было ни прямого (q), ни косвенного умысла (г).
Преступление, совершенное Н., не является умышленным (р)
В сложной деструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.
Схема сложной деструктивной дилеммы:
( p -> q ) A ( r -» s ),1 qv 1 s
1 pv 1 r
Пример: Если предприятие является арендным (р), то оно осуществляет пред^ принимательскую деятельность на основе взятого им в аренду имущественного комплекса (q); если оно является коллективным (г), то осуществляв такую деятельность на основе находящегося в его собственности имущества (s)
Данное предприятие не осуществляет свою деятельность ни на основе взятого в аренду имущественного комплекса (не-q), ни на основе находящегося в его собственности имущества (не-s)
Данное предприятие не арендное (не-р) или не коллективное (не-г)
26. Логический переход от знания об отдельных явлениях к знанию общему совершается в форме индуктивного умозаключения, или индукции (от лат. – наведение).
Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом.
Различают индукцию полную, если посылки исчерпывают весь класс предметов, подлежащих индуктивному обобщению, и неполную, если посылки не исчерпывают всего класса предметов, подлежащих индуктивному обобщению. Выводом как по полной, так и неполной индукции является общее суждение. Полная индукция. Ход мысли осуществляется здесь по схеме: S1 есть Р S2 есть Р …………. Sn есть Р Известно, что S1 , S2 … Sn исчерпывают все предметы класса . Следовательно, все S есть Р. Например:
|
Старший сын в семье Ивановых, Петя, ходит в школу. |
|
Средний сын в семье Ивановых, Кирилл, ходит в школу. |
|
Их младшая сестра Катя ходит в школу. |
|
Петя, Кирилл и Катя – дети в семье Ивановых. |
|
Следовательно, все дети семьи Ивановых посещают школу. |
Из этого примера видно, что общий вывод основан на знании всей совокупности предметов изучаемого класса (мы говорим о всех детях семьи Ивановых) и общий вывод представляет собой категорическое суждение, где предикат посылок и вывода (ходят в школу) один и тот же, как и вообще во всех индуктивных умозаключениях. Но полная индукция не дает знания о других предметах, кроме тех, которые берутся в качестве частных посылок. Эти предметы она характеризует со стороны их родовой принадлежность, и в этом следует усматривать новизну знания, которое индукция порождает. Не будем упускать из вида, что именно знание такого рода лежит в основе дедукции. Однако в реальном человеческом познании индукция занимает незначительное место, так как с полным набором случаев человек в силу ограниченности своего бытия в пространстве и времени, как правило, дела не имеет. Поэтому человеческое мышление обращается кнеполной индукции, в которой общий вывод делают на основании знания не о всех предметах класса, а о некоторой части их. Основанием для переноса знаний от части предметов на весь класс их служит внутренняя природа самих вещей и общественно-историческая практика. Обнаружив сходство либо различие и установив что-либо относительно частных, принадлежащих части класса случаев, человек затем это сходство (различие) переносит на весь класс. Так поступают и в «житейских» ситуациях, и в науке. Многократная практика подтверждает этот перенос и поэтому индукция позволяет сделать более или менее правильный вывод. При этом непременным условием неполной индукции (как и всех индуктивных заключений) является отсутствие противоречивых случаев. Примером неполной индукции через простое перечисление при отсутствии противоречивых случаев может служить следующий ход мысли:
|
Железо – твердое тело; |
|
Медь – твердое тело; |
|
Золото – твердое тело; |
|
Платина – твердое тело. |
|
Следовательно, все металлы – твердые тела. |
Легко видеть, что схема, по которой осуществляется вывод по неполной индукции, такова:
|
S1 есть Р |
|
S2 есть Р |
|
…………. |
|
Sn есть Р |
|
S1, S2 …, Sn – часть класса S |
|
Следовательно, все S есть Р. |
Поскольку вывод по неполной индукции есть скачек, переход от известного к неизвестному и поскольку неполной индукцией сознательно вводится принцип рассмотрения не всего количества предметов, а лишь части из них, постольку выводы по неполной индукции всегда носят вероятностный характер. В силу этого опасность заблуждения при индуктивном умозаключении больше, чем в силлогизме. Если в силлогизме истинность вывода зависит от истинности посылок и соблюдения определенных правил вывода, что само по себе является внешним условием по отношению к самому силлогизму, то в неполной индукции сам скачек несет в себе возможность ошибки, ибо достаточно одного противоречивого случая, чтобы все здание индуктивного умозаключения рухнуло. Например, все учебники логики описывают ситуацию с лебедями на основании неполной индукции; вывод “Все лебеди белые” был опровергнут, когда в Австралии впервые были обнаружены черные лебеди. Или, в нашем предыдущем примере с металлами, мы обнаруживаем, что ртуть (металл) не есть твердое тело, поэтому сделанный вывод оказывается ложным. Каковы же те условия, которые повышают вероятность выводов по неполной индукции?
необходимо брать возможно большее количество случаев для индуктивного обобщения. Например, когда более вероятен вывод о том, что существует внеземная жизнь? В случае, если изучена одна планета солнечной системы или если изучены несколько планет солнечной системы? Последний случай, очевидно, предпочтительней;
вывод будет более вероятен, когда факты, служащие основанием обобщения, более разнообразны и по возможности более полно характеризуют предмет индуктивного обобщения. Это относится и к предыдущему примеру;
вероятность вывода повышается, если предметы, знания о которых индуктивно обобщаются, обладают внутренней объективной связью между собой и чем более существенный признак берется в качестве основы для обобщения.
Для того, чтобы повысить качество выводов по неполной индукции, следует избегать следующих ошибок: 1) «поспешное обобщение». Оно происходит, если в посылках не учтены все обстоятельства, которые, возможно, и являются причиной исследуемого явления. В определенной степени это можно отнести к предсказаниям скорого наступления эры «машинного мышления», которое (предсказание) очевидно основано на поверхностном обобщении работы мозга и ЭВМ; 2) следует избегать ошибки, называемой «после этого, значит, по причине этого» (post hoc, ergo propter hoc); об этом говорилось выше. Научная индукция отличается от неполной индукции через простое перечисление при отсутствии противоречащего случая (такую индукцию называют популярной, так как посылки в ней нередко берутся случайно) тем, что она нацелена на отыскание причинных связей, открытие законов. Поэтому научная индукция основывается на таких методах познания, как наблюдение и эксперимент. О них мы вели речь в лекции по философии.
27. Особую группу индуктивных умозаключений составляют рассуждения, с помощью которых обычно выявляются причинные связи.
Причинность — это определённое внутреннее отношение между явлениями, такая их связь, при которой всякий раз за одним следует другое. Причина — это явление, вызывающее к жизни другое явление. Результат действия причины — следствие.
ЕДИНСТВЕННОЕ СХОДСТВО
Мы привыкли думать, что выявить причинные связи можно путём наблюдения. Однако это не так. Причину можно установить только на основе рассуждения. В логике разработаны определённые методы проведения таких рассуждений, получившие название принципов , или канонов, индукции ( от латинского слова canon , имеющего значения: тростниковый прут, затем прут вообще, далее — линия, обозначающая направление, наконец, — требование, правило).
Первая формулировка этих принципов была дана ещё в начале XVII в. философом Ф. Бэконом. Систематически они были исследованы в прошлом веке философом и логиком Д.-С. Миллем. Отсюда их наименование — «Каноны (принципы) Бэкона-Милля».
Все принципы индукции опираются на рассмотренные выше свойства причинной связи. Каждое явление имеет причину, именно поэтому поиски её не лишены смысла. Причиной может быть только явление, имевшее место до наступления того явления, причину которого мы ищем. После явления, считаемого причиной, всегда должно наступать её следствие. При отсутствии причины следствие не должно иметь места. Изменения в причине влекут за собой изменения в следствии.
Всего принципов, помогающих выявлять причинные связи, пять. (Любопытно, что Милль, перечисливший их, случайно написал в заголовке соответствующей главы: «О четырех методах опытного исследования»).
Принцип единственного сходства: если какое-то обстоятельство постоянно предшествует наступлению исследуемого явления, в то время как иные обстоятельства изменяются, то это обстоятельство есть, вероятно, причина данного явления.
Допустим, мы ищем причину плохого роста посеянных растений (обозначим это явление буквой X). Прежде всего составим перечень всех тех явлений, которые способны, как мы предполагаем, оказаться такой причиной. Наше подозрение может, в частности, упасть на вредителей растений (обозначим этот фактор буквой A ), на высокую температуру (В) , недостаточную влажность ©, неблагоприятный химический состав почвы (D) , плохую её вспашку (Е).
Теперь исследуем несколько полей, на которых посеяны эти растения, и составим сводную таблицу:
1. В условиях А, В, С, D , но не Е имеет место X.
2. В условиях А, В, С, Е , но не D имеет место X.
3. В условиях А, С, D, Е , но не В имеет место X.
4. В условиях B, С, D, Е , но не А имеет место X.
Значит, по всей вероятности, С есть причина X.
Таблица показывает, что всем случаям наличия X сопутствует только фактор С. Иными словами, все ситуации, в которых посеянные растения развиваются плохо, сходны в одном-единственном свойстве: недостаточной влажности. Из этого мы заключаем, что причиной плохого роста растений является, вероятно, именно недостаточная влажность.
ЕДИНСТВЕННОЕ РАЗЛИЧИЕ
Самым надёжным и важным из всех принципов индукции является, пожалуй, принцип единственного различия. Он говорит: если какое-то обстоятельство имеет место, когда наступает исследуемое явление, и отсутствует, когда этого явления нет, а все другое остаётся неизменным, то данное обстоятельство и представляет собой вероятную причину явления.
Общая схема этого принципа:
1. В условиях А, В, С, D имеет место X.
2. В условиях А, В, D , но не С отсутствует X.
Вероятно, что С есть причина X.
Например, в нормальном воздухе свеча горит, а в воздухе, лишённом кислорода, гаснет. Из этого можно заключить, что кислород — необходимая предпосылка горения.
На поле, которое было хорошо удобрено, хлеба буйно пошли в рост. На соседнем, в общем точно таком же поле удобрения не применялись и посевы развивались плохо. Единственное различие этих полей — удобрения — и является, скорее всего, причиной хорошего роста растений.
Сад, где выращивались груши сорта «вильямсия», буйно цвёл, но не плодоносил, хотя климатические условия были благоприятными. Возник вопрос, отчего это. Было замечено, что плодоносили только те деревья «вильямсии», возле которых росли случайно сохранившиеся экземпляры груш сорта «фаворитка». Из этого был сделан вывод, что соседство с «фавориткой» находится в причинной связи с плодоношением «вильямсии». Этот вывод оказался правильным. Последующее изучение выявило тот факт, что груши сорта «вильямсия» плодоносят только после опыления их цветов пыльцой другого сорта.
СХОДСТВО И РАЗЛИЧИЕ
Принципы единственного сходства и единственного различия, применённые вместе, дают объединённый принцип сходства и различия: если два или большее число случаев, когда наступает данное явление, сходны только в одном обстоятельстве, в то время как два или больше случаев, когда этого явления нет, различаются только тем, что данное обстоятельство отсутствует, то это обстоятельство и есть, вероятно, причина рассматриваемого явления.
СОПУТСТВУЮЩИЕ ИЗМЕНЕНИЯ
Если с изменением одного явления изменяется и другое, а остальные обстоятельства остаются неизменными, то между данными явлениями существует, по всей вероятности, причинная связь.
Это принцип сопутствующих изменений.
Схематично:
1. В условиях А, В, С имеет место X.
2. В условиях изменения А и постоянства В и С имеет место изменение X.
Следовательно, А есть, вероятно, причина X.
Например, если по мере увеличения температуры газа увеличивается его объём, то можно сделать вывод, что между температурой и объёмом имеется причинная связь.
Этот принцип широко применим в тех случаях, когда какую-то характеристику нельзя, подобно температуре, полностью исключить, но можно в определённых пределах варьировать.
ОСТАЮЩАЯСЯ ЧАСТЬ ПРИЧИНЫ
Если сложная причина производит сложный результат и известно, что часть причины вызывает определённую часть этого результата, то остающаяся часть причины производит, по всей вероятности, остальную часть результата. Это принцип остатков.
Схематично:
1. Сложное явление АВ есть причина сложного следствия XY.
2. В есть причина Y .
Значит, А — вероятная причина X.
К примеру, взвешивалась доза вещества определённого химического состава. Оказалось, что общий вес этой дозы несколько больше, чем вес составных частей вещества, предполагаемых формулой. Избыток веса говорил о наличии примеси. Так был открыт химический элемент литий.
28. В науке и практических делах объектом исследования нередко выступают единичные, неповторимые по своим индивидуальным характеристикам события, предметы и явления. При их объяснении и оценке затруднено применение как дедуктивных, так и индуктивных рассуждений. В этом случае прибегают к третьему способу рассуждения —умозаключению по аналогии: уподобляют новое единичное явление другому, известному и сходному с ним единичному явлению и распространяют на первое ранее полученную информацию.
Например в истории физики, когда при выяснении механизма распространения звука его уподобили движению жидкости. На основе этого уподобления возникла волновая теория звука. Объектами уподобления в этом случае были жидкость и звук, а переносимым признаком — волновой способ их распространения.
Умозаключение по аналогии — это вывод о принадлежности определенного признака исследуемому единичному объекту (предмету, событию, отношению или классу) на основе его сходства в существенных чертах с другим уже известным единичным объектом.
Умозаключению по аналогии всегда предшествует операция сравнения двух объектов, которая позволяет установить сходства и различия между ними. При этом для аналогии требуются не любые совпадения, а сходства всущественных признаках при несущественности различий. Именно такие сходства служат основой кля уподобления двух материальных или идеальных объектов.
Логический переход от известного к новому знанию регулируется в выводах по аналогии следующим правилом: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других, обнаруженных в одном из сравниваемых предметов, признаках.
