2. Определение неизвестных параметров распределения.

   C помощью гистограммы мы можем приближенно построить график плотности распределения случайной величины . Вид этого графика часто позволяет высказать предположение о плотности распределения вероятностей  случайной величины . В выражение этой плотности распределения обычно входят некоторые параметры, которые требуется определить из опытных данных.     Остановимся на том частном случае, когда плотность распределения  зависит от двух параметров.     Итак, пусть x₁, x₂, ..., x_n - наблюдаемые значения непрерывной случайной величины , и пусть ее плотность распределения вероятностей зависит от двух неизвестных параметров A и B, т.е. имеет вид . Один из методов нахождения неизвестных параметров A и B состоит в том, что их выбирают таким образом, чтобы математическое ожидание и дисперсия теоретического распределения совпали с выборочными средними значением  и дисперсией :

(66)

где

(67)

Из двух полученных уравнений (66) находят неизвестные параметры A и B. Так, например, если случайная величина  подчиняется нормальному закону распределения вероятностей, то ее плотность распределения вероятностей

зависит от двух параметров a и . Эти параметры, как мы знаем, являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины ; поэтому равенства (66) запишутся так:

(68)

Следовательно, плотность распределения вероятностей имеет вид

Замечание 1. Такую задачу мы уже решали в § 7. Результат замера есть случайная величина , подчиняющаяся нормальному закону распределения с параметрами a и . За приближенное значение a мы выбрали величину , а за приближенное значение  - величину .

Замечание 2. При большом количестве опытов нахождение величин  и  по формулам (67) cвязано с громоздкими вычислениями. Поэтому поступают так: каждое из наблюдаемых значений величины , попавшее в i-й интервал ] X_i-1, X_i [ статистического ряда, считают приближенно равным середине c_i этого интервала, т.е. c_i=(X_i-1+X_i)/2. Рассмотрим первый интервал ] X₀, X₁ [. В него попало m₁наблюдаемых значений случайной величины , каждое из которых мы заменяем числом с₁. Следовательно, сумма этих значений приближенно равна m₁с₁. Аналогично, сумма значений , попавших во второй интервал, приближенно равна m₂с₂ и т.д. Поэтому

Подобным же образом получим приближенное равенство

Итак,

(69)

где n=m₁+m₂+...+m_k, а k - число интервалов статистического ряда.

Замечание 3. На практике для еще большего упрощения вычислений прибегают к следующему приему. Пусть x₀ - произвольное число. Обозначим u_i=с_i-x₀ и рассмотрим величины v₁ и v₂, определяемые соотношениями

(70)

Покажем, что

(71)

Действительно,

так как

[cм.формулы (69)].

Итак, , откуда . Аналогично доказывается и второе из соотношений (71)

 Пример. Построенная гистограмма для статистического распределения значений диаметра вала хвостовика (см. рис. 17) позволяет сделать предположение о том, что мы имеем дело с нормальным законом распределения. Требуется, исходя из опытных данных, представленных в таблице из примера п.8.1., определить параметры a и  этого распределения.

   Решение. Полагая* x₀=75, вычислим v₁ и v₂. Вычисления расположим, как указано в следующей таблице.

Номера интервалов	Cередина интервала ci	mi	ui=сi-75	miui
1	67	4	-8	-32	64	256
2	69	12	-6	-72	36	432
3	71	24	-4	-96	16	384
4	73	41	-2	-82	4	164
5	75	50	0	0	0	0
6	77	53	2	106	4	212
7	79	39	4	156	16	624
8	81	26	6	156	36	936
9	83	13	8	104	64	832
10	85	5	10	50	100	500
11	87	2	12	24	144	288
12	89	1	14	14	196	196
		270		328		4824

По формулам (70) находим

Используя теперь формулы (71), имеем

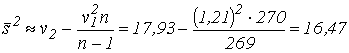
   Выберем параметры a и  так, чтобы выполнялись условия (68): , . Следовательно, . Таким образом, плотность распределения вероятностей

   В следующей таблице приведены вычисления значений функции  в средних точках интервала статистического ряда. Значения функции  взяты из Табл. I Приложения.

x	x-76,21
67	-9,21	-2,27	0,0303	0,006	0,008
69	-7,21	-1,78	0,0818	0,020	0,022
71	-5,21	-1,29	0,1736	0,043	0,045
73	-3,21	-0,79	0,2920	0,072	0,076
75	-1,21	-0,30	0,3697	0,091	0,092
77	0,79	0,20	0,3825	0,095	0,098
79	2,79	0,69	0,3144	0,075	0,072
81	4,79	1,18	0,1989	0,049	0,048
83	6,79	1,62	0,0973	0,024	0,024
85	8,79	2,17	0,0379	0,009	0,009
87	10,79	2,66	0,0116	0,003	0,004
89	12,79	3,16	0,0020	0,001	0,002

   В последнем столбце таблицы приведены значения функции , взятые из столбца (5) таблицы из примера из п.8.1. Сравнение показывает, что функция  близка к .

* Для простоты вычислений, как это обычно делается, за x₀ мы выбрали число, близкое к середине диапазона изменения наблюдаемых значений.