
Медведева Основы теории множеств и теории отображений 2011
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ "МИФИ"
М.В. Медведева
Основы теории множеств и теории отображений
Рекомендовано УМО "Ядерные физика и технологии" в качестве учебного пособия для студентов высших учебных заведений
Москва 2011
УДК 517.982(075) ББК 22.162я7 М42
Медведева М.В. Основы теории множеств и теории отображений. Учебное пособие. М.: НИЯУ МИФИ, 2011. – 52 с.
Подробно изложены основы теории множеств и теории функций, начиная с простых понятий и последовательно усложняя их структуру. Большая часть излагаемой здесь теории читается для определенных пространств в различных курсах лекций МИФИ, таких как ”Теория функций действительных переменных”, ”Теория функций комплексного переменного”, ”Теория дифференциальных уравнений”, ”Теория интегральных уравнений”.
В написании первых двух глав принимала участие Н.А. Дружинина, преподаватель математики ГОУ СОШ № 550 г. Москвы.
Пособие предназначено для студентов МИФИ.
Подготовлено в рамках Программы создания и развития НИЯУ МИФИ.
Рецензент проф., д-р физ.-мат. наук Н.А. Кудряшов ISBN 978-5-7262-1465-8
c Национальный исследовательский ядерный университет ”МИФИ”, 2011
ОГЛАВЛЕНИЕ
Глава 1. Элементы теории множеств ............................................ |
4 |
Глава 2. Функции (отображения) .................................................. |
9 |
Глава 3. Метрические пространства .............................................. |
13 |
Глава 4. Последовательности. Отображения метрических |
|
пространств ................................................................................ |
19 |
Глава 5. Полные метрические пространства ................................. |
23 |
Глава 6. Компактные метрические пространства ......................... |
28 |
Глава 7. Нормированные пространства ......................................... |
34 |
Глава 8. Евклидовы и унитарные пространства ........................... |
46 |
Список рекомендуемой литературы ............................................. |
52 |
3
ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Если A – произвольное множество элементов, то утверждение "элемент a принадлежит множеству A" принято записывать так: a 2 A. Если элемент a не принадлежит множеству A, то записывают a 62A. Если все элементы множества A принадлежат и множеству B, то говорят, что A является подмножеством множества B, и пишут A B. Если все элементы множества A принадлежат множеству B и все элементы множества B принадлежат множеству A, то говорят, что множества A и B равны, и пишут A=B. Итак, A=B тогда и только тогда, когда A B и B A. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ;. Пустое множество является подмножеством любого множества A.
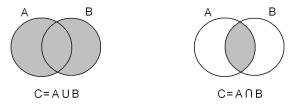
Определение 1.1. Объединением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B. Записывают C = A [ B.
Замечание. Если x 2 A[B, то часто говорят: "элемент x принадлежит множеству A или множеству B". При этом в данном выражении допускается, что x принадлежит и множеству A и множеству B.
Определение 1.2. Пересечением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих как множеству A, так и множеству B. Записывают C = A \ B.
Если пересечение множеств A и B пустое, то есть A \ B = ;, тогда говорят, что множества A и B не пересекаются.
Рис. 1.1 |
Рис. 1.2 |
Из этих определений непосредственно следует, что операции объединения и пересечения множеств коммутативны и ассоциативны, то есть
A [ B = B [ A;
A \ B = B \ A;
(A [ B) [ C = A [ (B [ C);
4
(A \ B) \ C = A \ (B \ C):
Докажем не столь очевидные свойства этих операций.
Утверждение 1.1. Для любых множеств A и B выполняются
равенства |
|
(A [ B) \ C = (A \ C) [ (B \ C); |
(1) |
(A \ B) [ C = (A [ C) \ (B [ C): |
(2) |
Доказательство. Докажем равенство (1). Если x 2 (A [ B) \ C, то по определению пересечения двух множеств получим x 2 (A [ B) и x 2 C. Отсюда следует, что элемент x принадлежит хотя бы одному из множеств A или B и при этом x принадлежит множеству C. Поэтому x принадлежит хотя бы одному из множеств A \C или B \C. Отсюда следует x 2 (A\C)[(B\C). Итак, получили, что множество (A[B)\C является подмножеством множества (A \ C) [ (B \ C).
Пусть теперь x 2 (A \ C) [ (B \ C). Это означает, что элемент x принадлежит хотя бы одному из множеств A \ C или B \ C. Следовательно, x принадлежит множеству C и при этом x 2 A или x 2 B. Значит, x 2 C и x 2 A [ B, то есть x 2 (A [ B) \ C. Итак, теперь получили, что множество (A \ C) [ (B \ C) является подмножеством множества (A [ B) \ C. Тогда (A \ C) [ (B \ C) = (A [ B) \ C.
Докажем равенство (2). Если x 2 (A \ B) [ C, то по определению объединения двух множеств получим x 2 A \ B или x 2 C. Отсюда следует, что или элемент x принадлежит и множеству A и множеству B, или x принадлежит множеству C. Поэтому x принадлежит хотя бы одному из множеств A или C и при этом принадлежит хотя бы одному из множеств B или C , то есть x 2 A [ C и x 2 B [ C. Значит, x 2 (A [ C) \ (B [ C). Итак, получили, что множество (A \ B) [ C является подмножеством множества (A [ C) \ (B [ C).
Пусть теперь x 2 (A [ C) \ (B [ C). Это означает, что элемент x принадлежит и множеству A [ C и множеству B [ C. Следовательно, x принадлежит или множеству C или множеству A и при этом принадлежит или множеству C или множеству B. Если x – элемент множества C, то по определению объединения двух множеств получим, что x 2 (A \B) [C. Если же x не является элементом множества C, то тогда x принадлежит множеству A и при этом множеству B, то есть x 2 A \ B, а значит, x 2 (A \ B) [ C. Итак, теперь получили, что множество (A [ C) \ (B [ C) является подмножеством множества
(A \ B) [ C. Поэтому (A [ C) \ (B [ C) = (A \ B) [ C. Утверждение доказано.
5
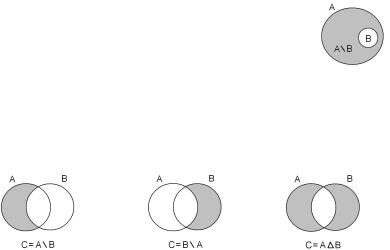
Определение 1.3. Разностью множеств A и B называется множество C, состоящее из всех элементов множества A, не принадлежащих множеству B. Записывают C = AnB.
Разность множеств AnB, вообще говоря, не совпадает с разностью BnA. Например, для A = [0; 2] и B = [1; 3] множество AnB = [0; 1), а BnA = (2; 3], и потому AnB 6= BnA.
Определение 1.4. Если B является подмножеством A, то разность AnB называется дополнением множества B до множества A или просто дополнением множества B.
Заметим, что если B A, то A = (AnB) [ B.
Рис. 1.3
Определение 1.5. Симметрической разностью двух множеств A и B называется объединение множеств AnB и BnA. Записывают
A4B = (AnB) [ (BnA).
Рис. 1.4 |
Рис. 1.5 |
Рис. 1.6 |
Утверждение 1.2. Для любых множеств A и B выполняется равенство A4B = (A[B)n(A\B), то есть множество A4B является дополнением множества A \ B до множества A [ B.
Доказательство. Пусть x 2 A4B. Если при этом x 2 AnB, то получим x 2 A, x 62B. Из определений объединения и пересечения множеств следует, что тогда x 2 A [ B, x 62A \ B. Поэтому x 2 (A [ B)n(A \ B). Если же x 62AnB, то тогда x 2 BnA, так как x 2 A4B = = (AnB) [ (BnA). Значит, x 2 B, x 62A. Отсюда получим x 2 A [ B, x 62A \ B, то есть x 2 (A [ B)n(A \ B). Это означает, что множество A4B является подмножеством (A [ B)n(A \ B).
Пусть теперь x 2 (A [ B)n(A \ B). Тогда x 2 A [ B, x 62A \ B. Если при этом x 2 A, то тогда x 62B (иначе x 2 A \ B), а значит, x 2 AnB. Если же x 62A, то тогда x 2 B, так как x 2 A [ B.
6

И, значит, x 2 BnA. Получили, что x 2 AnB или x 2 BnA, то есть x 2 (AnB)[(BnA) = A4B. Это означает, что множество (A[B)n(A\B) является подмножеством A4B.
Поэтому A4B = (A [ B)n(A \ B). Утверждение доказано.
Аналогично понятиям объединения и пересечения двух множеств определяются понятия объединения и пересечния любого (конечного или бесконечного) числа множеств. Если задано множество M и каждому 2 M сопоставлено некоторое множество A , то говорят, что
задано семейство множеств fA g, 2 M. |
|
|
|
|
|
|
|
|
|||||||||||
Определение |
|
1.6. Пусть |
задано семейство множеств A , |
||||||||||||||||
2 M. Тогда объединением этих множеств называется множество |
|||||||||||||||||||
C, состоящее из всех элементов, принадлежащих хотя бы одному из |
|||||||||||||||||||
множеств A . Записывают C = |
2M |
A . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определение |
|
1.7. Пусть |
заданоS |
|
семейство множеств A , |
||||||||||||||
2 M. Тогда пересечением этих множеств называется множество |
|||||||||||||||||||
C, состоящее из всех элементов, принадлежащих каждому из мно- |
|||||||||||||||||||
жеств A . Записывают C = |
|
|
T |
A . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2M |
|
|
|
|
|
T |
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
S |
A и |
|
|
|
|
|
|||||||
Иногда пишут немного короче: |
|
A . Для множества нату- |
|||||||||||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
S |
|
|
||
ральных чисел вместо записи |
|
A часто используют запись |
An, |
||||||||||||||||
|
2N |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|||
T |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A – запись |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а вместо записи |
|
An. |
|
|
|
|
|
|
|
|
|
|
|||||||
2N |
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Например, рассмотрим отрезки A1 = [0; 1], A2 = [0; 1 ], A3 |
= [0; |
1 ], |
|||||||||||||||||
|
[0; n1 ], n 2 N. Пересечением |
|
2 |
|
|
|
3 |
||||||||||||
..., то есть An = |
этих отрезков явля- |
||||||||||||||||||
|
|
|
A |
|
1 |
|
|
; |
|
|
|
1 |
[3; + |
|
) |
|
|
|
|
|
|
|
|
T |
|
|
|
|
T |
|
|
|
|
||||||
ется точка 0, при этом пишут n=1 An |
= |
|
n=1[0; n1 ] = |
f0g. Или рас- |
|||||||||||||||
смотрим семейство отрезков |
= |
|
1 |
|
1 |
, |
2 |
1 . Объедине- |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||
нием этих отрезков является |
интервал (0; 1), то есть |
2[3S;+1) |
|
= |
|||||||||||||||
|
|
A |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= S 1 ; 1 = (0; 1).
2[3;+1)
Далее при доказательстве некоторых теорем будет использоваться следующая теорема, которая называется принципом двойственности.
Теорема 1.1 (принцип двойственности). Пусть задано семейство множеств A , 2 M. Тогда для любого множества B выполняется:
7
S |
T |
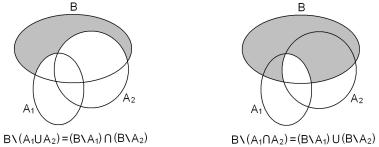
1. Bn A = |
(BnA ) (дополнение объединения равно пересе- |
2M |
2M |
чению дополнений).
T |
S |
2. Bn A = |
(BnA ) (дополнение пересечения равно объеди- |
2M |
2M |
нению дополнений).
Рис. 1.7 |
Рис. 1.8 |
Доказательство. 1. Пусть x 2 Bn |
S |
A . Тогда из определения |
|
|
2M |
S
разности множеств следует, что x 2 B и x 62 A . Значит, x не
2M
принадлежит ни одному из множеств A и при этом принадлежит множеству B, то есть элемент x принадлежит каждому из множеств
BnA . Следовательно, x 2 |
T |
(BnA ). |
|
T |
2M |
Обратно, пусть x 2 |
(BnA ). Тогда для всякого 2 M имеем |
2M |
|
x 2 BnA . Поэтому x 2 B и для всех 2 M выполняется x 62A , то
S |
|
|
S |
|
|
есть x 62 A . Следовательно, x 2 Bn A . |
|
|
|||
2M |
S |
2M |
|
|
|
Это означает, что Bn |
T |
|
|
||
|
A = |
(BnA ). |
|
|
|
T |
2M |
2M |
|
M |
|
B |
|
T |
|||
2. Пусть x 2 Bn |
A . Тогда x 2 B и x 62 |
A . Поэтому x |
|||
2M |
|
|
2M |
2 |
|
принадлежит множеству |
|
, и при этом для некоторого |
элемент |
||
x не принадлежит множеству A . То есть x принадлежит хотя бы
S
одному из множеств BnA . Отсюда следует, что x 2 (BnA ).
2M
8
S
Пусть теперь x 2 (BnA ). Тогда для некоторого 2 M имеем
2M
x 2 BnA . Значит, x 2 B и x 62A для некоторого 2 M, то есть
T |
T |
x 62 A . Поэтому x 2 Bn |
A . |
2M |
2M |
T |
S |
Это означает, что Bn |
A = (BnA ). |
2M |
2M |
Теорема доказана. |
|
В некоторых вопросах используется понятие произведения множеств.
Определение 1.8. Множество всех упорядоченных пар (a; b), где a 2 A, b 2 B, называется произведением множеств A и B и обозначается A B.
То есть A B = f(a; b) : a 2 A; b 2 Bg. Отметим, что A B, вообще говоря, не совпадает со множеством B A.
ГЛАВА 2. ФУНКЦИИ (ОТОБРАЖЕНИЯ)
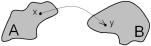
Определение 2.1. Пусть A и B |
|
|
два произвольных множества. Если каж- |
|
|
дому элементу x множества A постав- |
|
|
лен в соответствие некоторый элемент |
|
|
y множества B, то говорят, что задано |
|
|
отображение (функция) множества A в |
Рис. 2.1 |
|
множество B. |
||
|
Пишут f : A ! B, y = f(x).
Элемент y называют образом элемента x. Образом множества X A при отображении f называется множество всех элементов f(x), где x 2 X. Этот образ обозначается f(X). Записывают f(X) = = ff(x) 2 B : x 2 Xg.
Если y 2 B, то множество всех элементов x из A для которых f(x) = y называется прообразом элемента y и обозначается f 1(y), то есть f 1(y) = fx 2 A : f(x) = yg. Аналогично определяется понятие прообраза для всякого множества Y B: прообразом множества Y при отображении f называется множество всех элементов из A, образы которых принадлежат Y , то есть f 1(Y ) = fx 2 A : f(x) 2 Y g. Прообраз множества может оказаться пустым множеством.
9
Пример. Рассмотрим отображение f : R ! R, f(x) = x2. Для
этого отображения |
f(3) = 9 |
, |
f([1; 2]) = [1; 4] |
f 1(9) = |
f |
3; 3 |
g, |
|
, |
|
|
||||
f 1( 2) = ;, f 1([ 3; 2]) = ;, |
f 1([1; 4]) = [ 2; 1] [ [1; 2]. |
|
|
||||
Докажем теперь общие свойства функций. |
|
|
|
|
|||
Теорема 2.1. Пусть задано отображение f : A ! B. Тогда для любых множеств M1 B и M2 B выполняется
f 1(M1 [ M2) = f 1(M1) [ f 1(M2)
(прообраз объединения двух множеств равен объединению их прообразов).
Доказательство. Пусть x 2 f 1(M1 [M2). Тогда f(x) 2 M1 [M2
и, значит, f(x) 2 M1 или f(x) 2 M2. Поэтому x 2 f 1(M1) или x 2 f 1(M2). Следовательно, x 2 f 1(M1) [ f 1(M2).
Если x 2 f 1(M1) [ f 1(M2), то тогда x 2 f 1(M1) или x 2 f 1(M2). Поэтому f(x) 2 M1 или f(x) 2 M2. Следовательно,
f(x) 2 M1 [ M2. Отсюда получим x 2 f 1(M1 [ M2).
Это означает, что f 1(M1 [ M2) = f 1(M1) [ f 1(M2).
Теорема 2.2. Пусть задано отображение f : A ! B. Тогда для любых множеств M1 B и M2 B выполняется
f 1(M1 \ M2) = f 1(M1) \ f 1(M2)
(прообраз пересечения двух множеств равен пересечению их прообразов).
Доказательство. Пусть x 2 f 1(M1 \M2). Тогда f(x) 2 M1 \M2, то есть f(x) 2 M1 и f(x) 2 M2. Значит, x 2 f 1(M1) и x 2 f 1(M2).
Поэтому x 2 f 1(M1) \ f 1(M2). |
x 2 f 1(M1) и |
Пусть теперь x 2 f 1(M1) \ f 1(M2). Тогда |
|
x 2 f 1(M2). Следовательно, f(x) 2 M1 и f(x) |
2 M2. Поэтому |
f(x) 2 M1 \ M2. Значит, x 2 f 1(M1 \ M2). |
|
Отсюда следует, что f 1(M1 \ M2) = f 1(M1) \ f 1(M2).
Теорема 2.3. Пусть задано отображение f : A ! B. Тогда для любых множеств M1 A и M2 A выполняется
f(M1 [ M2) = f(M1) [ f(M2)
(образ объединения двух множеств равен объединению их образов).
Доказательство. Рассмотрим y такой, что y 2 f(M1 [ M2). Найдется x 2 M1 [ M2 для которого f(x) = y. Тогда x 2 M1 или x 2 M2.
10
