Лапшинский Сборник задач и заданий с ответами, решениями 2011

которого надо измерить, всего лишь двумя контактами, как показано на рис. 1.15,а. Обозначения на схеме: Rx – сопротивление участка цепи между контактами (отмечены стрелками), Е – источник эталонного напряжения, А – микроамперметр с очень малым внутренним сопротивлением (Rвн << Rэт), Rэт – эталонный резистор, определяющий величину максимального измеряемого тока (при закороченных контактах). Если Iизм – измеренное значение тока, то очевидно,

что Rx = E/Iизм – Rэт.

Вместо этого был использован четырехконтактный (четырехзондовый) метод, схема которого показана на рис.1.15,б. К отмеченным элементам добавлен вольтметр V с очень большим входным сопротивлением (Rвх >> Rx при любых значениях Rx), который подключен непосредственно к измеряемому участку цепи. Цепь с источником напряжения подключена к внешним контактам.

Рис. 1.15. Схемы измерений сопротивления участка цепи на нанотрубке:

(а) – двухзондовым и (б) – четырехзондовым методом

Можно предположить, что поскольку был использован четырехзондовый метод, то он дает более точные результаты. Определите насколько более точные. Оцените максимальную относительную погрешность (в %) измерения для обоих методов, если при измерении удельного сопротивления

41

различных нанотрубок четырехзондовым методом были получены следующие экспериментальные данные, таблица

1.2.

Таблица 1.2. Экспериментальные данные по измерению удельного сопротивления нанотрубок

Дополнительный вопрос: чем можно объяснить очень большой (6 порядков!) разброс измеренных значений удельного сопротивления для различных образцов нанотрубок? Ваше мнение?

Задача №11. Фотоприемные устройства (ФУ) на квантовых ямах (наногетероструктурах). Определите долю мощности оптического излучения, поглощаемого в фотоприемнике на квантовых ямах. Излучение падает перпендикулярно к поверхности фотоприемника. Коэффициент поглощения излучения в узкозонном полупроводнике α = 7·103 см-1, коэффициенты отражения от

узкозонного полупроводника d = 5нм, число периодов фотоприемной структуры n = 50. Ответ представить в виде аналитического выражения и численного значения. Преобразовать ответ для R1 = R2 = 0. Объяснить полученный результат.

42

Комментарий к задаче №1122 Фрагмент сечения фотоприемника на квантовых ямах

схематично показан на рис.1.16. Заштрихованные области – узкозонный полупроводник. Границы раздела между узкозонным и широкозонным полупроводниками, на которых коэффициенты отражения имеют значения R1 и R2, также показаны на рис. 1.16.

Рис.1.16. Схема фрагмента сечения фотоприемника на квантовых ямах

22 Смотрите сначала комментарий к задачам № 4-6 2009 года

43

Коэффициент отражения R – отношение мощности оптического излучения, отраженного от границы раздела двух сред к мощности падающего излучения. Излучение, поглощаемое в узкозонном полупроводнике, преобразуется в электрический сигнал и только оно является полезным для работы фотоприемника. В широкозонном полупроводнике излучение не поглощается, т.к. в нем нет энергетических уровней или зон, энергия которых соответствует энергии фотона.

Поглощение оптического излучения подчиняется закону Бугера-Ламберта

P(x) = P0e-αx,

где: x – координата в направлении, перпендикулярном поверхности полупроводника, совпадающим с направлением падения излучения, начало координат лежит на поверхности, P(x) – мощность оптического излучения в точке с координатой x, P0 – мощность излучения на поверхности, e – число Эйлера, α – коэффициент поглощения.

Для решения задачи воспользуйтесь справочными данными: скорость света – c ≈ 3·108 м/с; постоянная Планка – h ≈ 6,63·10-34 Дж·с; число Эйлера – e ≈ 2,72.

44

Задача №3. Зарядка Земли одним электроном. Ответы на поставленные вопросы:

1) Для того, чтобы доставить заряд CV на электрод, необходимо преодолеть отталкивающий потенциал электрода, который во время зарядки возрастает от 0 до V со средним значением V/2. Поэтому, энергия, требуемая на зарядку электрода равна:

1Q V CV 2

22

2)Для того, чтобы преодолеть отталкивающий потенциал кусочка металла, который во время зарядки возрастает от 0

ЧАСТЬ Б. Элементы ИМС и ИНС и устройства на их основе

Задача №4. Фотоприемная матрица на основе наногетероструктур. Как сказано в комментариях к задаче, в фотоприемниках на квантовых ямах поглощение фотонов вызывает переход электронов между разрешенными уровнями энергии в квантовой яме. Определим энергию фотона hυ, обеспечивающего переход электрона с уровня Е1 на уровень Е2:

46

hυ = Е2- Е1 = 0,125 эВ.

Определим длину волны λ, соответствующую этой энергии: υ = c/λ, где с – скорость света, следовательно, hc/λ = Е2- Е1, отсюда λ = 9,93 мкм.

Определим разность энергий Е дна зоны проводимости широкозонного и узкозонного полупроводников (рис. 1.6):

Е = (Еg2 – Еg1)/2 = 0,175 эВ.

Отсюда видно, что положение уровня Е2 совпадает с дном зоны проводимости широкозонного полупроводника. Поэтому при попадании на структуру фотонов с энергией, большей Е2 – Е1,они также будут поглощаться и вызывать переходы электронов с уровня Е1 в зону проводимости широкозонного полупроводника. Следовательно, фотоприемник будет работать и при длине волны, меньшей, чем определена выше. Значит, расчетное значение будет: λ < 9,93 мкм.

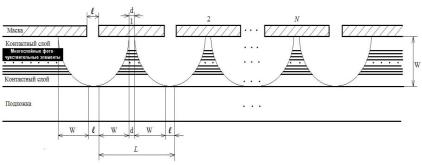
Рис.1.17. Схема сечения фрагмента фотоматрицы

47

Задача №5. Фотоприемная матрица инфракрасного (ИК) диапазона для передачи изображения телевизионного стандарта. Для наглядности решения удобно нарисовать фрагмент сечения фотоматрицы вдоль строки (или столбца) –

рис.1.17

Как видно из рисунка, при изотропном травлении (скорость травления одинакова во всех направлениях) при травлении образца в глубину происходит растравливание вдоль поверхности на такую же величину. Поэтому необходимо определить толщину w слоя, подлежащего травлению:

W = hr + n (he+ hi) + hi = 2670 + 50 (5 + 45) + 45 = 5215 нм.

Оценим минимально допустимый шаг L чувствительных элементов в фотоматрице. Как видно из рисунка:

L = 2w + d + l = 2×5,215 + 1+ 1 = 12,43 мкм.

Определим число элементов в фотоматрице: число строк задано N = 600, соотношение сторон в современном телевизионном стандарте составляет 3:4. Следовательно, при квадратной форме чувствительного элемента число столбцов в матрице М = 800.

Определим требуемую площадь S без учета ширины периферийных участков:

S= (N×L) × (M×L) = 600×800×(12,43)2 = 74162352 мкм2

~74.2 мм2.

Задача №6. Снайпер, вооруженный инфракрасным прицелом. Определим величину фототока Iф, который может «почувствовать» фотоматрица. Это можно сделать, зная

Iф = U·С·f = 10-3·10-12·50 = 5·10-14 А.

Определим мощность P1 излучения, обеспечивающего найденный фототок фотоприемной ячейки, зная ее фоточувствительность:

Iф = P1R = P1αGq/hυ.

Отсюда получаем P1 = Iфhυ/αGq = 1,72·10-14 Вт. При этом считаем энергию фотона для средней длины волны из диапазона фоточувствительности λ = 9 мкм.

Определим плотность мощности излучения Pфп, падающего на фотоприемник. Найденная величина P1 – мощность излучения, падающего на элементарную фотоприемную ячейку. Для нахождения плотности мощности ее необходимо разделить на площадь фотоприемной ячейки:

Рфп = P1/ S1,

S1 = 30·30·10-12 = 9·10-10 м2,

Рфп = 1,9·10-5 Вт/м2.

Определим плотность мощности Pвх оптического излучения на входе оптической системы, зная коэффициент усиления оптической системы:

Pфп = Pвх·Kопт = PвхηоSвх/Sфп,

где: Sвх = πD2/4 = 201 мм2 и Sфп = 75 мм2 – площади входного отверстия объектива и фотоприемной матрицы

соответственно. Отсюда имеем: Pвх = 9,53·10-6 Вт/м2. Определяем плотность мощности излучения солдата про-

тивника Bэ. По таблице 1.1 для температуры тела человека (310 К) в диапазоне длин волн 8-10 мкм находим Bэч = 73,2 Вт/м2. Отсюда следует, что Bэ = КBэч = 0,6·73,2 = 43,92 Вт/м2.

49

противника, записываем соотношение Pвх = ηсBэ S/l2, где S излучающая площадь объекта наблюдения, т.е. площадь лица солдата. Для оценки этой площади можно принять, что она представляет собой круг диаметром 200 мм, тогда S = 0,03 м2. Подставляя найденные величины, определяем расстояние l = 288 м. Поскольку ряд параметров при расчете носят оценочный характер, можно сказать, что искомое расстояние составляет около 300 м.

Задача №7. Одноэлектронный транзистор при комнат-

ной температуре. Изменение энергии при заряде одним

T =300 К емкость конденсатора составляет C =3·10-19 Ф.

Задача №8. Площадь обкладок конденсатора для одноэлектронного транзистора. Ёмкость конденсатора

Для квадратных обкладок конденсатора сторона квадрата составляет 4 нм.

Задача №9. Тепловыделение процессора современного компьютера. Решение выглядит так:

N Cn Vdd2 f 10-8 см-2х10-14хФх12 В2х10-9 с-1 = 100 Вт/см2

50