Исаенкова Лабораторная работа Рентгенографическое 2007

6. МЕТОДЫ РАСЧЕТА МАКРОНАПРЯЖЕНИЙ

6.1. sin2ψ-Метод

Рассмотрим плоский изотропный поликристаллический образец, который находится в плосконапряженном состоянии

где ν − коэффициент Пуассона, E − модуль Юнга, и

Деформация εφψ в направлении, заданном сферическими углами φ и ψ, имеет вид

31

Если экспериментально определены εφψ для нескольких значе-

E

откуда можно определить σ1 и σ2.

6.2. Нелинейность в sin2ψ − методе

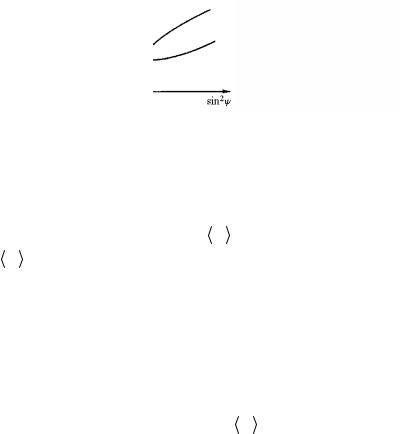
При рентгенографическом определении остаточных напряжений sin2ψ − методом в некоторых материалах, например в рельсовых сталях, наблюдается нелинейный характер в зависимости εφψ = =f(sin2ψ), который нельзя объяснить экспериментальными неточностями (рис. 6.2, а).

Подробный анализ этого явления привел к заключению, что это связано с более сложным напряженным состоянием образца. Ком-

32

понента σ3 на поверхности образца равна нулю, но в глубине образца σ3 может иметь значения отличные от нуля, т.е. существует гради-

новских лучей.

В некоторых случаях вместо линейной зависимости εφψ = f(sin2ψ) наблюдается расщепление (рис. 6.2, б), когда точки для φ0, ψ и для φ = φ0+180, ψ лежат на разных кривых ψ+ и ψ−. Анализ показал, что этот эффект связан с необходимостью учета компонентов σ13 и σ23, т.е.

6.3.Обобщённый подход к расчёту тензоров напряжений

идеформации

Вобщем случае соотношение между любым измеренным значением относительной деформации и компонентами тензора деформации определяется с помощью так называемого фундаментального уравнения:

33

где εϕψ – измеренная деформация в направлении, определяемом

углами ϕ и ψ, а ε11, ε12, ε22, ε13, ε23 и ε33 компоненты тензора в системе координат образца Х1Х2Х3, показанной на рис. 6.1 и 6.2.

Подставляя в (6.13) σij вместо εij и вводя рентгеновские упругие постоянные

получим

εϕψ (hkl) = 12 s2 (hkl)[(σ11cos2ϕ+σ12sin2ϕ+σ22sin2ϕ)]sin2ψ+

+12 s2 (hkl)[σ13cosϕ+σ23sinϕ]sin2ψ.

Вуравнении (6.15) сдвиг брэгговского угла или изменение межплоскостного расстояния рассматриваются для каждой ориентации

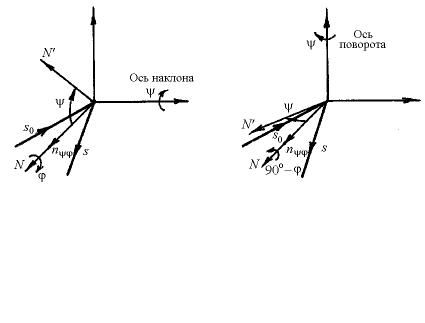
образца (ϕ , ψ). ϕ – определяет угол вращения вокруг нормали к плоскости образца N, а ψ – угол наклона, достигаемый либо путём ψ-вращения вокруг оси наклона на Ψ-дифрактометре, либо вращением вокруг оси поворота на Ω -дифрактометре (рис. 6.3).

Рис. 6.3. Геометрия дифракции для Ψ- (а) и Ω- (б) дифрактометров, предназначенных для измерения остаточных напряжений

34

В Ω-дифрактометре нормаль к поверхности образца в повернутом состоянии N' не является биссектрисой угла между s и s0, поэтому фокусировка по Брэггу–Брентану не выполняется. В тоже время в Ψ-дифрактометре фокусировка по Брэггу–Брентану сохраняется.

Поскольку рентгеновское излучение проникает на некоторую глубину, мы измеряем деформацию <εϕψ>, усреднённую по толщине слоя, участвующего в формировании отражённого пучка s. Тогда уравнение (6.13) нужно записать в следующем виде:

< εϕψ >=< ε11 > cos2ϕ sin2ψ+ < ε12 > sin2ϕ sin2ψ+ < ε22 > sin2ϕ sin2ψ+

Глубину слоя половинного ослабления рентгеновских лучей τ можно записать для Ψ- и Ω-дифрактометров, соответственно, как :

τψ = sinθcosψ/(2μ) (6.18) τω = (sin2 θ−sin2ψ)/(2μsinθcosψ)

где μ – линейный коэффициент поглощения рентгеновского излучения с длиной волны λ.

В изотропной упругой среде напряжение σij и деформация εij связаны следующими выражениями:

σij = [E/(1+ν)]{εij + [ν/(1 – 2ν)](ε11 + ε22 + ε33)δij},

где δij – символ Кронекера.

Из уравнения (6.16) следует, что <εϕψ> является степенной функцией тригонометрических функций углов ϕ и ψ, т.е. <εϕψ> можно выразить через sinnψ или через sin(nϕ) и cos(nϕ), что и составляет основу ψ-дифференциального и ϕ-интегрального методов измерения тензора деформаций. Развитие ψ-дифференциального и ϕ-интегрального методов позволило оценить деформации (εij)0 и их градиенты (εij)(n)= dnεij/dzn в поверхностных слоях образца. Этот метод заключается в разложении <εij(z)> в ряд МакЛарена–Тейлора, как функцию глубины z, т.е.

35

Используя соотношение cos2ψ = 1 – sin2ψ, уравнение (6.18)

Если измерить <εϕψ> для положительных и отрицательных величин ψ, например, – 45° < ψ < + 45°, то можно записать следующие выражения:

Коэффициенты αϕ и βϕ можно оценить по методу наименьших квадратов из графика зависимости (а+)ϕψ от sin2ψ. Коэффициент γϕ можно получить из графика зависимости (а-)ϕψ от sin|2ψ|. При γϕ = 0, уравнение (6.21) описывает sin2ψ-метод.

6.3.2. ϕ-Интегральный метод

Так как глубина слоя половинного поглощения τ (6.18) зависит только от угла наклона образца ψ, можно считать, что <εϕψ> является функцией угла ϕ. Используя соотношения 2cos2ϕ = 1 + cos2ϕ

36

Очевидно, что уравнение (6.24) представляет ряд Фурье, коэффициенты которого можно определить из соотношений:

(An)ψ =(1/π) ∫ <εϕψ> cos(nϕ)dϕ

(Bn)ψ =(1/π) ∫ <εϕψ> sin(nϕ)dϕ, (6.26)

когда деформации <εϕψ> измеряются в диапазоне углов от 0 до 2π. Ниже приведены величины остаточной деформации <εij> и остаточных напряжений <σij>, рассчитанных с использованием уравнения (6.19) и упругих констант Е = 188 ГПа и ν = 0.312 для отражения (310) и Е = 222 ГПа и ν = 0,277 для отражения (211) стально-

го рельса.

Сопоставление приведенных результатов свидетельствует об удовлетворительной точности использованных методов измерения и расчёта компонент тензоров деформаций и напряжений.

37

6.4. Рентгеновские константы упругости в sin2ψ-методе

Фундаментальное уравнение (6.13), (6.15) рентгеновского анализа определения остаточных напряжений в поликристаллических материалах должно учитывать анизотропию упругих констант от направления [hkl] и особенности распределения кристаллитов в образце:

+(ε13cosϕ+ε23sinϕ)sin2ψ+ε33cos2ψ] + s1 (hkl)(σ11 +σ22 +σ33 )] . (6.27)

Для металлов кубической сингонии в приближении Фойгта:

38

где l33 – косинус угла рассматриваемой нормали с нормалью к базисной плоскости.

Коэффициенты упругости cij и податливости sij для некоторых материалов приведены в табл. 5.3, 5.4 и 6.1.

Таблица 6.1

Коэффициенты податливости металлических материалов

(10-6 ГПа-1)

Согласно теории Ройсса упругие константы, используемые в рентгеновских методах измерения макронапряжений, зависят от кристаллографического направления. Замечено, что экспериментальные величины упругих постоянных s1 и 1/2s2 лежат в интервале между значениями, вычисленными с использованием приближений Фойгта и Ройсса (табл. 6.2). Поэтому для расчёта напряжений обычно используют среднее арифметическое (правило Нирфельда) или среднее взвешенное значение упругих констант sV и sR:

39

В табл. 6.2 и 6.3 приведены значения рентгеновских констант упругости для некоторых кубических и гексагональных металлов.

40