Загребаев Методы обработки статистической информации в задачах контроля 2008

Таким образом, результаты проведенных исследований сводятся к следующему:

информативность отдельного датчика уменьшается при увеличении его погрешности;

информативность системы датчиков увеличивается при увеличении числа датчиков в системе;

информативность датчика тем больше, чем больше дисперсия поля в точке его расположения.

Рис. 5.15. Зависимость количества информации о поле в точке расположения датчика от координаты расположения датчика

Зависимость информативности системы датчиков от их расположения. Исследуем зависимость информативности системы датчиков (при заданном их числе ) от их расположения в АЗ.

Результаты исследований представлены на рис. 5.16 и 5.17. Все датчики имеют погрешность 5 %.

Рис. 5.16. График зависимости информативности системы из двух датчиков от координаты при различном расположении датчиков в АЗ: 1 – датчики в точках 1 и 3,5 м; 2 – датчики в

точках 1 и 6 м

371

тической модели). Восстановление проводилось гармоническими функциями.

В табл. 5.8 представлены результаты расчета невязки (5.4.18) для различных наборов датчиков, расположенных в АЗ шириной 7 м.

Таблица 5.8

Результаты расчета невязки

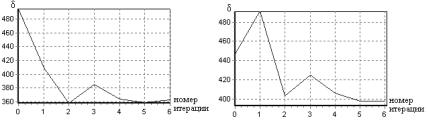
На рис. 5.19 представлена зависимость невязки от номера итерации при нахождении оптимального расположения датчиков методом покоординатного спуска (осуществляется переход от равномерного расположения датчиков к оптимальному).

Рис. 5.19. Зависимость невязки от номера итерации для двух (а) и трех (б) датчиков в системе

Из табл. 5.8 и рис. 5.19 видно, что невязка восстановления поля для оптимального с точки зрения информации расположения датчиков меньше, чем для равномерного расположения. Причем при переходе методом покоординатного спуска от равномерного расположения к оптимальному невязка уменьшается. Таким образом,

374

оптимальное с точки зрения информации расположение датчиков дает более точное восстановление поля.

5.4.5. Восстановление аксиального распределения поля нейтронов в реакторе РБМК при частичной потере измерительной информации

Алгоритмы контроля за распределением поля энерговыделения в реакторе предусматривают ситуации, когда часть датчиков по какой-либо причине выходит из строя [9, 21]. Например, при восстановлении аксиального распределения плотности потока нейтронов, если одна из четырех секций ДКЭВ вышла из строя, то ее показаниями пользоваться запрещено, т.е. секция считается «запрещенной». Сигнал такой секции заменяется на сигнал, рассчитанный определенным образом на основе показаний ближайших ДКЭВ. Если же из строя вышли две и более секции датчика, то датчик полностью считается неработоспособным, подлежащим замене, что не всегда возможно по технологическим соображениям и оправдано по экономическим. Понятно, что если число запрещенных ДКЭВ превысит некоторый предел, то это отрицательно скажется на точности восстановления поля энерговыделения реактора в целом и существенно снизит уровень его безопасности. По этой причине целесообразным представляется разработка алгоритмов, позволяющих восстанавливать поле нейтронов при большем числе отказавших секций, например при двух.

Штатный алгоритм восстановления высотного поля основан на том, что распределение плотности потока нейтронов по высоте аппроксимируется с помощью собственных функций «голого» одномерного реактора:

375

Учитывая, что каждая секция дает интегрированный по ее размеру сигнал Ci , аппроксимационное выражение (5.4.19) приводит-

A

ˆ

где K – матрица m×m .

Таким образом, вектор амплитуд имеет вид

Для обеспечения возможности восстановления аксиального распределения плотности потока нейтронов при выходе из строя части секций датчика предлагается модифицировать штатный алгоритм восстановления за счет корректировки функций разложения. Новые функции разложения предлагается определять по алгоритму, изложенному в разд. 2.5.2, т.е. предлагается перейти от тригонометрического ряда к координатным функциям приближенного канонического разложения. Об эффективности такого подхода можно судить по приведенным ниже данным. Исходным материалом для приведенных ниже оценок являлась информация о токах 66 четырехсекционных датчиков ДКЭВ в 610 временных «срезах». Приближенные координатные функции канонического разложения («естественные» функции), найденные по алгоритму, приведенному в разд. 2.5.2, имеют вид

376

жет быть сделан не единственным образом. Например, некоррелированными являются собственные вектора ковариационной матрицы:

Если на компоненты вектора Z наложить условие, чтобы первая переменная была ориентирована по направлению максимально возможной дисперсии, вторая – по направлению максимально возможной дисперсии в подпространстве, ортогональном первому на-

правлению, и так далее, то в этом случае компоненты вектора Z называют главными компонентами. Координатные функции, полученные по методу главных компонент, имеют вид

(5.4.24)

377

«Естественные» функции и аппроксимирующие функции, рассчитанные по методу главных компонент, имеют вид, изображенный на рис. 5.20.

Рис. 5.20. Вид "естественных" функций (а) и функций, рассчитанных по методу главных компонент (б):

а) 1 − ψ1, 2 − ψ2, 3 − ψ3, 4 − ψ4 ; б) 1 − η1, 2 − η2, 3 − η3, 4 − η4

В качестве критерия, по которому производилось сравнение наборов базисных функций, было выбрано следующее значение невязки в i-й секции ДКЭВ:

где N – число реализаций поля нейтронов (произведение числа временных срезов и числа датчиков); Cit – истинное показание i-й

секции ДКЭВ в t-й реализации, Φˆ ti – рассчитанное показание i-й

секции ДКЭВ в t-й реализации при аппроксимации одним из трех наборов базисных функций (собственные, «естественные», главные компоненты).

Для каждого метода восстановления (для каждого набора функций) и для каждой секции датчика была рассчитана невязка (5.4.25) при запрете различных секций.

Понятно, что при отсутствии запрещенных секций и четырех аппроксимирующих функциях невязка в каждой секции будет равна нулю. Вид восстановленного поля для первой реализации (пер-

378

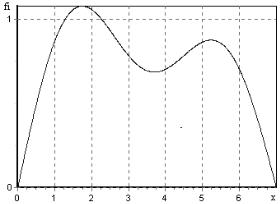
вый датчик, первый временной срез) представлен на рис. 5.21 (все кривые совпадают).

Рис. 5.21. Распределение плотности потока нейтронов по высоте активной зоны

Также были проведены расчеты при отсутствии запрещенных секций, но при меньшем числе аппроксимирующих функций (3, 2, 1). Результаты расчетов приведены в табл. 5.9.

Таблица 5.9

Результаты расчетов невязки (в процентах) при отсутствии запрещенных секций

Из табл. 5.9 видно, что при уменьшении числа аппроксимирующих функций при одном и том же числе разрешенных секций невязка возрастает для каждого набора функций в каждой секции. Но для одного и того же числа функций невязка в любой секции при

379

восстановлении собственными функциями значительно превышает невязку при восстановлении «естественными» функциями и главными компонентами (особенно эта разница видна при малом числе функций – 1 и 2, в этих случаях первая невязка превышает вторую почти на порядок). При этом невязки при восстановлении «естественными» функциями и главными компонентами практически не отличаются.

В табл. 5.10 представлены результаты расчетов при запрете одной секции датчика.

Таблица 5.10

Результаты расчетов невязки (в процентах) при запрете одной секции

Из табл. 5.10 видно, что при запрете одной секции и восстановлении тремя функциями невязка отлична от нуля только в запрещенной секции, т.е. восстановление по достаточному числу измерений во всех остальных секциях не зависит от отказа одной секции. Однако при использовании меньшего числа функций невязка возрастает. Также из табл. 5.10 видно, что при аппроксимации собственными и «естественными» функциями наименьшая невязка возникает при запрете средних секций (2-й и 3-й), а при аппроксимации функциями, рассчитанными по методу главных компонент, наименьшие невязки возникают при запрете крайних левых секций (1-й и 2-й). Вид поля при запрете 3-й секции представлен на рис. 5.22.

380