
- •1. ‘Chronicle’ of diamagnetic exciton
- •2. Proof of the exciton nature of the oscillating magnetoabsorption
- •3. The concept of ‘diamagnetic excitons’
- •4. Quasi-Landau magnetic spectroscopy of the ‘Rydberg’ exciton states
- •5. Developing the concept of Quasi-Landau magnetoabsorption by the exciton ‘Rydberg’ states in semiconductors: InP, GaAs and CdTe (years 1990–94)
- •6. Diamagnetic excitons in hexagonal crystals
- •7.2. Proof of exciton participation in the formation of magneto-optical spectra of PbTe (1986)
- •8. Observation of the diamagnetic-exciton spectra in semiconductor solid solutions
- •9. Development of the diamagnetic-exciton concept and its application to a broad range of semiconductor crystals
- •10.2. Observation of above-barrier exciton and its magneto-optics (1996–2000) [44]
- •11. Exciton polariton and its role in the interband magneto-optics of semiconductors
- •12. Polariton nature of the diamagnetic exciton
- •14. Magneto-quantum exciton polymer
- •15. Conclusion
- •References

Home Search Collections Journals About Contact us My IOPscience
Diamagnetic excitons and exciton magnetopolaritons in semiconductors
This article has been downloaded from IOPscience. Please scroll down to see the full text article.
2012 Semicond. Sci. Technol. 27 053001
(http://iopscience.iop.org/0268-1242/27/5/053001)
View the table of contents for this issue, or go to the journal homepage for more
Download details:
IP Address: 194.85.224.35
The article was downloaded on 25/04/2012 at 14:44
Please note that terms and conditions apply.

IOP PUBLISHING |
SEMICONDUCTOR SCIENCE AND TECHNOLOGY |
Semicond. Sci. Technol. 27 (2012) 053001 (24pp) |
doi:10.1088/0268-1242/27/5/053001 |
TOPICAL REVIEW
Diamagnetic excitons and exciton magnetopolaritons in semiconductors
R P Seisyan
Ioffe Physical-Technical Institute, Russian Academy of Sciences, 194021 St. Petersburg,
Russia
E-mail: rseis@ffm.ioffe.ru
Received 12 October 2011, in final form 17 January 2012
Published 19 April 2012
Online at stacks.iop.org/SST/27/053001
Abstract
Interband magneto-absorption in semiconductors is reviewed in the light of the diamagnetic exciton (DE) concept. Beginning with a proof of the exciton nature of oscillating-magnetoabsorption (the DE discovery), development of the DE concept is discussed, including definition of observation conditions, quasi-cubic approximation for hexagonal crystals, quantum-well effects in artificial structures, and comprehension of an important role of the DE polariton. The successful use of the concept application to a broad range of substances is reviewed, namely quasi-Landau magnetic spectroscopy of the ‘Rydberg’ exciton states in cubic semiconductors such as InP and GaAs and in hexagonal ones such as CdSe, the proof of exciton participation in the formation of optical spectra in narrow-gap semiconductors such as InSb, InAs, and, especially, PbTe, observation of DE spectra in semiconductor solid solutions like InGaAs. The most fundamental findings of the DE spectroscopy for various quantum systems are brought together, including the ‘Coulomb-well’ effect, fine structure of discrete oscillatory states in the InGaAs/GaAs multiple quantum wells, the magneto-optical observation of above-barrier exciton. Prospects of the DE physics in ultrahigh magnetic field are discussed, including technological creation of controllable low-dimensional objects with extreme oscillator strengths, formation of magneto-quantum exciton polymer, and even modelling of the hydrogen behaviour in the atmosphere of a neutron star.
1. ‘Chronicle’ of diamagnetic exciton
The first observation of the diamagnetic-exciton effect was presumably made by Zakharchenya [1]. In as far back as 1956, he studied the spectrum of the Wannier–Mott exciton in copper oxide crystals, making use of high electric and magnetic fields (see figure 1). In addition to the expected Stark and Zeeman effects, he has noted that there is a new unknown and unexpected phenomenon, namely slight periodic oscillations in the continuum (continuous absorption edge). Those oscillations had the frequency of the cyclotron resonance, which was reflected in the title of the article by Gross, Zakharchenya and Pavinskiy: ‘Diamagnetic levels of an exciton in Cu2O and cyclotron resonance’ published in 1957 [2]. Almost simultaneously, two articles went out in
1957 too, that belonged to American authors, Burstein and Picus [3] and Lax and Zwerdling [4] who had observed the magnetic-field absorption-continuum oscillations in indium antimonide and germanium, respectively. Excitons either in germanium or in indium-antimonide crystals had not been observed by that time (in germanium crystals that happened in 2 years [5], and in InSb in 22 years [6]). That is why the effect was unambiguously attributed to the continuum-density oscillations associated with the appearance of the Landau levels. No reference to the excitons or, accordingly, to the article [2] was made.
Works [3] and [4] have caused an unprecedented boom in magneto-optical studies of semiconductors. This helped to fill most of the data bank on the parameters of the band structure of the significant semiconductor crystals.
0268-1242/12/053001+24$33.00 |
1 |
© 2012 IOP Publishing Ltd Printed in the UK & the USA |

Semicond. Sci. Technol. 27 (2012) 053001 |
Topical Review |
(a)
(b)
(c)
(d )
Figure 1. Spectroscopic photos of cuprous-oxide yellow series (a), the same if placed in a high electric field (b) or in a high magnetic field (c). Eg or n0 = ∞ correspond to 2.17244 eV. (d) The first observation of the oscillating magnetoabsorption. Spectral intensity variations are symbolically shown as undulations of the top border to guide the eye.
2. Proof of the exciton nature of the oscillating magnetoabsorption
Naturally, there appeared a task to find indisputable evidence for the exciton nature of this effect. Zakharchenya formulated this objective to the author of this work, a graduate student of the Ioffe Institute at that time. Provided that the commonly accepted interpretation of the phenomenon had been correct, there was seemingly full compliance with the requirements for the effect observability. However, an initial attempt to solve the problem with the use of a promising new semiconductor, gallium arsenide, did not produce results. In magnetic fields available at that time, the GaAs absorption edge remained smooth without any signs of oscillatory behaviour. This prompted us to perform test experiments with germanium crystals. Reproducing the experimental conditions of paper [4], we tried to find the necessary proofs in Ge first. We built a proof making use of three specific properties of the exciton absorption. First, excited states in the exciton spectrum can
belong to different principal quantum numbers of the exciton. Second, the exciton states can be suppressed by the screening of the Coulomb interaction between the electron and hole. Third, a high magnetic field makes exciton ‘one-dimensional’, providing it with properties of a one-dimensional (1D) state. Figure 2 shows both the spectrum of oscillating magnetoabsorption (OMA) in germanium crystals registered by us [7] and its modulated form obtained under the electric-field influence. There were additional weak peaks which could not be presumably (because of their energy positions) assigned either to the ground states of the exciton or to transitions between the Landau subbands. They could be most likely attributed to the excited states of exciton. In order to find out their nature, we applied the electric field parallel to the magnetic one (E//B). In this configuration, the electric field does not affect the energy positions of the peaks. In differential spectrum, these weak peaks grow with modulated electric field almost to the level of the ground state peak. Since the intensities of lines correspond here to the states’ sensitivities
2

Semicond. Sci. Technol. 27 (2012) 053001 |
Topical Review |
Figure 2. Oscillations in germanium registered under conditions close to those in experiments by Zwerdling and Lax [4]. The Faraday geometry, T = 4.2 K, B = 6 T. Transitions: (I) a+(l)ac(l+1), (II) b+(l)bc(l+1), (III) a−(l)ac(l+1), (IV) b−(l)bc(l+1). Hereinafter, the following notification for the Landau subband systems is used in the text : ac and bc—electrons with spin projections on the magnetic-field direction +1/2 and −1/2, correspondingly); a− and b−—heavy holes and a+ and b+ light holes with momentum projection M = ± 3/2 and
± 1/2, accordingly. The right part shows the low-energy fragment of this spectrum (π -polarization, B = 3.4 T) in comparison with the differential spectrum (modulation by the electric field E//B). The vertical lines correspond to the theoretical positions of the first DE transitions with the electron Landau quantum numbers lc = 0, 1 and 2. Numeration gives serial numbers of spectral lines. Positions of DE excited states are marked with arrows.
to modulating field (the more the sensitivity the more the radius of the state a ), this effect has shown the exciton nature of the excited and ground states.
As a rule, the Coulomb interaction in an electron–hole pair can not be completely ‘turned off’ and exists in any of the cases of interband magneto-optical spectra. It can be destroyed only by screening with the charges of opposite signs. The condition of the complete screening can be written as a > rscr, where rscr is the radius of the Debye–Hueckel screening. Depending on the exciton-state nonstationarity due to the exciton– scatterer interaction, screening charges and electric fields, there are various state lifetimes and the corresponding line widths. The latter predetermine the possibility of registering spectral lines from the excited states of the exciton series or of bound states in general. Magnetic field modifies the interaction of excitons with free carriers and defects, resulting mainly in the stabilization of the exciton states. Moreover, in a high magnetic field reducing the problem to a 1D model, there may already be arbitrarily weak bound state. A magnetic field application leads to a general ‘flare-up’ of absorption up to the values which correspond to those of the pure crystal on the average [8].
The effect of the exciton-absorption ‘flare-up’ in a magnetic field is illustrated by figure 3. It shows a general rise of the absorption level with increasing magnetic field in the germanium crystal doped up to the critical concentration ND ≈ 8 1015 cm−3. In the case of a crystal doped above this
Figure 3. Signal proportional to the absorption intensity at different values of the magnetic field (‘flare-up effect’) for Ge samples with critical impurity concentration, Nd = 8 1015 cm−3. The dashed line shows the average level of absorption.
critical concentration, the total absorption at the edge (as a function of the incident radiation) is much lower than that in an undoped crystal without magnetic field.
3. The concept of ‘diamagnetic excitons’
Further investigations of both the OMA and exciton in semiconductors in a high magnetic field have enabled us to
3
Semicond. Sci. Technol. 27 (2012) 053001 |
Topical Review |
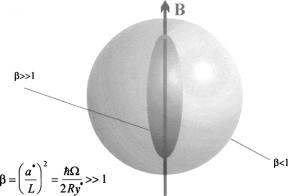
Figure 4. Schematic representation of the ground-state wavefunction of the Wannier–Mott exciton (the sphere), the same for the diamagnetic exciton (the ellipsoid of rotation inside the sphere), and the Elliott–Loudon criterion.
formulate the concept of the ‘diamagnetic exciton’ (DE) [9]. We have given such a name to special exciton states arising from the placement of the Wannier–Mott exciton in a high magnetic field. The criterion of the high magnetic field is the Elliott–Loudon criterion [10] (see figure 4):
β |
= |
(a /L)2 |
= |
/2Ry |
≡ |
(ε2 |
3/μ2e3c)B |
|
1 (1) |
|
|
|
0 |
|
|
where a = ( 2/e2 ) (ε0/μ), = ωcc + ωcv ≡ eB/μc is the sum of the cyclotron frequencies of electron and hole, and
Ry = μe4/2 2ε02 is the effective Rydberg of the Wannier– Mott exciton. The DE state energies in the magnetic field are
EB = ElM − R∞(1) (ν + δνug)2, ν = 0, 1, etc. (2)
Here ElM represents a series of transitions between the Landau levels without taking into account the Coulomb electron–hole interaction, ν is the principal quantum number of the one-dimensional exciton and the quantum defect δνug is a correction of ν for the finiteness of the magnetic field B. ElM depends on the Landau number l, moment projection M and magnetic field B. The effective Rydberg of the 1D exciton R∞(1) also turns out to be a function of l, M, and even B through the 1D reduced mass in the most common case. The quasidiscrete spectrum of these exciton states is clearly not restricted by the edge of absorption Eg as in the three-dimensional case. That is to say, it is stretched far into the region E > Eg.
Thus, the spectrum of hydrogen-like system in a high magnetic field can be described as follows. First, there is a sequence of the Landau subbands interacting in optical transitions. Second, each pair of subbands is accompanied by a singlet (ν = 0) and a number of doublet levels (ν > 0). Finally, these levels form Coulomb series for the large enough ν. With increasing magnetic field B, quantum defects δνug decrease. This, in its turn, leads to the increase of binding energy of the vth state. The binding energy of the ground state (ν = 0) increases infinitely (but logarithmically slowly) with B, what corresponds to a collapse to the centre. Figure 5 illustrates the overall picture of magneto-optical effects in the transitions between the Landau subbands and in transitions into DE states.
4. Quasi-Landau magnetic spectroscopy of the ‘Rydberg’ exciton states
The DE concept has been developed in detail for diamond-like semiconductor crystals in particular [11]. It has allowed us to satisfactorily explain and describe most of the available experimental data. The band structure parameters thus obtained for various semiconductors are of especial value.
However, it should be noted that this concept has proved to be inefficient to explain and simulate the magneto-optical data on some relatively wide-gap semiconductor crystals. In particular, it does not work in the very copper oxide, which the DE history began with. The crucial feature of this case is the existence of expanded series of the Wannier–Mott exciton even before the application of a magnetic field. As is well known, the copper oxide is unique in this respect. There are many excited (Rydberg) states of the hydrogen-like exciton series (up to the principal quantum number n0 = 10!) observed in the optical spectrum of the absorption edge of the most perfect samples. The inferior members of the series exhibit low-field effects, such as the Stark and Zeeman effects and diamagnetic shift, whereas the superior ones come to the dissociation edge as a result of the giant diamagnetic shift. The latter states form the oscillations of the continuum (a high-field effect). Along with copper oxide, ‘lengthy’ series were previously observed also in the tin oxide [12] and some other crystals.
Registration of ‘lengthy’ series is especially difficult in the case of diamond-like semiconductors with allowed direct interband transitions. It requires not only the material of the highest crystal-physical perfection but also the ability to produce extremely thin samples with thicknesses approximating the absorption length d αmax−1 (from submicrons to several microns). In doing this, defects or nonuniform stresses should not be brought in, and the density of surface states should be kept minimum.
For the first time in the case of diamond-like semiconductors, we have succeeded to do it when we used relatively ‘thick’ homoepitaxial layers of GaAs, which showed the low-temperature electron mobility (1–2) × 105 cm2 (V s)−1. The mechanical treatment, chemical etching and annealing in pure hydrogen had been consecutively applied. During the measurements, the samples were placed in special boxes of the cover glass. Next, they were deposited in the evacuated liquid helium immediately in a cryostat. Using these samples, the first ‘lengthy’ series of the Wannier–Mott GaAs exciton were registered. Without magnetic field, it included the states with principal quantum numbers n0 = 1, 2 and 3 and quasi continuum at n0 3 (see figure 6). Placing these samples in a high magnetic field made it possible to observe unique spectra of magnetoabsorption (see figure 7). These spectra had a number of fundamental features, being the DE spectra in fact. Their interpretation required the application of both the quasi-one-dimensional DE-series concept and a theory of transitions obeying various additional selection rules [13, 14]. In these spectra, the Fano resonances were also first observed. These resonances are characteristic of the interaction of the discrete DE states with its own 1D continuum. This was first noted by Chemla (see paper [15]) who analysed our spectra
4
