
Кур_тех_07
.pdfФедеральное агентство по образованию
ГОУ ВПО Кубанский государственный технологический университет (КубГТУ)
Кафедра автоматизации производственных процессов
Курсовая работа
по дисциплине: «Автоматизированные системы управления технологическими процессами» на тему: Проектирование и анализ работы одноконтурной непрерывной и цифровой систем автоматического управления
Задания и методические указания.
Для студентов дневной форм обучения факультетов: Инженерии и экспертизы продуктов питания, Биотехнологии и ресторанного бизнеса, специальностей:
260401 – Технология жиров, эфирных масел и парфюмернокосметических продуктов
260204 - Технология бродильных производств и виноделие;
260301 - Технология мяса и мясных продуктов;
260302 - Технология рыбы и рыбных продуктов;
260303 - Технология молока и молочных продуктов
Краснодар
2007 г.
Составитель: канд.техн.наук, доцент В.И.Пугачев УДК 621.007(07)
Курсовая работа
Задания и методические указания на курсовую работу по дисциплине «Автоматизированные системы управления технологическими процессами» для студентов дневной форм обучения факультетов: Инженерии и экспертизы продуктов питания, Биотехнологии и ресторанного бизнеса,
специальностей: 260401, 260204, 260301, 260302, 260303 / Сост: В. И. Пу-
гачев; Кубан. Гос.техн. ун-т. Каф. Автоматизации производственных процессов. – Краснодар: Изд-во КубГТУ, 2007. – 34 с.
Приведены задания и методические указания к курсовым работам, а также список рекомендованной литературы.
Ил. 6. Библиогр. 7 назв.
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета
Рецензенты:
д-р техн.наук профессор зав.кафедрой МТМ и РП факультета пищевых биотехнологий и ресторанного бизнеса КубГТУ Г.И. Касьянов
канд. техн. наук, доцент каф. АПП КубГТУ |
С.А. Подгорный |
2
Курсовая работа имеет цель – ознакомление с основными направлениями работ, проводимых при автоматизации производственных процессов. Современные средства автоматизации предполагают использование микропроцессорных средств управления, поэтому, наряду с вопросами проектирования, необходимо иметь представление о методах описания и расчета цифровых систем управления, как наиболее употребляемых в настоящее время в проектных решениях и перспективных для автоматизации в будущем.
Знание указанных особенностей поможет будущим инженерам – технологам участвовать в разработке заданий на автоматизацию, разрабатываемых ими технологических процессов.
1 Задания на курсовую работу
Вариант курсовой работы студент-технолог получает от преподавателя, проводящего консультации по курсовой работе.
1 Запроектировать систему автоматического контроля и управления объекта с двумя выходными величинами и составить схему автоматизации с использованием ЭВМ или микроконтроллера. Регулируемая величина определяется по предпоследней, а контролируемая по последней цифре номера варианта.
Вариант задания определяется по двум последним цифрам номера зачетной книжки, или задается преподавателем, ведущим курсовую работу.
Таблица 1 Последняя и предпоПараметры контроля и управления
следняя цифра варианта
1 |
Плотность |
2 |
Влажность |
3 |
Соотношение расходов |
4 |
Уровень сыпучего вещества |
5 |
Уровень жидкости |
6 |
Давление |
7 |
Расход сыпучего вещества |
8 |
Вязкость |
9 |
Расход жидкости |
0 |
Температура |
Объект должен относиться к известному Вам технологическому процессу пищевой или химической промышленности.
Для запроектированной системы автоматического управления, изображенной на рисунке, произвести расчеты:
3
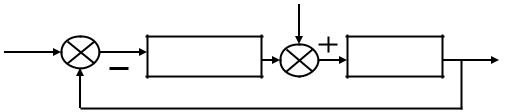
1 Найти передаточную функцию разомкнутой системы управления, а
также замкнутой по каналу ϕ3 → ϕ .
2 Проанализировать устойчивость замкнутой системы по критерию Найквиста-Михайлова. Определить запас устойчивости замкнутой САУ по модулю и фазе.
3 Используя критерий Гурвица, найти область устойчивых параметров системы, указанных в задании.
4 Выбрав значения параметров из области устойчивости, определить
статическую ошибку регулирования при ϕ3 =1(t) и λ =1(t).
5 Найти выражение переходной функции замкнутой системы по каналу ϕ3→ϕ и построить ее график.
6Для рассмотренной системы, используя параметры из области устойчивости, найти период дискретности измерений выходной величины, обеспечивающий ее измерение без потери информации.
7Произвести пересчет параметров регулятора, выбранных из области устойчивости в параметры цифрового фильтра с расчетным периодом квантования. Если параметр объекта изменен, то его и следует применять в дальнейших расчетах.
8Построить переходный процесс в цифровой системе на единичное ступенчатое входное воздействие по заданию ϕ3 =1(t).
9Сравнить качество переходных процессов в непрерывной и цифровой системах по параметрам: длительность переходного процесса, относительная степень затухания, динамический заброс.
ϕ3 |
|
λ |
Wp ( p ) |
ϕ |
|
|
Wo ( p ) |
Рисунок 1 – Структурная схема системы управления
Требования к оформлению курсовой работы:
титульный лист должен содержать информацию, указанную в приложении
1;
дальше должно следовать задание на курсовую работу с указанием конкретных параметров варианта и расчетной схемы;
каждый пункт выполнения должен содержать основные теоретические предпосылки, конкретные пояснения и результаты расчетов, приводимые графики должны быть табулированы;
в конце пояснительной записки необходимо привести список использованной литературы и поставить свою роспись и число.
4
Таблица 1 ( Первая цифра номера варианта)
N |
K1 |
K2 |
T1 |
Td |
T2 |
T3 |
T4 |
T5 |
0 |
1,0 |
1,2 |
10 |
3.0 |
6,0 |
1 1 |
6.0 |
1 |
1 |
1,5 |
1,3 |
13 |
2.0 |
13,13 |
17.75 |
7.5 |
1.1 |
2 |
2,0 |
1,4 |
15 |
2.5 |
9,0 |
13.5 |
6.5 |
1.2 |
3 |
2,5 |
1,5 |
17 |
3.0 |
15 |
18.5 |
7.5 |
1.3 |
4 |
3,0 |
1,6 |
19 |
3.5 |
18 |
27 |
10 |
0.5 |
5 |
3,5 |
1,5 |
20 |
4.0 |
21 |
25.25 |
9 |
0.7 |
6 |
3,0 |
1,4 |
18 |
3.2 |
22.5 |
25.25 |
9 |
0.9 |
7 |
2,5 |
1,3 |
14 |
2.8 |
26.25 |
26.75 |
9 |
0.3 |
8 |
2,0 |
1,2 |
12 |
1.2 |
30 |
29.5 |
9.5 |
1.4 |
9 |
1,5 |
2,0 |
16 |
2.2 |
60 |
47 |
10 |
0.8 |
Таблица 2 |
(Вторая цифра варианта) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры |
Вар. |
|
|
Wp(p) |
|
|
|
|
|
|
|
|
|
Wo(p) |
|
|
|
|
|
|
|
|
|
|
системы |
|||||
|
|
K1 |
+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
T p+1 |
|
|
|
|
|
|
|
|
|
|
K ,T |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
1 1 |
|||||||||
0 |
|
T1 p |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
T p2+T p+1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
T1,K2 |
1 |
|
|
|
|
T1p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
T p3+T p2+T p+1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
K1 + Td p |
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
K1,Td |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T p3+T p2 |
+T p |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
4 |
|
|
|
|
|
|
||||
|
K + |
|
1 |
|
|
+ T p |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
K1,T1 |
||||
3 |
T1p |
|
|
|
|
|
T p2+T p+1 |
|
|
|
|||||||||||||||||||
|
1 |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
K + |
|
1 |
|
|
+ T p |
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
K1,T1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
|
1 |
|
T1p |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
T p2+T p+1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
K1 + Td p |
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
K1,Td |
|||||
|
|
|
|
|
|
|
|
|
|
|
T |
2 |
p3 +T p2 +T |
4 |
|
|
p+1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
K1 |
|
|
|
|
|
|
|
|
|
|
T5 p+1 |
|
|
|
|
|
|
|
|
|
|
K1,T5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T p3 |
+T p2 |
+T p |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
4 |
|
|
|
|
|
|
||||
7 |
|
|
|
|
K1 |
|
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
K1,K2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
T p3+T p2+T p+1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
K1 |
+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
K ,T |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|||||||||
8 |
|
T1 p |
|
|
|
|
|
|
T3 p2+T4 p+1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5
|
|
1 |
|
|
T5 p +1 |
T1,T2 |
|||
9 |
T1p |
||||||||
|
|
T p2 |
+ T p +1 |
|
|
||||
|
|
|
|
2 |
3 |
|
|
||
2 Методические указания для выполнения курсовой работы
При выполнении первого пункта курсовой работы следует использовать рекомендации, изложенные в [1], приложениях 2,3.
Кратко изложив технологию проектируемого процесса и технологический регламент (значения измеряемой и регулируемой величин), необходимо выбрать измерительные приборы для контролируемой и регулируемой величин, а также исполнительный механизм для перемещения регулирующего органа в системе управления.
Спецификацию выбранных измерительных приборов и исполнительного механизма следует привести в виде таблицы, показанной ниже.
Поз. |
Наименование, тип изме- |
К-во |
Примечание |
|
обозначение |
рительного прибора |
|
|
|
|
Термопреобразователь |
|
-50-50 гр.С, четырехпро- |
|
1-1 |
сопротивления, |
ТСП- |
1 |
водная схема включения |
|
0139-1-320 |
|
|
|
1-2 |
|
|
|
|
Последующие пункты освещены в [2,4] и кратко представлены ниже. При выполнении курсовой работы могут быть использованы програм-
мы, приведенные в [3], или примеры выполнения, изложенные в [5].
2.1 Структурные преобразования САУ
При анализе САУ любой сложности приходится изменять ее структуру не изменяя свойств в целях удобства исследования или наглядности, необходимости моделирования или выбора корректирующих звеньев. При этом следует пользоваться следующими очевидными правилами:
при последовательном включении звеньев их результирующая передаточная функция равна произведению передаточных функций отдельных звеньев;
при параллельном включении звеньев результирующая передаточная функция равна сумме передаточных функций отдельных звеньев;
при встречно-параллельном включении звеньев результирующая передаточная функция равна частному от деления передаточной функции прямой связи на единицу плюс или минус передаточная функция разомкнутого контура, в котором звенья включены встречно-параллельно (рисунок 2).
6
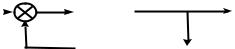
При этом знак «плюс» соответствует отрицательной, а «минус» - положительной обратной связи. Для схемы (рисунок 2) справедливы соотношения:
x1 (p) = x вх ± x 2 (p); x вых (p) = x1 (p)W1 (p); x2 (p) = x выхW2 (p) .
Хвх |
Х1 |
|
|
Хвых |
||
Wp(p) |
||||||
|
|
|
||||
|
± |
|
|
|||
Х2 |
|
|
|
|
||
|
|
|
|
|||
|
|
Wo(p |
|
|
||
|
|
|
|
|||
|
|
|
|
|||
Рисунок 2 – Встречно- |
|
|
||||
параллельное включение звеньев |
||||||
Исключив из этой системы уравнений промежуточные переменные x1 и x2 , получим
W (p) = |
|
|
W1 (p) |
= |
x вых (p) |
. |
(1) |
|
|
|
|
||||
3 |
1 |
± W1 (p)W2 (p) |
|
x вх (p) |
|
||
|
|
|
|||||
2.2Критерий устойчивости Найквиста - Михайлова
Спомощью критерия устойчивости Найквиста-Михайлова по стационарным свойствам разомкнутой САУ можно судить о нестационарных свойствах замкнутой.
Известно, что характеристическое уравнение замкнутой САУ, определяющее ее устойчивость, получается приравниванием нулю знаменателя
передаточной функции замкнутой системы, т.е. 1 + Wраз (p) = 0 .
Обозначим W (p) = |
Q(p) |
, тогда1 + W (p) = |
Q(p) + P(p) |
. |
(2) |
P(p) |
|
||||
раз |
раз |
P(p) |
|
||
|
|
|
|
||
Если в выражении (2) заменить p на jω , то в числителе получим го-
дограф Михайлова для замкнутой системы, а в знаменателе - для разомкнутой. При этом степень числителя и знаменателя будут одинаковы и, если замкнутая и разомкнутая системы устойчивы, то
arg [1 + Wраз ( jω)] = |
arg [Q( j) + P( jω)] − |
arg |
P( jω) = n π − n π = 0. |
|
0<ω<+∞ |
0<ω<+∞ |
0<ω<+∞ |
2 |
2 |
На комплексной плоскости это обозначает, что вектор 1 + Wраз ( jω) при изменении ω от 0 до + ∞ не поворачивается вокруг точки − 1, j0 , или вектор Wраз ( jω) не охватывает на комплексной плоскости точку − 1, j0
при изменении ω от 0 до + ∞ (рисунок 3).
Таким образом, если разомкнутая САУ устойчива и ее АФХ не охватывает на комплексной плоскости точку с координатами − 1, j0 , то замкнутая САУ будет устойчива.
7
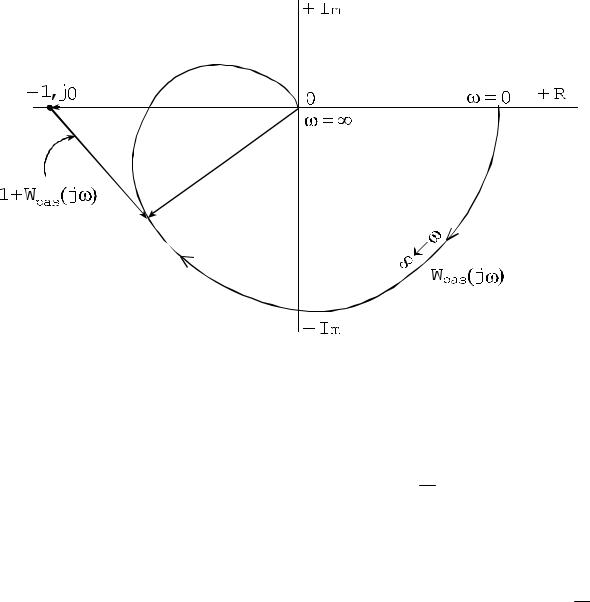
Рисунок 3 – |
К обоснованию критерия Найквиста-Михайлова |
|||
Если разомкнутая САУ неустойчива и имеет m неустойчивых кор- |
||||
ней, а замкнутая САУ устойчива, то |
|
|
|
|
arg [1 + Wраз ( jϖ)] = n π − (n − m) π + m π = m 2π. |
||||
0<ϖ<+∞ |
2 |
2 |
2 |
2 |
Таким образом, если разомкнутая САУ неустойчива и имеет m не- |
||||
устойчивых корней, то для устойчивости САУ в замкнутом состоянии не- |
||||
обходимо, чтобы АФХ разомкнутой системы охватывала в положительном |
||||
направлении точку на комплексной плоскости с координатами (−1, j0) m 2
раз.
Если разомкнутая САУ неустойчива, то число неустойчивых корней можно определить по критерию Михайлова.
В том случае, если разомкнутая САУ находится на границе устойчивости благодаря наличию нулевых корней, передаточную функцию ее можно записать так:
|
W |
(p) = |
|
Q(p) |
, |
(3) |
|
|
|
|
|||||
|
|
раз |
|
P |
ν P (p) |
|
|
|
|
|
|
|
|||
|
ν P |
(p) = P(p); |
1 |
|
|
||
где P |
ν - кратность нулевого корня. |
|
|||||
|
1 |
|
|
|
|
|
|
При малых значениях ω АФХ нейтральной системы можно представить так:
8
|
Wраз |
(p) = |
|
b |
0 ( jv)m + b1 ( jv)m−1 +K+b m |
|
» |
|
|
||||||||||||
|
( jv) |
ν [a 0 ( jv)n + a1 ( jv)n−1 +K+a n ] |
|
(4) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
» |
b m |
× |
1 |
|
= |
|
A |
e− jν 2 |
= |
A |
e− jϕ(ω) , |
|
|
|
|||||||
|
|
|
( jv)ν |
|
|
|
|
|
|||||||||||||
|
|
a m |
|
|
|
|
vν |
|
vν |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
||||
где A = |
b m |
; |
|
1 |
|
= e− jν 2 . |
|
|
|
|
|
|
|
||||||||
|
|
jν |
|
|
|
|
|
|
|
|
|||||||||||
|
a m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из выражения (4) следует, что при малых ϖ значение |
A |
→ ∞ . АФХ |
|||||||||||||||||||
ϖ ν |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
разомкнутой системы стремится к началу координат при увеличении ϖ по одной из осей координат комплексной плоскости:
при ν = 1 |
ϕ(0) = − π , т.е. АФХ перемещается по отрицательной мнимой |
|||
|
|
2 |
|
|
оси; |
ν = 2 |
ϕ(0) = −π, т.е. АФХ перемещается по отрицательной вещест- |
||
при |
||||
венной оси; |
||||
при |
ν = 3 |
ϕ(0) = − |
3π |
, т.е. АФХ перемещается по положительной мни- |
|
||||
|
|
2 |
|
|
мой оси.
Для анализа устойчивости таких систем справедлив критерий устойчивости Найквиста-Михайлова, если их АФХ дополнить частью окружности бесконечного радиуса, которая начинается на положительной вещественной полуоси.
Запас устойчивости замкнутой системы по модулю определяется величиной обратной расстоянию от начала координат до точки первого пересечения АФХ разомкнутой СУ с отрицательной вещественной осью.
Запас устойчивости замкнутой системы по фазе определяется углом между отрицательной вещественной осью и направлением луча, выходящего из начала координат в точку пересечения АФХ с единичной окружностью с центром в начале координат.
2.3 Граница и область устойчивости для одного и двух параметров
Для выделения области параметров, обеспечивающих устойчивую работу САУ, используются критерии устойчивости. Рассмотрим применение для выделения области устойчивости по одному и двум параметрам критерия Гурвица.
Пусть САУ имеет один параметр настройки α . Для выделения области значений α , обеспечивающих устойчивость САУ запишем все условия ус-
9
тойчивости - положительность всех главных диагональных миноров до « n − 1» при a 0 > 0 . В частном случае α может входить и в a 0 . Равенство
нулю миноров соответствует границе устойчивости.
Если построить зависимости 1 = f1(α), 2 = f2(α), K, n−1 = fn−1(α), то значе-
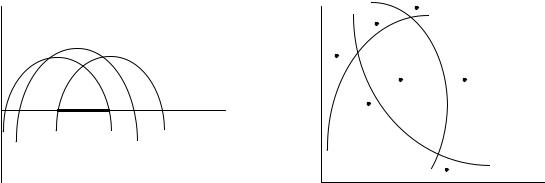
ния параметра α , удовлетворяющие условию устойчивости, будет лежать на оси абсцисс в той области значений α , для которых миноры положительны (рисунок 3).
|
Если САУ имеет два параметра настройки α и β , то приравняв ну- |
лю |
1 (α, β) = 0, 2 (α,β) = 0, K , n−1 (α, β) = 0, получим "n" уравнение |
границы устойчивости в плоскости двух параметров. Задаваясь значениями одной из них, по каждому уравнению можно найти значение другого и построить линии границы устойчивости. При этом плоскость параметров α и β будет разделена на области. Для определения области, удовлетво-
ряющей условию устойчивости, необходимо из каждой области взять одну точку и проверить на устойчивость (рисунок 4).
САУ находится на границе устойчивости, если характеристическое уравнение имеет нулевые или мнимые корни.
= f (α) |
2 = 0 |
α 1 =0 |
|
1 |
2 |
|
|
α y |
3 |
α |
3 = 0
β
Рисунок 4 – Пример выделения области устойчивости по критерию Гурвица
2.4 Ошибки управления и их составляющие в СУ
Устойчивость САУ является необходимым условием ее применения, но недостаточным. Системы работают в различных режимах и при различных входных воздействиях. При этом качество системы оценивается по величине ошибки ε , получаемой в процессе работы, которая должна быть меньше допустимой (рисунок 5):
ε(р) = ϕ 3 (t) − ϕ u (t)
10
