Вопрос № 22 Аналогия между электрическим полем в проводящей среде и электростатическим полем в диэлектрике.

(4)

получим:

(5)

Сравнив уравнение (5) с уравнением электростатики, можно установить аналогию между электрическим полем постоянных токов в проводнике и электрическим полем в диэлектрике.

Электростатическое поле	Электрическое поле в проводящей среде
rot E = 0	rot (E - Eс) = 0
D
Pr

Из этой таблицы видно, что аналогом вектора плотности тока проводимости является вектор электрического смещения D, аналогом удельной проводимости - абсолютная диэлектрическая проницаемость, аналогом тока I - поток вектора электрического смещения; аналогом заряда в электростатическом поле являются стоки сторонних электрических токов.

Вопрос № 23 Расчет тока утечки, сопротивления изоляции коаксиального кабеля.

Вопрос № 24 Расчет поля тока шарообразного заземлителя. Сопротивление заземления.

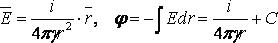, если принять , то постоянная интегрирования С=0.

Потенциал на поверхности заземлителя при r = R:

 ,

откуда получаем формулы для сопротивления заземлителя и его тока:

.

Пример 2. Заземлитель в виде шара расположен на сравнительно небольшой глубине h, соизмеримой с его радиусом R (рис. 271).

 

Применим к решению задачи метод зеркальных отображений. Заменим в верхней полуплоскости диэлектрик  проводящей средой γ и зеркально расположим там такой же заземлитель той же полярности, при этом граничные условия на поверхности земли не изменятся (линии вектора Е направлены по касательной вдоль поверхности). Заменим токи, стекающие с поверхностей обоих заземлителей, равными по величине точечными токами, растекающимися из электрических центров 1 и 2, которые будут смещены относительно геометрических центров так, чтобы сохранились прежними граничные условия на поверхности шаров (поверхности должны остаться эквипотенциальными с потенциалом φ=U). После определения положения электрических центров расчет параметров поля в произвольной точке n производится по методу наложения:

.

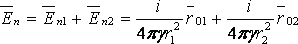
При соотношении h>>R потенциал на поверхности заземлителя будет равен:

, откуда следует формула для определения сопротивления заземлителя:

.

Вопрос № 25 Магнитное поле постоянного тока, его уравнения, граничные условия.

Уравнения Максвелла в интегральной форме 1)

2)

3)

4)

Уравнения Максвелла в дифференциальной форме

1)

2)

3)

4)

Граничные условия

Но можно достигнуть полной математической эквивалентности обеих форм уравнений Максвелла. Для этого ДИФФЕР. УР-Я надо дополнить граничными условиями, которым должно удовлетворять ЭМ поле на границе раздела 2ух сред.

1)

2)

3)

4)

(В этих уравнениях -поверхностная плотность эл.зарядов, -поверхностная плотность тока проводимости на рассматриваемой границе раздела)

!!! Когда поверхностных токов НЕТ, то 4ое граничное условие переходит в

Вопрос № 26 Аналогия между магнитным и электростатическим полями.

Рассмотрим уравнения , , , ,

, , , , , .

Из них следует аналогия между векторами - электрического смещения (электрической индукции) и - магнитной индукции, а также между векторами напряженностей полей и .

Но силовыми характеристиками полей являются только и . Введение остальных двух векторов позволяет записывать уравнения в симметричном виде.

Вопрос № 27 Расчет индуктивности, взаимной индуктивности простейших устройств

Индуктивностью (коэффициентом самоиндукции) называют коэффициент пропорциональности между током и возбуждаемым им потокосцеплением. Если речь идет об отношении потокосцепления одного из двух контуров в силе обусловливающего его тока в другом контуре, то говорят о взаимной индуктивности (коэффициенте взаимной индуктивности).

Воздушные контуры

  ;

;

,

где L и M – собственная и взаимная индуктивности; di – нити тока; dl – элементы длины нитей; Ө - угол между элементами; μ₀ – магнитная постоянная.

индуктивность либо проводов простой формы, либо участков, составляющих сложные контуры. В последнем случае индуктивность контура состоит из суммы индуктивностей всех участков и двойной суммы взаимной индуктивности между участками, т.е.

 (k ≠ i),

где n – число участков.

Вопрос № 28 Метод сеток, метод конечных элементов, метод интегральных уравнений. Применение ЭВМ для расчета ЭМП.

Вопрос № 29 Уравнения Максвелла в комплексной форме. Комплексные параметры среды.

1-ое уравнение Максвелла относительно комплексных амплитуд может быть записано так:

rot= σ+jw; (1.34)

В полном виде оно записывается

rot =σ+jw; (1.35)

1.34, 1.35-1-ое уравнение Максвелла в комплексной форме.

Преобразуем уравнение 1.35 чтобы правая часть одночленной:

rot =(σ+jw) =jw (1.35a)

где:

; (1.36)

–коплексная диэлектрическая проницаемость среды, в которой распространяется ЭМП.

Преобразуем уравнение 1.36, введя обозначения.

tgδ=; (1.37)

– тангенс угла диэлектрических полей.

Физически он означает соотношение между амплитудами токов производимости и тока смещения.

Тогда 1.36 с учетом 1.37 Записывается

; (1.38)

Если tgδ=0, то - действительная величина в этом случае потерь распространении нет.

Уравнение 1.36 и 1.38 записываются еще в другой форме

Формула (1.39)

Tgδ= (1.40)

-абсолютная диэлектрическая проницаемость вакуума. 

2 Второе уравнение Максвелла

Записывается в виде

rot (1.41)

В общем случае магнитные материалы обладают потерями. В этом случае

=-j

характеризует потери в магнитных средах.

где =4π* - абсолютная магнитная проницаемость не магнитных материалов и сред.

3 Полная система уравнений Максвелла в комплексной форме имеет вид:

rot= jw; (1.42а)

div=-jw; (1.42б)

div=; (1.42в)

div=0; (1.42г)