
- •Вопрос № 1. Основные понятия электромагнитного поля. Определение силы действующей на заряд в электрическом и магнитном поле.
- •Вопрос № 4. Принцип непрерывности электрического тока и магнитного потока в интегральной форме.
- •Вопрос № 5. Безвихревой характер поля. Потенциал и градиент потенциала (напряженность), их определение с помощью теоремы Гаусса для системы заряженных тел.
- •Вопрос № 22 Аналогия между электрическим полем в проводящей среде и электростатическим полем в диэлектрике.
- •Вопрос № 30 Электромагнитные волны и излучение. Волновое уравнение и его решение.
- •Вопрос № 33 Энергия электромагнитного поля. Вектор Пойнтинга. Баланс мощности в замкнутой области пространства.
Вопрос № 5. Безвихревой характер поля. Потенциал и градиент потенциала (напряженность), их определение с помощью теоремы Гаусса для системы заряженных тел.
Из
условия
![]() следует
одно важное соотношение, а именно,
величина,
векторного
произведения
следует
одно важное соотношение, а именно,
величина,
векторного
произведения
![]() для
стационарных электрических полей всегда
равна нулю.
для
стационарных электрических полей всегда
равна нулю.
Величина
![]() ,
называется
ротором
или
вихрем
и
обозначается, как rot E.
,
называется
ротором
или
вихрем
и
обозначается, как rot E.
Мы получаем важнейшее уравнение электростатики:
|
|
rot E. |
(3.5.1) |
|
Таким образом кулоновское электростатическое поле – безвихревое.
Потенциал
![]() –
энергетическая характеристика ЭСП, в
данной точке поля равная отношению
–
энергетическая характеристика ЭСП, в
данной точке поля равная отношению
 (14)
(14)
где
![]() –
потенциальная энергия пробного заряда
–
потенциальная энергия пробного заряда
![]() ,
помещенного в данную точку ЭСП.
,
помещенного в данную точку ЭСП.
В
поле точечного
заряда потенциал
точки, находящейся на расстоянии
![]() от
заряда:
от
заряда:
 ,
(15)
,
(15)
где
![]() –
заряд, создающий поле.
–
заряд, создающий поле.
Потенциал связан с напряженностью ЭСП следующим соотношением:
![]() ,
(18)
,
(18)
где
![]() –
вектор градиента потенциала.
–
вектор градиента потенциала.
Проекция
вектора напряженности
![]() на
направление вектора градиента потенциала
на
направление вектора градиента потенциала
 (19)
(19)
Здесь
![]() –
модуль градиента потенциала.
–
модуль градиента потенциала.
В однородном ЭСП, в котором вектор напряженности одинаков во всех точках поля, модуль напряженности
 ,
(20)
,
(20)
где
![]() –
потенциалы точек двух эквипотенциальных
поверхностей;
–
потенциалы точек двух эквипотенциальных
поверхностей;
![]() –
расстояние между этими поверхностями
по нормали к ним, т. е. вдоль силовой
линии ЭСП.
–
расстояние между этими поверхностями
по нормали к ним, т. е. вдоль силовой
линии ЭСП.
расчета
напряженности
![]() электростатического
поля:
электростатического
поля:
С помощью теоремы Гаусса – по формуле
Теорема Гаусса для ЭСП в вакууме:
 (9),
(9),
для
полей, обладающих симметрией (сферической,
осевой или зеркальной). Для таких полей
метод позволяет найти функцию
![]() –
зависимость напряженности
–
зависимость напряженности
![]() от
расстояния от центра (оси) симметрии
поля.
от
расстояния от центра (оси) симметрии
поля.
Вопрос № 6. Закон электромагнитной индукции в интегральной форме.
Представим, существует переменное во времени магнитное поле в некоторой области пространства. Далее рассмотрим произвольный замкнутый контур L, при положении мгновенной направленности векторов B указано на рисунке стрелками.

Тенденция обхода контура L вдоль которого выбрано против часовой стрелки, то есть если же наблюдать с конца вектора B. Закон электромагнитной индукции в интегральной форме располагает следующим математическим выражением:

Вопрос № 7. Закон полного тока в интегральной форме.
Количественная
связь между циркуляцией вектора
![]() по
замкнутому контору и током внутри
контура определяется законом полного
тока в интегральной форме:
по
замкнутому контору и током внутри
контура определяется законом полного
тока в интегральной форме:
![]() (17.3)
(17.3)
Линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, пронизывающему замкнутый контур.
Интегральную
форму закона полного тока применяют,
когда может быть использована симметрия
в поле.

![]() .
(17.4)
.
(17.4)
Вопрос № 8. Уравнение электромагнитного поля в дифференциальной форме (уравнение Максвелла).

Вопрос № 9. Закон электромагнитной индукции в дифференциальной форме.
дифференциальная форма закона электромагнитной индукции:

Следовательно, в соответствии рассматриваемого закона, изменение во времени магнитного поля несёт в себе возникновение в пространстве электрического поля.
Вопрос № 10. Теорема Гаусса и Постулат Максвелла в дифференциальной форме.
Теорема Гаусса и постулат Максвелла в дифференциальной форме записи имеют вид:
![]()
или в иной форме:
![]() ,
,
где r -объемная плотность электрического заряда в данной точке пространства. Выражение, стоящее в левой части уравнения, называется расхождением или дивергенцией вектора напряженности или электрического смещения.
Вопрос № 11. Принцип непрерывности электрического тока и магнитного потока в дифференциальной форме.
Дифференциальная форма записи уравнения непрерывности записывается так:
|
|
|
Магнитный поток – это поток вектора магнитной индукции через некоторую поверхность:
 (17.9)
(17.9)
Соотношение
(17.9) можно трактовать как дифференциальную
форму принципа непрерывности магнитного
потока. В любой точке магнитного поля
нет ни истока, ни стока линий вектора
магнитной индукции. Линии вектора
![]() нигде
не прерываются, они представляют собой
замкнутые сами на себя линии.
нигде
не прерываются, они представляют собой
замкнутые сами на себя линии.
Вопрос № 12. Основные понятия и уравнения электростатического поля. Уравнения Пуассона и Лапласа.
Уравнения Пуассона и Лапласа являются основными дифференциальными уравнениями электростатики.
![]()
Это дифференциальное уравнение носит название уравнения Пуассона.
Интеграл
![]()
является решением уравнения Пуассона для случая, когда заряды распределены в конечной области пространства.
Если в рассматриваемой области пространства отсутствуют объемные электрические заряды, то уравнение Пуассона получает вид
![]() и
называется в этом частном случае
уравнением
Лапласа.Оператор
?2
часто обозначают
и
называется в этом частном случае
уравнением
Лапласа.Оператор
?2
часто обозначают
![]() и
называют оператором Лапласа или
лапласианом.
и
называют оператором Лапласа или
лапласианом.
Вопрос
№ 13. Расчет электростатического поля
бесконечно длинного заряженного цилиндра
из диэлектрического материала.
Решение:
б) в любой точке пространства напряженность электрического поля направлена перпендикулярно оси цилиндра, и её модуль зависит только от расстояния до этой оси:
![]()
в) В
качестве поверхности интегрирования
S
выберем цилиндр радиуса r
произвольной высоты h
(рис.5.4). Это обусловлено тем, что в каждой
точке боковой поверхности данного
цилиндра Er(r)=const
(при r=const),
а поток вектора
![]() через
верхнее и нижнее донышки цилиндра равен
0. Последнее же связано с тем, что в каждой
точке этих донышек
через
верхнее и нижнее донышки цилиндра равен
0. Последнее же связано с тем, что в каждой
точке этих донышек
![]() и,
следовательно,
и,
следовательно,
![]() ).
имеем:
).
имеем:
 ,
,
Здесь Q - заряд, попавший внутрь поверхности интегрирования.
г) Найдём напряжённость поля внутри и вне цилиндра.
Заряд, попавший внутрь цилиндра радиуса r и высоты h равен (см. рис.5.4)

и мы имеем
 При
рассмотрении внешней области внутрь
поверхности интегрирования попадает
Q=h.
Следовательно
При
рассмотрении внешней области внутрь
поверхности интегрирования попадает
Q=h.
Следовательно
 д) Таким
образом, напряженность поля данного
цилиндра в каждой точке пространства
определяется выражением:
д) Таким
образом, напряженность поля данного
цилиндра в каждой точке пространства
определяется выражением:
|
|
|
Вопрос № 14. Расчет электростатического поля двух заряженных проводов.
Ответ в методичке ПЗ 25.
Вопрос № 15. Расчет емкости и напряженности электрического поля двух заряженных проводов.
Ответ в методичке ПЗ 26.
Вопрос
№ 16-17.
Расчет
поля двухпроводной линии, если радиус
провода соизмерим с расстоянием между
проводами.

Вопрос № 18. Метод зеркальных изображений.
Для расчета электростатических полей, ограниченных какой-либо проводящей поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя диэлектриками, широко применяют метод зеркальных изображений.
Устраним мысленно проводящую среду и заменим ее проводом, являющемся зеркальным изображением реального провода в поверхности раздела и имеющим заряд реального провода, но противоположного знака (рис. 1.33). Действительный провод и его зеркальное изображение составляют двухпроводную линию. Поле от такой системы заряженных проводников (рассмотрено в примере 9 раздела 1.14) в области над проводящей средой останется таким же, как и в действительных условиях.
В этом и заключается метод зеркальных изображений.
 Поле
в любой точке нижнего полупространства
определяют как поле от дополнительного
провода, имеющего линейную плотность
заряда t3
и расположенного в той же точке, где
находился действительный проводник. В
этом случае, не только нижнее, но и
верхнее полупространство заполняется
диэлектриком с диэлектрической
проницаемостью e3
(рис. 1.34, в).
Поле
в любой точке нижнего полупространства
определяют как поле от дополнительного
провода, имеющего линейную плотность
заряда t3
и расположенного в той же точке, где
находился действительный проводник. В
этом случае, не только нижнее, но и
верхнее полупространство заполняется
диэлектриком с диэлектрической
проницаемостью e3
(рис. 1.34, в).
Линейная плотность t2 и t3 зарядов дополнительных проводников определяется с помощью следующих соотношений:
![]()
Вопрос № 19 Группы формул уравнений Максвелла. Потенциальные коэффициенты, коэффициенты электростатической индукции, частичные емкости в системе заряженных тел.
Вопрос № 20 Поле и емкость двухпроводной и трехфазной линии электропередачи с учетом влияния земли.
Вопрос № 21 Электрическое поле постоянного тока, его уравнения, граничные условия.
Уравнения электрического поля в дифференциальной форме имеют вид:
|
|
(1) |
|
|
(2) |
|
|
(3) |
На
поверхности раздела сред, где
![]() ,
Eс
или
,
Eс
или
![]() изменяются
скачком, справедливы следующие
соотношения:
изменяются
скачком, справедливы следующие
соотношения:
E1t - E2t = E1сt - E2сt
т.е. скачок тангенциальной составляющей вектора напряженности электрического поля равен скачку сторонней тангенциальной составляющей вектора напряженности электрического поля. Если Eс = 0, то тангенциальная составляющая векторного поля E непрерывна на любой поверхности раздела сред.
![]()
т.е.
скачок нормальной составляющей плотности
тока проводимости равен скачку нормальной
составляющей сторонней плотности тока
с противоположным знаком. Если
![]() =
0, то нормальная составляющая плотности
тока проводимости непрерывна на любой
поверхности раздела сред.
=
0, то нормальная составляющая плотности
тока проводимости непрерывна на любой
поверхности раздела сред.


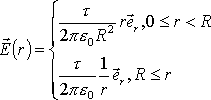 (5.9)
(5.9)