3 Статистический анализ системы случайных величин

3.1 Для выявления зависимости между входным сопротивлением транзистора и коэффициентом усиления усилителябыло обследовано 60 транзисторов. Результаты испытаний приведены в таблице 10.

Таблица 10 – Исходные данные испытаний коэффициента усиления усилителя

Номер измерения			Номер измерения
1	0,88	6,05	13	0,84	6,28
2	0,78	6,38	14	0,74	6,61
3	0,61	6,56	15	0,78	6,89
4	0,98	7,12	16	1,18	7,39
5	0,88	6,68	17	0,66	6,01
6	0,89	6,44	18	0,85	6,59
7	0,77	6,10	19	0,76	6,71
8	0,88	6,98	20	0,89	6,22
9	1,05	7,31	21	0,50	6,03
10	0,96	6,64	22	0,94	6,88
11	0,84	6,77	23	0,91	6,64
12	1,08	7,05	24	0,62	6,00

Продолжение таблицы 10

Номер измерения			Номер измерения
25	0,69	6,37	43	0,97	7,00
26	0,91	6,55	44	0,84	6,49
27	0,81	6,90	45	0,82	6,73
28	0,83	6,70	46	0,91	6,99
29	0,77	6,25	47	0,77	6,59
30	0,77	6,44	48	0,78	6,61
31	1,09	6,98	49	0,82	6,88
32	0,83	6,28	50	0,93	6,77
33	0,91	6,77	51	0,84	6,49
34	0,76	6,88	52	0,88	6,98
35	1,01	6,71	53	0,89	6,55
36	0,87	6,45	54	0,97	6,81
37	0,74	6,28	55	0,71	6,71
38	0,99	6,99	56	0,64	6,41
39	0,74	6,71	57	0,92	6,88
40	0,65	6,50	58	0,83	6,99
41	0,82	6,79	59	0,88	6,63
42	0,72	6,46	60	0,92	6,84

3.2 Определим минимально необходимое число наблюдений, обеспечивающих получение результата статистического анализа с заданной доверительной вероятностью.

Минимально необходимое число наблюдений определяется по формуле

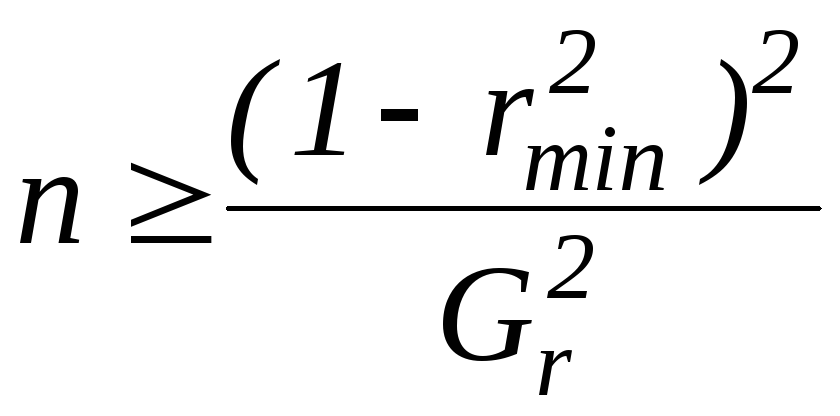, (18)

где - минимальное значение коэффициента корреляции, начиная с которого корреляционная связь признается практически достоверной;

- средняя квадратичная ошибка оценки коэффициента корреляции, определяемая по формуле

; (19)

- гарантированный коэффициент, определяемый на основании таблицы функций Лапласа и равный отношению половины ширины доверительного интервалак среднему квадратичному отклонению.

Примем минимальное значение коэффициента корреляции, равным = 0,25. Вероятность попадания случайной величиныв доверительный интервалравна

. (20)

Из последнего выражения определяется значение функции Лапласа на основании заданной доверительной вероятности. Примем значение доверительной вероятности, равное 0,95, тогда функция Лапласа будет равна

.

По таблицам функций Лапласа (таблица П.Б.1) находится ее аргумент, который и равен гарантированному коэффициенту . В данном случае

.

Следовательно, средняя квадратичная ошибка оценки коэффициента корреляции и минимально необходимое число наблюденийбудут равны

;

.

Имеющаяся в наличии таблица испытаний обеспечивает минимально необходимое количество наблюдений.

3.3 Определим размах варьирования по каждой переменной

; (21)

= 1,18 – 0,5 = 0,68;

; (22)

= 7,39 – 6,0 = 1,39.

Для каждой переменной зададим число интервалов, равное семи. Тогда ширина интервала для каждой переменной будет равна

; (23)

. (24)

С учетом этого запишем в корреляционную таблицу граничные значения интервалов переменных.

Далее произведем замену переменных, которые определим по формулам

; (25)

, (26)

где - соответственно середины интервалов величини;

- соответственно середины интервалов величини, которые обычно выбирают в середине интервального ряда в качестве условного нуля;

- соответственно ширина интервалов величини.

В качестве условного нуля приняты = 0,85 и= 6,7 – середины интервалов переменных, которые находятся в серединах интервальных рядов. Новые переменные, вычисленные по вышеприведенным формулам, также вносятся в корреляционную таблицу вместе с исходными переменными.

3.4 Корреляционную связь между случайными величинами целесообразно проводить в форме корреляционной таблицы, которая для данного случая представлена в таблице 11.

Таблица 11 – Корреляционная таблица анализа коэффициента усиления усилителя

									my	myy'	my(y')2
		-3	-2	-1	0	1	2	3
		0,5 ÷ 0,6	0,6 ÷ 0,7	0,7 ÷ 0,8	0,8 ÷ 0,9	0,9 ÷ 1,0	1,0 ÷ 1,1	1,1 ÷ 1,2
-3	6,0÷6,2	1	2	1	1				5	-15	45
-2	6,2÷6,4		1	3	3				7	-14	28
-1	6,4÷6,6		3	3	6	1			13	-13	13
0	6,6÷6,8			5	6	4	1		16	0	0
1	6,8÷7,0			2	5	7	1		15	15	15
2	7,0÷7,2					1	1		2	4	8
3	7,2÷7,4						1	1	2	6	18
									60	-17	127
		1	6	14	21	13	4	1	60	
		-3	-12	-14	0	13	8	3	-5	
		9	24	14	0	13	16	9	85	
		-3	-11	-10	-10	8	6	3	-	-
		9	22	10	0	8	12	9	70	

3.5 По данным корреляционной таблицы рассчитаем коэффициент корреляции по формуле

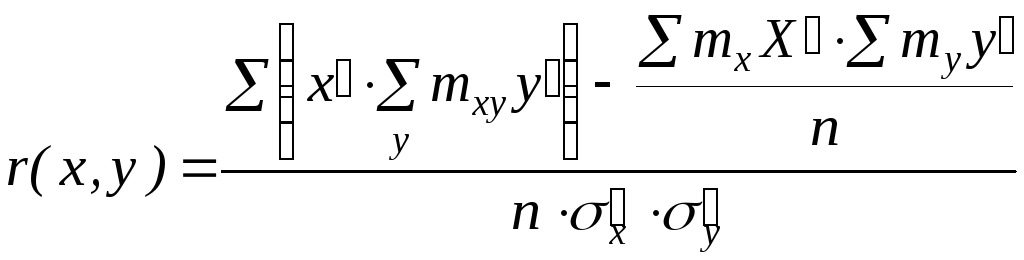, (27)

где - число испытаний, в приведенном выше примере= 60;

- соответственно средние квадратичные отклонения величини, определяемые по формулам

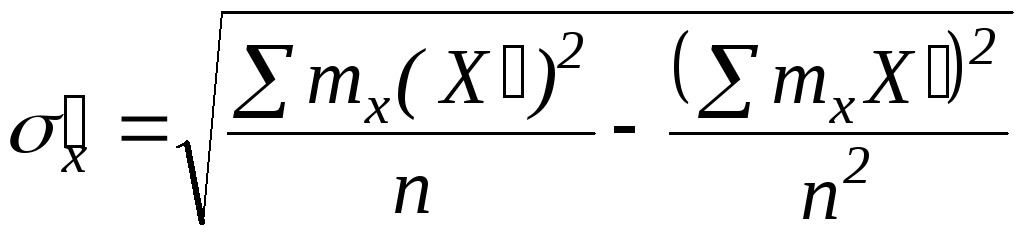; (28)

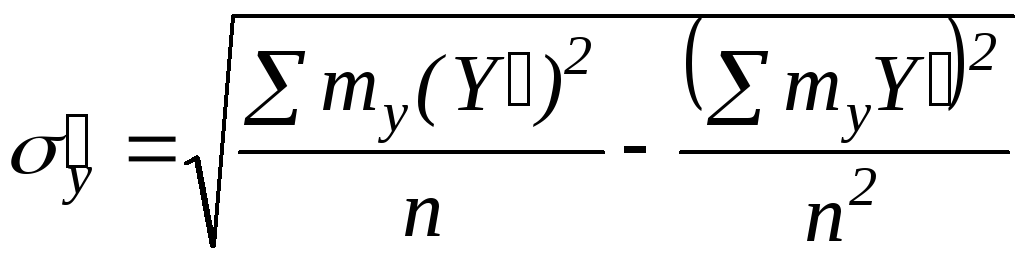. (29)

Для данного примера находим

;

,

тогда коэффициент корреляции по формуле (27) будет равен

.

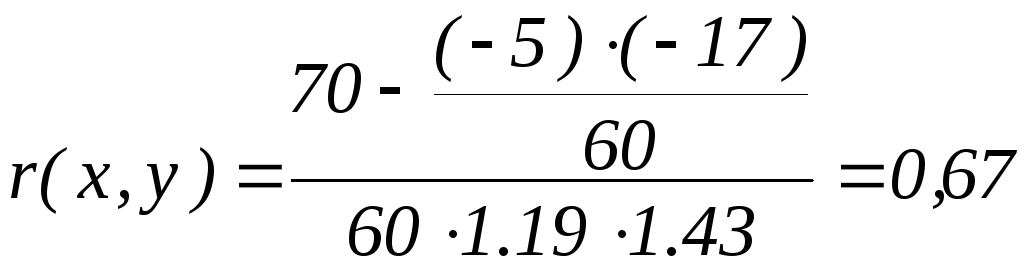Так как , то между входным сопротивлением транзистора и коэффициентом усиления усилителя имеет место определенная корреляционная связь.

Определим реальные значения среднеквадратичных отклонений входного сопротивления и коэффициента усиления по формулам

; (30)

. (31)

Для данного примера они равны

;

.

3.6 Среднее значение величины при изменении величиныи среднее значение величины при изменении величины определяются с помощью следующих формул:

; (32)

; (33)

;

.

3.7 По полученным данным рассчитаем коэффициенты уравнения регрессии с помощью следующих формул:

; (34)

; (35)

;

.

Следовательно, для коэффициента усиления уравнение линейной регрессии будет иметь следующий вид:

; (36)

.

Определим номинальное значение коэффициента усиления , для этого в уравнение регрессии подставим, тогда

. (37)

3.8 Рассчитаем погрешность коэффициента усиления, для этого продифференцируем вышеприведенное уравнение регрессии, получим

. (38)

Значение определим как наибольшее отклонение от среднего его значения

,

следовательно,

;

.

Результирующее значение коэффициента усиления с учетом погрешности запишем в виде

; (39)

.