5.9 Адсорбция из раствора на границе с газом

Термодинамический анализ состояния поверхностного слоя раствора на границе с газом позволяет выяснить влияние поверхностного натяжения раствора и термодинамической активности растворенного вещества на ве­личину адсорбции. Впервые такую зависимость нашел Гиббс:

, (V.32)

где a - термодинамическая активность;

 - поверхностное натяжение раствора на границе с газом;

d/da - изменение поверхностного натяжения раствора при беско­нечно малом изменении термодинамической активности.

Для разбавленных растворов (для которых ) уравнение (V.32) принимает вид:

, (V.33)

где С - концентрация раствора.

Это наиболее употребительная форма уравнения Гиббса. При этом надо помнить, что выражение (V.33) применимо только для сильно разбавленных раство­ров. С увеличением концентрации раствора активность компонента все в большей степени может отличаться от концентрации, а это может привести к появлению экстремума на изотерме адсорбции.

Величина g = – d/dС называется поверхностной активностью растворенного вещества для разбавленных растворов.

Выясним, влияет ли природа растворенного вещества на его адсорбцию?

По отношению к воде (в дальнейшем будем в качестве растворителя ис­пользовать воду) различают поверхностно-активные (ПАВ), поверхностно-инактивные (ПИАВ) и безразличные вещества.

ПАВ - это вещества, добавление которых уменьшает поверхностное натя­жение воды. К ним относятся дифильные вещества, молекулы которых состо­ят из радикала и полярной функциональной группы (например, R-COOH , R-NH₂ , R-OH и т.д.). Условно ПАВ обозначают так . Кружочком обозначают функциональную группу, а черточкой - углеводородный радикал.

ПИАВ – это вещества, добавление которых увеличивает поверхностное на­тяжение воды. К таким веществам относятся неорганические электролиты (минеральные кислоты, щелочи, соли).

Безразличные вещества - это вещества, добавление которых не влияет на величину поверхностного натяжения. Так ведут себя сахара.

Проанализируем вид изотермы в зависимости от природы растворенного вещества.

1. При растворении ПАВ с увеличением его концентрации  раствора уменьшается (рис. V.27, кривая 1), следовательно, -d/dc>0 и величина ад­сорбции во всей области концентрации положительна (рис. V.28, кривая 1). Растворенное ПАВ стремится из объема раствора перейти на поверхность, при малой концентрации ПАВ ведет себя как двухмерный газ (имеет две степени свободы, рис. V.29а), а при значительной концентрации образует конденсированную пленку (рис. V.29б). Достигается максимальная величина адсорбции Г_max, которая на единице поверхности будет равна:

Г_max = 1/(N_AS_o),

где S_o- площадь, занимаемая одной молекулой ПАВ (точнее ее полярной группой) в насыщенном монослое;

N_A - число Авогадро.

Отсюда

S_o=1/(Г_max N_A). (V.34)

При адсорбции ПАВ-гомологов с увеличением их концентрации величина адсорбции вначале возрастает до некоторого значения Г_max (часто обоз­начают Г_), а затем остается неизменной. Существенно то, что у гомо­логов Г_max одинакова, так как в предельном случае образования конденсиро­ванной пленки (рисунок 7б) в поверхностном слое может располагаться оди­наковое количество молекул гомологов, хотя они отличаются величиной не­полярного углеводородного радикала.

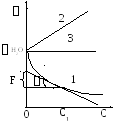
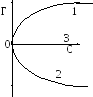
Рисунок V.28 – Изотерма адсорбции различных веществ на границе раствор-газ

Рисунок V.27 – Изотерма поверхностного натяжения при растворении различных веществ в воде

2. При добавлении ПИАВ с повышением его концентрации (C) поверхностное натяжение раствора увеличивается (рис. V.27, кривая 2), поэтому -d/dС<0, а величина ад­сорбции во всей области имеет отрицательную величину (Г < 0) (рис. V.28, кривая 2), т.е. идет десорбция - ПИАВ стремится с поверхности уйти в объем раствора.

3. Растворение безразличных веществ не влияет на величину  раствора (рис. V.27, кривая 3), т.е. d /dС = 0 и Г = 0, следовательно, безразличные вещества не адсорбируются на границе раздела фаз раствор- газ (рис. V.28, кривая 3).

Рассмотрим подробнее адсорбцию ПАВ.

Для построения изотермы адсорбции ПАВ на границе раздела жидкость -газ необходимо знать значения d/dС. Если экспериментально изучена зависимость  = f (С) и построена изотерма поверхностного натяжения (рис. V.27, кривая 1), то графически путем проведения касательных к точ­кам, соответствующих концентрациям C, легко определить поверхност­ную активность G (рис. V.27), а затем рассчитать величину адсорбции Г. Например, для концентрации C₁:

(V.35)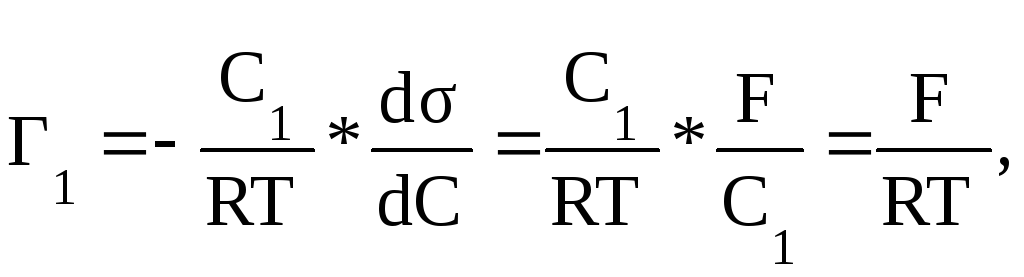

где F -отрезок, заключенный между точкой пересечения касательной с осью , при C=0 (значениев точке касания).

Рисунок V.29 – Поведение растворенного ПАВ в поверхностном слое в зависимости от концентрации

а б

Поверхностная активность зависит как от химического строения моле­кулы ПАВ, так и от природы растворителя. Дюкло, а затем Траубе устано­вили, что поверхностная активность предельных жирных кислот в водном растворе при температурах, близких к комнатной, возрастает в их гомоло­гическом ряду на каждую группу -CH₂ в среднем в 3,2 раза. Эта законо­мерность названа правилом Траубе и в подавляющих случаях соблюдается для адсорбции различных гомологов из водных растворов.

Таким образом, изотермы адсорбции различных жирных кислот-гомологов будут иметь вид, представленный на рисунке V.30.

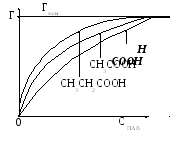
Рисунок V.30 – Изотермы адсорбции жирных кислот

Анализ уравнения Гиббса показывает, что для построения изотермы ад­сорбции необходимо знать закономерность изменения поверхностного натя­жения раствора от концентрации ПАВ. Такую закономерность можно устано­вить экспериментально, однако надо помнить о трудоемкости и необходи­мой тщательности проведения такого эксперимента. Часто при построении изотерм поверхностного натяжения в широкой области концентрации ПАВ пользуются эмпирическим уравнением Шишковского:

 =_o- B ln (1+KС), (V.36)

где , _o - поверхностное натяжение растворителя и раствора с кон­центрацией ПАВ;

B - константа для всех гомологов, учитывающая площадь, занимае­мую полярной группой ПАВ в конденсированной пленке;

K -константа, характеризующая взаимодействие молекул ПАВ друг с другом в сплошном монослое и меняется в гомологическом ряду в соответствии с правилом Траубе.

Часто константы В, К в уравнении Шишковского заменяют на a и b:

 =_o- a ln (1+bС). (V.36a)

Для больших концентраций растворов, когда Kc>>1, уравнение (12) можно привести к линейному виду:

_o -  =  =B ln K + B ln c. (V.37)

Измерив поверхностное натяжение раствора ПАВ всего лишь нескольких концентраций (не менее двух) в области больших концентраций, можно гра­фически (рис. V.31) найти константы B и K , а затем рассчитать как , так и Г для любой концентрации раствора.

Рисунок V.31 – Графическое нахождение констант уравнения Шишковского

Ленгмюр, используя уравнение Шишковского, привел уравнение Гиббса (V.37) к виду:

G=G Kc/(1+KС), (V.38)

где G=B/(RT).

Уравнение (V.38) легко привести к линейному виду, решив его относительно либо С/G, либо 1/G:

C/G = 1/G_maxK + C/ G_max , (V.39)

1/G = 1/ G_max KC + 1/G_max , (V.40) (16)

а затем графически (рис. V.37) найти константы уравнения (V.36).

Для построения графиков (рис. V.30, V.31) достаточно двух-трех значений, рассчитанных по уравнению (V.35) по данным изотермы поверхност­ного натяжения (рис. V.27) при С < 0,1.

9. Адсорбция из раствора на твердой поверхности

Адсорбция из раствора на твердом теле является практически наиболее распространенной, так как является основным методом разделения смесей и очистки производственных растворов от смесей.

Адсорбция из раствора более сложна по сравнению с адсорбцией из га­зовой фазы тем, что здесь явление сильно усложняется наличием третьего компонента – растворителя, который является конкурентом при адсорбции рас­творенного вещества.

В зависимости от степени взаимодействия растворенного вещества с растворителем различают молекулярную и ионную адсорбции из раствора на твердом теле.