5.8.7 Теория полимолекулярной адсорбции бэт

(Брунауэра, Эммета, Теллера)

Основные положения теории:

1. Адсорбция многослойна, так как вызывается физическими силами. Молекулы из газовой фазы могут адсорбироваться поверх уже адсорбиро­ванных молекул. Первый слой адсорбата удерживается в результате меж­молекулярного адгезионного взаимодействия разнородных молекул, второй и последующие слои – путем обычной конденсацией пара (газа).

2. Для простоты считают, что когезионное взаимодействие между мо­лекулами адсорбата отсутствует.

3. Процесс адсорбции находится в динамическом равновесии с про­цессом десорбции.

Эти положения позволили получить уравнение изотермы полимолеку­лярной адсорбции:

A =, (V.26)

C = e^{-(Q -L)/*R*T},

где A_, A –величина адсорбции максимальная и при равновесном давлении Р;

P_o - давление насыщенного пара;

C – константа;

Q_адс, L – теплоты адсорбции в монослое и конденсации пара (газа).

Теория рассматривает процесс присоединения первой молекулы адсорбтива активным центром, как адсобцию, а присоединение всех остальных молекул, как конденсацию паров. Константа адсорбции С = К_адс/К_конд = const.

К_адс характеризует образование первого слоя, К_конд – образование всех последующих слоев.

Если С < 2, малая чистая теплота адсорбции, то уравнение БЭТ описывает изотерму адсорбции типа III (рис. V.10).

Если С > 2, большая чистая теплота адсорбции, то уравнение БЭТ описывает S-образную изотерму типа II (рис. V.10).

Если С> 1, а Р/Р_s мало, то уравнение переходит в уравнение Ленгмюра.

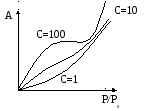
Рисунок V.20- Виды изотерм адсорбции по теории БЭТ

Анализ уравнения БЭТ

1. При малых значениях давления (P/P_o1) уравнение переходит в уравнение Ленгмюра, т.е. описывается изотермой I типа (рис. V.10).

2. С увеличением давления при С > 0 уравнение описывает изотер­мы II типа, при С < 0 -III типа (рис. V. 10).

На изотерме адсорбции (рис. V.10 кривые II,III) точка перегиба соответствует окончанию заполнения моно­слоя на твердой поверхности и началу заполнения второго слоя адсор­бента.

Решение уравнения БЭТ

Уравнение БЭТ имеет и другую форму записи:

V =, (V.27)

где V, V_m – объем, который занимают молекулы адсорбированного вещества на всей поверхности адсорбата и в монослое;

Уравнение изотермы БЭТ позволяет определить величину адсорбции(V), ем­кость монослоя (V_m), удельную поверхность (S_уд) адсорбента (порошков, пористых адсорбентов и катализаторов).

Константы С и A находят графически (рис. V.21), для этого урав­нение БЭТ приводят к линейному виду:

= . (V.28)

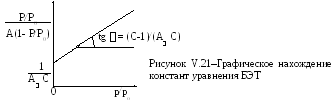
Наиболее надежные результаты величины S_уд получают, используя уравнение БЭТ при адсорбции азота (при минус 196^oС) или аргона (при минус 183^oС). При величине адсорбции A, соответствующей точке пе­региба S-образной изотермы при отношении P/P_o от 0,03 до 0,3, изотерма в координатах [(P/P_o) / A*(1-(P/P_o))] - (P/P_o) хорошо спрям­ляется.

5.8.8 Капиллярные явления. Уравнение Томсона-Кельвина .

Капиллярная конденсация

Теория БЭТ, являясь наилучшей теорией физической адсорбции, не да­ет математического описания изотерм IV и V видов (рис V.11).

Указанные типы изотерм характерны тогда, когда на физическую ад­сорбцию накладывается капиллярная конденсация пара при использовании пористых адсорбентов. Пары жидкости конденсируются в капиллярах пр адсорбции. Если данная жидкость смачивает стенки капилляра, то она образует вогнутую поверхность. Если жидкость не смачивает капилляр, то она образует вогнутый мениск. Изменение кривизны поверхности связано с изменением давления насыщенного пара над поверхностью и термодинамических свойств системы.

Рассмотрим сферу, образованную пленкой жидкости (рис.V.22).

Капиллярное давление ΔР можно представить в виде:

ΔР = ( 2 σ_жг /r) cos Θ.

Чем меньше радиус капли, тем больше давление внутри нее. В капле воды с радиусом 10^-6 см относительное давление равно 50 .

Давление над вогнутым мениском (рис. 24) уравновешивается весом столба жидкости высотой h в капилляре. С учетом веса столба жидкости

( 2 σ_жг /r) cos Θ = (ρ – ρ_о)gh,

где ρ и ρ_о - соответсвенно плотности жидкости и воздуха.

В связи с тем, что ρ >> ρ_о последней величиной можно пренебречь. Высоту подъема жидкости в капилляре определяют по формуле:

h = 2 σ_жг cos Θ/ (rgρ)

При полном смачивании cos Θ = 1,

h = 2 σ_жг / (rgρ).

Так, высота поднятия воды в капилляре радиусом 10^–4 см составляет 15 м.

Зависимость давления паров от радиуса капли или мениска лежит в основе процессов рекуперации (возвращение потери паров в процесс) и изотермической перегонки жидкостей.

При температуре Т над вогнутой поверхностью с радиусом кривизны r давление конденсации пара (P_r) данной жидкости меньше, чем над плоской поверхностью (P_o), а над выпуклой поверхностью давление конденсации пара (P_r) больше, чем над плоской поверхностью (P_o). Этo явление описывается уравнением Томсона- Кельвина:

ln (P_o/P_r) = 2*q/(R*T*r), (V.29)

где q ,  - молярный объем и поверхностное натяжение жидкости.

Поэтому в результате полимолекулярной адсорбции в широких (10^-8м) порах адсорбента при больших давлениях скапливается жидкость, которая смачивает стенки капилляра, в результате чего жидкость образует вог­нутый мениск. При этом пары адсорбтива конденсируются при давлениях, меньших давления насыщенного пара над плоской поверхностью.

Для процесса капиллярной конденсации характерно существование сорбционного гистерезиса (рис. V.11, кривые IV,V). Зигмонди объяснил гистерезис тем, что при адсорбции на стенках капилляров образуются менее вогнутые мениски, чем это следовало ожидать, так как смачиванию стенок препятствует адсорбированный еще в процессе приготовления ад­сорбента воздух (или другой газ). В то время как при десорбции радиус кривизны мениска будет большим, следовательно, давление, отвечающее одному и тому же количеству поглощенной жидкости, при десорбции будет меньше, чем при адсорбции (P₂<P₁) (рис. V.23).

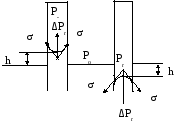
Рисунок V.23- Капиллярные явления

Нужно иметь в виду, что капиллярная конденсация наблюдается толь­ко на пористых адсорбентах и при относительно больших давлениях.

Согласно этому уравнению при смачивании жидкостью поверхности капилляра конденсация в капилляре происходит при более низком давлении, чем вне его. При несмачивании - насыщенный пар в капилляре будет конденсироваться при большем давлении, чем на плоской поверхности. Эти явления проявляются тем больше, чем больше поверхностное натяжение и меньше радиус капилляра.

Адсорбенты имеют сложную пористую структуру. Для анализа процесса адсорбции рассматривают поры трех основных видов: коническую, цилиндрическую и цилиндрическую, открытую с обоих концов.

а). При адсорбции в конической поре при малых значениях Р на стенках образуется слой жидкости со сферическим мениском. По мере заполнения поры радиус мениска растет. Это возможно только при повышении давления Р. Обратный процесс – десорбция выражается той же кривой.

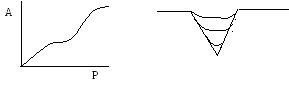
Рисунок V.24 – Адсорбция в конических порах и изотерма адсорбции

б). При адсорбции в цилиндрической поре при малых значениях Р на стенках поры образуется тонкий слой жидкости с о сферическим мениском в нижней части поры. На нем начинается капиллярная конденсация и пора заполняется жидкостью. Радиус кривизны мениска при этом не изменяется. Адсорбция и десорбция идут при постоянном давлении и выражаются одинаковой кривой.

А

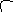
Р

Рисунок V.25 – Адсорбция в цилиндрических порах и изотерма адсорбции

в). В цилиндрической поре, открытой с обоих концов, при малых давлениях на стенках поры образуется слой жидкости с вогнутым цилиндрическим мениском. При капиллярной концентрации радиус мениска уменьшается. Конденсация происходит при постоянном давлении, и пора заполняется жидкостью. На открытых концах образуются сферические мениски, которые постепенно изменяют кривизну при повышении давления. При десорбции процесс сначала идет обратимо с поверхности сферического мениска возрастающей кривизны, а затем он идет с поверхности сферического мениска постоянного радиуса внутри поры. Поэтому испарение жидкости наблюдается при меньших давлениях по сравнению с конденсацией. На изотерме появляется петля капиллярного гистерезиса.

А

р

Рисунок V.26 – Адсорбция в цилиндрических открытых порах и изотерма адсорбции

По десорбционной части изотермы определяют радиус пор.

А.В.Киселев предложил термодинамическое уравнение капиллярной конденсации. При V,T и n_i = const dF = -δ W.

dU = -σds;

;

, (V.30)

где S – площадь поверхности твердого тела

a - удельная адсорбция

P_S – давление насыщенного пара над плоской поверхностью

P – равновесное давление пара в условиях опыта

Этим уравнением удобно пользоваться при определении площади поверхности адсорбента

Изучение теории адсорбции газа и паров на твердой поверхности по­казывает, что по типу изотермы нельзя отнести адсорбцию к моно- или полислойной. Формирование единой теории адсорбции связано, по-видимо­му, с объединением правильных взглядов различных исследователей. Соз­дание такой теории чрезвычайно актуально, так как большинство исполь­зуемых промышленностью адсорбентов и катализаторов являются пористы­ми или порошкообразными веществами.