
- •2. Источники эдс и источники тока и их внешние характеристики.
- •4. Расчет сложных электрических цепей методом уравнений Кирхгофа.
- •5. Расчет сложных электрических цепей методом контурных токов.
- •6. Расчет сложных электрических цепей методом узловых потенциалов.
- •7. Расчет параллельных электрических цепей методом двух узлов.
- •8. Параметры синусоидального тока и их отображение на временной диаграмме. Угол сдвига фаз.
- •9. Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление. Фазовые соотношения между напряжением и током.
- •10. Конденсатор в цепи переменного тока. Емкостное сопротивление. Фазовые соотношения между напряжением и током.
- •12. Изображение синусоидальных электрических величин в комплексной форме. Комплексные амплитуды и комплексы электрических величин. Векторные диаграммы электрических величин на комплексной плоскости.
- •14. Последовательная цепь r, l на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
- •15. Последовательная цепь r, c на переменном токе: векторная диаграмма тока и напряжений, треугольник напряжений. Закон Ома в комплексной форме.
- •16. Последовательная цепь r, l, c на переменном токе: векторная диаграмма тока и напряжений. Реактивное сопротивление цепи. Резонанс напряжений.
- •17. Разветвленные электрические цепи переменного тока: комплексная проводимость последовательной ветви r, l, треугольник проводимостей, эквивалентная параллельная схема с проводимостями.
- •18. Параллельная электрическая цепь из конденсатора и катушки индуктивности: эквивалентная параллельная схема, векторная диаграмма токов. Резонанс токов.
- •20. Коэффициент мощности. Повышение коэффициента мощности компенсацией сдвига фаз.
- •23. Гармонический анализ несинусоидального периодического тока: разложение в тригонометрический ряд, параметры гармоник, параметры несинусоидального тока.
- •25. Уравнения четырехполюсника в разных формах. Экспериментальное определение коэффициентов четырехполюсника формы а из опытов холостого хода и короткого замыкания.
- •26. Уравнения длинной линии с потерями в показательной форме. Коэффициент отражения.
- •27. Расчет переходных процессов классическим методом: определение независимых условий, составление характеристического уравнения его решение, определение постоянных интегрирования.
- •28. Расчет переходных процессов операторным методом: операторная схема, операторные изображения электрических величин и параметров цепей, переход к функции времени по формуле разложения.
- •30. Графические методы расчета последовательных нелинейных электрических цепей постоянного тока.
- •31. Графические методы расчета параллельных нелинейных электрических цепей методом двух узлов.
- •33. Расчет последовательной магнитной цепи.
- •34. Расчет параллельной магнитной цепи методом двух узлов.
26. Уравнения длинной линии с потерями в показательной форме. Коэффициент отражения.
Цепи
(линии электропередачи, передачи
информации, обмотки электрических машин
и аппаратов и т.д.), где электромагнитное
поле и потери равномерно или неравномерно
распределены вдоль всей цепи –
называют длинными
линиями.
Для оценки, отнести ли цепь к длинным
линиям
следует сравнить ее длину l
с длиной электромагнитной волны
![]() .
Если приf=50
Гц длинной
считается линия протяженностью >6000
км, то при f=108
Гц, линию, уже протяженностью всего лишь
>3 м, следует считать длинной.
.
Если приf=50
Гц длинной
считается линия протяженностью >6000
км, то при f=108
Гц, линию, уже протяженностью всего лишь
>3 м, следует считать длинной.
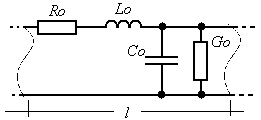
Линию с равномерным распределением вдоль линии ее параметров: индуктивности, сопротивления, емкости и проводимости, называют однородной. Линию с неравномерным распределением параметров часто можно разбить на однородные участки.
-
первичные параметры длинной линии:
![]() ,
,![]() ,
,![]() и
и![]() ;
;
- вторичные параметры длинной линии:
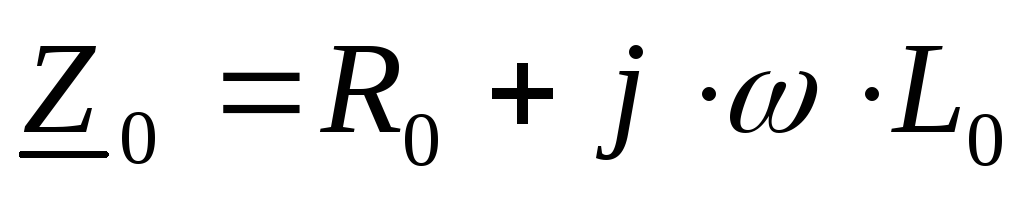 -
комплекс продольного сопротивления
длинной линии;
-
комплекс продольного сопротивления
длинной линии;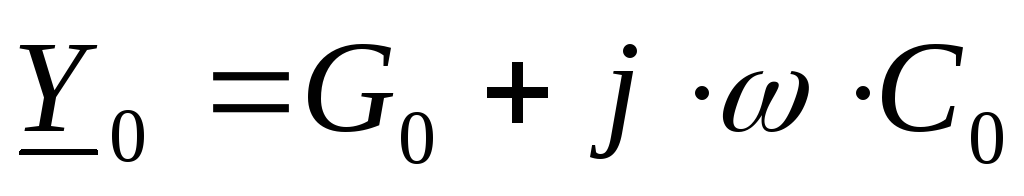 -
комплекс поперечной проводимости
длинной линии;
-
комплекс поперечной проводимости
длинной линии;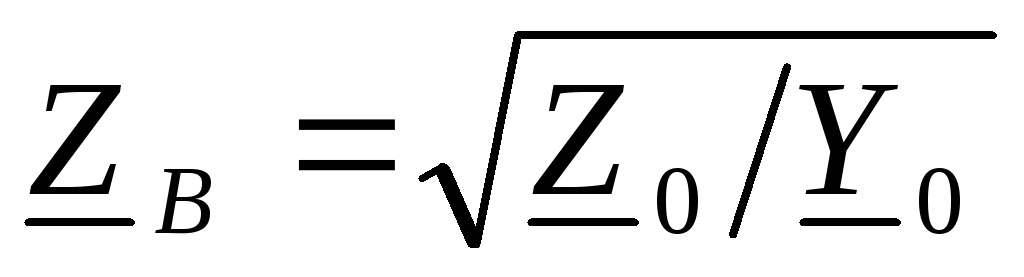 -
комплекс волнового сопротивления
длинной линии;
-
комплекс волнового сопротивления
длинной линии;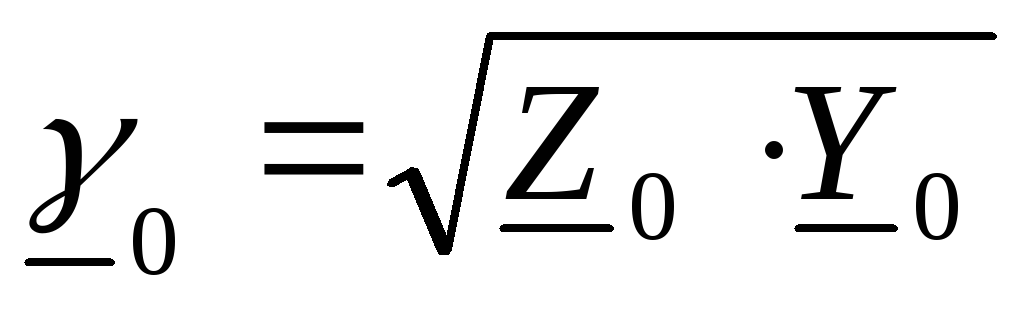 -
комплекс коэффициента распространения
эл. магн. волны;
-
комплекс коэффициента распространения
эл. магн. волны;
-
уравнение
относительно начала линии
(х=0),
постоянные
![]() и
и![]() определяем из граничных условий:х=0,
заданы ток и напряжение:
определяем из граничных условий:х=0,
заданы ток и напряжение:
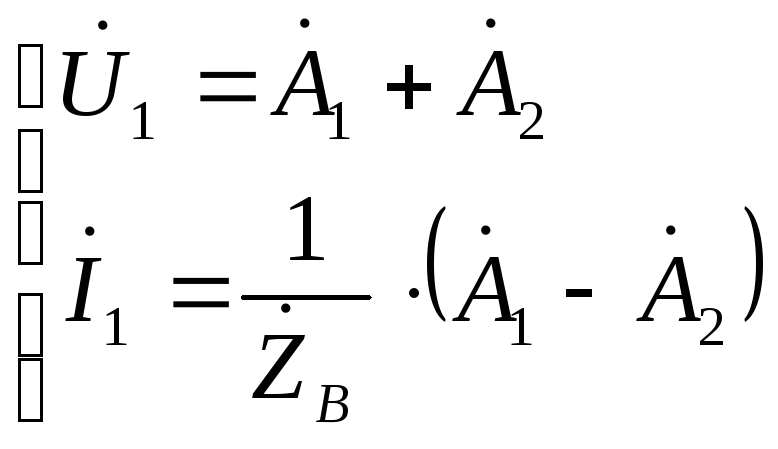
![]()
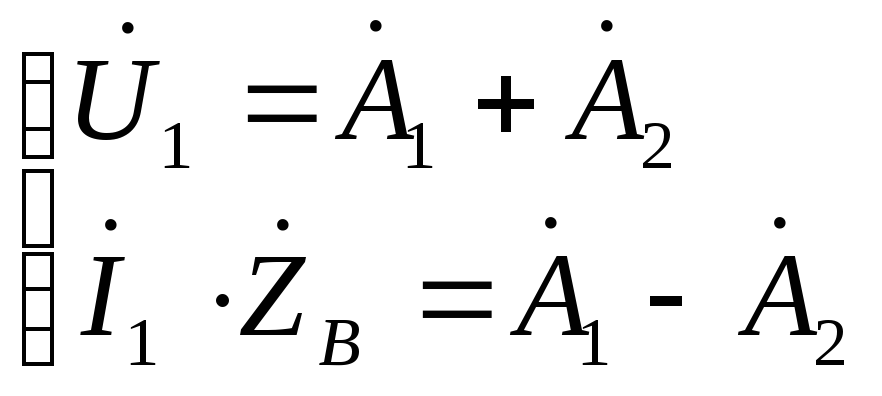
![]()
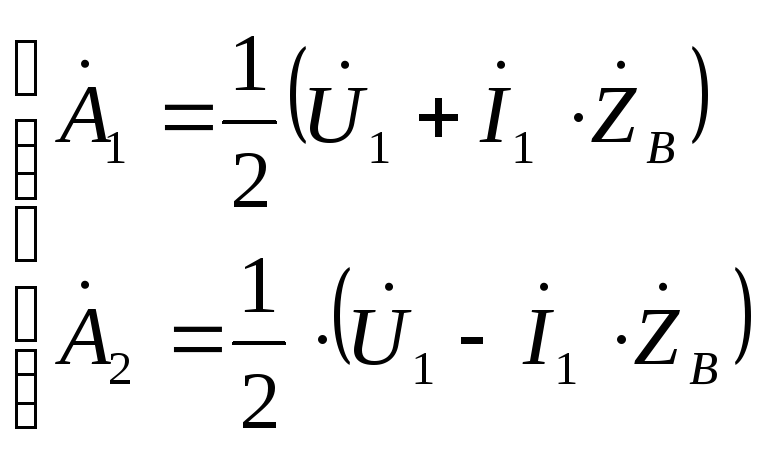
подставив
полученные постоянные
![]() и
и![]() в начальную систему, получим уравнение
относительно начала линии в показательной
форме:
в начальную систему, получим уравнение
относительно начала линии в показательной
форме:
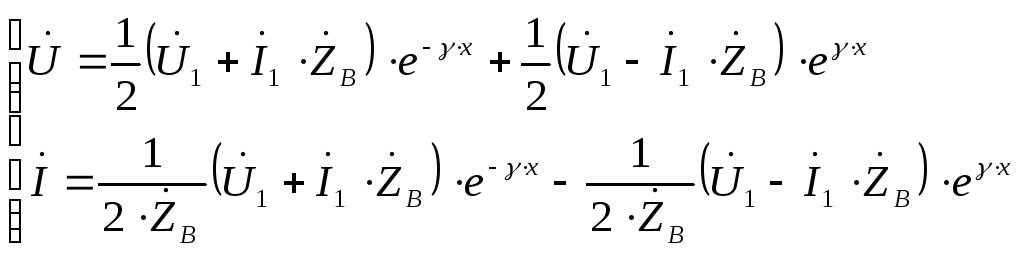
уравнение позволяет определить ток и напряжение в любой точке линии по их известным значениям в начале линии.
- уравнение относительно конца линии (длина – l, расстояние от конца линии - x)
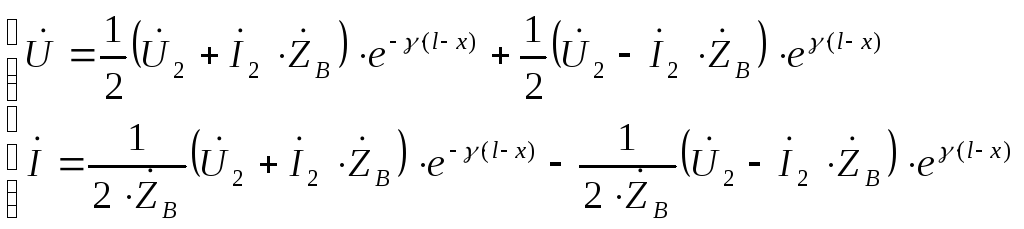
уравнение позволяет определить ток и напряжение в любой точке линии по их известным значениям в конце линии.
Для определения коэффициента отражения необходимо уравнение длинной линии с потерями относительно конца линии в показательной форме.
![]() -
для напряжения.
-
для напряжения.
Коэффициент отражения – это отношение отраженной волны с падающей волне в конце линии.
![]() -
прямая волна.
-
прямая волна.
![]() -
отраженная волна.
-
отраженная волна.
![]() -
для тока.
-
для тока.
![]() -
прямая волна
-
прямая волна
![]() -
отраженная волна.
-
отраженная волна.
Найдем коэффициент отражения, зная, что y=0 (конец линии).
Коэффициент
отражения по напряжению:
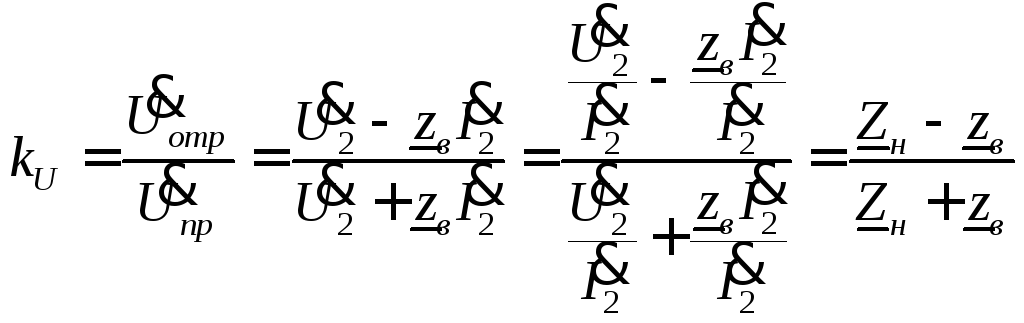
Коэффициент
отражения по току:
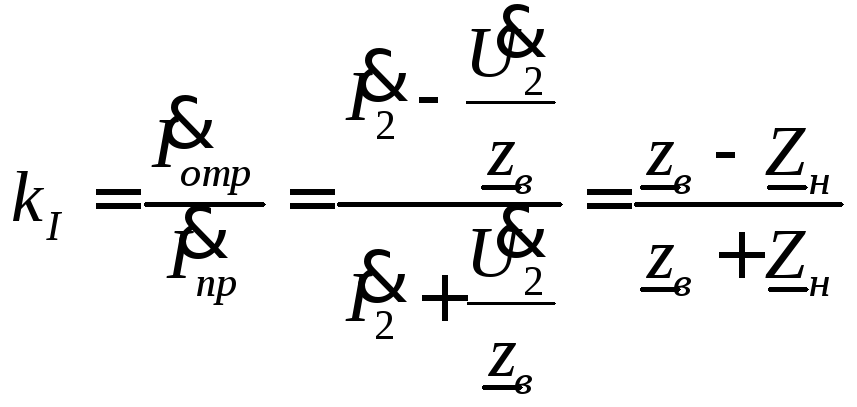
1.
если
![]() ,
то нагрузка согласованная
,
то нагрузка согласованная![]()
![]() ,
отражения нет, волна идет в нагрузку,
,
отражения нет, волна идет в нагрузку,
![]() ,
вся энергия идут потребителю
,
вся энергия идут потребителю
2.
ХХ –
разомкнутая линия,
![]() ,
,![]() - волна полностью отразилась без смены
фазы,
- волна полностью отразилась без смены
фазы,![]() ,
волна полностью отразилась со сменой
фазы.
,
волна полностью отразилась со сменой
фазы.
3.
КЗ –
замкнутая линия,
![]() ,
,![]() - волна отражается со сменой фазы,
- волна отражается со сменой фазы,![]() - волна отражается без смены фазы.
- волна отражается без смены фазы.
27. Расчет переходных процессов классическим методом: определение независимых условий, составление характеристического уравнения его решение, определение постоянных интегрирования.
- переходными называются процессы, происходящие при коммутации в эл. цепях, в которых есть реактивные элементы. Различают конфигурацию цепи до коммутации и после коммутации.
- классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе. В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в таблице:
|
Резистор (идеальное активное сопротивление) |
Катушка индуктивности (идеальная индуктивность) |
Конденсатор (идеальная емкость) |
|
|
при
наличии магнитной связи с катушкой,
обтекаемой током
|
|
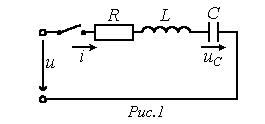
Для последовательной цепи, содержащей резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u можно записать:
![]() ;
;
Подставив в это выражение значение тока через конденсатор, получим:
![]()
линейное
дифференциальное уравнение второго
порядка относительно
![]() .
.
В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии (L и C), имеет вид:
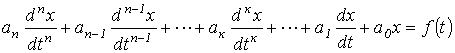
- законы коммутации:
ток в катушке индуктивности в момент коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него:
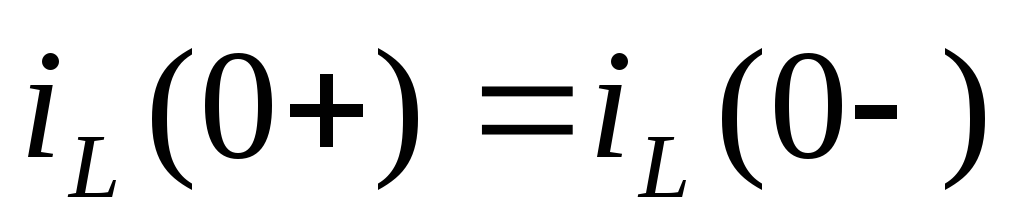 ;
;напряжение на конденсаторе в момент коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него:
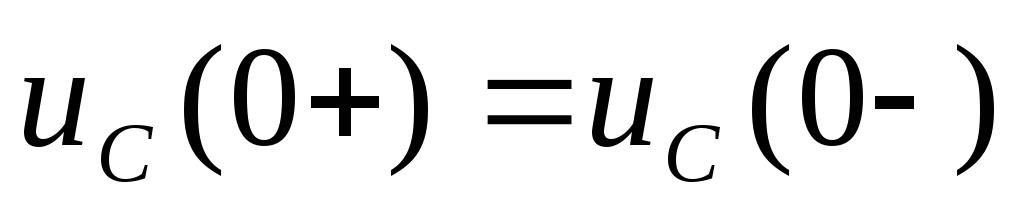 ;
;
- независимые начальные условия (определяются из докоммутационной конфигурации):
![]() -
ток в катушке индуктивности в момент
коммутации;
-
ток в катушке индуктивности в момент
коммутации;
![]() -
напряжение на конденсаторе в момент
коммутации;
-
напряжение на конденсаторе в момент
коммутации;
- в общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
запись выражения для искомой переменной в виде
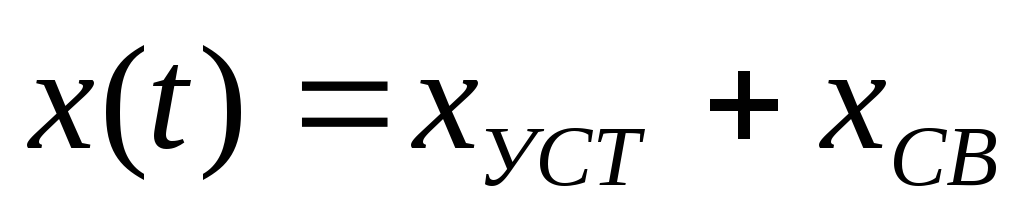 *
*нахождение установившейся составляющей из послекоммутационной конфигурации цепи.
составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени τ). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
подстановка полученных выражений установившейся и свободной составляющих в выражение *.
определение начальных условий и на их основе – постоянных интегрирования.
Пример расчета переходного процессов классическим методом
Переходные процессы в RL цепи при ее подключении к источнику постоянного напряжения
![]()
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Согласно
рассмотренной методике для тока в цепи
можно записать:
![]() ;
;
Тогда
для первого случая установившаяся
составляющая тока:
![]() ;
;
Характеристическое
уравнение:
![]() ,
откуда
,
откуда![]() и постоянная времени
и постоянная времени![]() .
Т.о.
.
Т.о.![]() .
Подставляя, запишем:
.
Подставляя, запишем:![]()
В
соответствии с первым законом коммутации
![]() .
Тогда
.
Тогда![]() ,
откуда
,
откуда![]() .
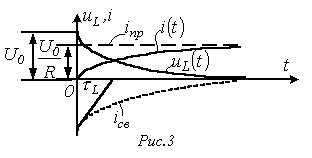
Т. о., ток в цепи в переходном процессе
описывается уравнением:
.
Т. о., ток в цепи в переходном процессе
описывается уравнением:
![]() ,
,
а напряжение на катушке индуктивности – выражением:
![]()
